|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Индивидуальные задания. КРАТКАЯ АННОТАЦИЯ МОДУЛЯ
КРАТКАЯ АННОТАЦИЯ МОДУЛЯ Модуль на тему «Статистическое изучение динамики социально-экономических явлений» разработан для дистанционного образования студентов. Этот модуль позволит им самостоятельно изучить тему и вопросы к ней, а также проверить качество усвоенного материала. В нем дается изложение учебного материала, тесты, задачи для проверки знаний и умений, указана литература, а также приведен смысл понятий, которые введены в модуль. Данный модуль знакомит студентов с задачами, решение которых дает возможность усвоить правила построения и анализа рядов динамики для характеристики изменения социально-экономических явлений во времени, выявления основной тенденции, закономерностей их развития. Достигается это соответствующей обработкой рядов динамики, анализом изменения его уровней, расчетом аналитических показателей. ОПОРНАЯ ЛЕКЦИЯ ТЕМАТИЧЕСКИЙ ПЛАН: 1. Понятие о рядах динамики, их виды и правила построения. 2. Сопоставимость уровней и смыкание рядов динамики 3. Аналитические показатели ряда динамики. 4. Средние показатели ряда динамики. 5. Сезонные колебания и статистические методы их измерения. 6. Прогнозирование на основе рядов динамики.
1. ПОНЯТИЕ О РЯДАХ ДИНАМИКИ, ИХ ВИДЫ И ПРАВИЛА ПОСТРОЕНИЯ.
Одной из главных задач статистики является исследование изменений общественных явлений во времени, поскольку они находятся в непрерывном развитии. Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Изучение динамики в статистике происходит при помощи построения рядов динамики, в которых процесс развития выступает наиболее ярко. Ряд динамики – ряд последовательно расположенных во времени статистических показателей, которые в своих изменениях отражают ход развития изучаемого явления, иначе – количественная характеристика состояния и изменения общественных явлений во времени. Ряд динамики состоит из двух элементов: 1) времени– момента (даты) или периода (год, месяц, квартал), к которым относятся статистические данные; 2) уровней ряда – статистических показателей, характеризующих состояние явления на указанный момент или период времени. Уровни ряда обычно обозначаются через «у», моменты или периоды времени, к которым относятся уровни, - через «t». Уровни ряда динамики могут быть выражены разными формами статистических показателей, и в зависимости от уровня различают ряды динамики абсолютных величин и, как производные от них, ряды средних и относительных величин. Важными условиями при построении рядов динамики являются: - достоверность уровней; - взаимосвязанность рядов динамики по существенным статистическим показателям; - последовательность и непрерывность во времени уровней ряда. Уровни ряда должны последовательно охватывать весь этап развития и, чтобы вскрыть закономерности, ряды должны быть достаточно длинными; - сопоставимость уровней ряда динамики; несопоставимость уровней возникает в результате изменения территории, даты учета, методики расчета показателей, цен, единиц измерения . По характеру изучаемого явления и длительности времени различают два вида рядов динамики: - моментный ряд - характеризует размеры явления по состоянию на определенный момент времени. Для моментного ряда характерно то, что каждый последующий уровень полностью или частично включает в себя предыдущий. - интервальный ряд - характеризует размеры показателя за определенный промежуток времени (день, месяц, год) составляют интервальный ряд. В интервальном ряду величина уровня представляет собой итог какого-либо процесса за тот или иной период (интервал времени). В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. Вид динамического ряда определяется не произвольно, а исходя из содержания изучаемого показателя. Так, по показателям, характеризующим состояние явлений, условий, факторов процесса, строятся моментные ряды (численность населения, поголовье скота, наличие техники). По показателям, отражающим итоги происходящих процессов, строят интервальные ряды (производство продукции, затраты труда). В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями во времени - ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат; с неравноотстоящими уровнями во времени - в рядах даются прерывающиеся периоды или неравномерные промежутки. В таблице 1 представлен интервальный ряд динамики абсолютных величин с равноотстоящими уровнями во времени. Уровни интервального ряда динамики могут быть суммированы, так как не содержат повторного счета. Таблица1 – Динамика Валового выпуска продукции Республики Беларусь
Примером моментного ряда абсолютных величин с неравноотстоящими уровнями во времени можно назвать ряд динамики, показывающий общую площадь жилых помещений городского жилищного фонда Республики Беларусь (таблица 2). Таблица 2 – Городской жилищный фонд Республики Беларусь, на конец года
Отдельные уровни моментного ряда динамики содержат элементы повторного счета, так как отдельные жилые помещения, учитываемые, например, в 1940 г., существуют и в настоящее время, являясь единицами совокупности и в 2014 г. Все это делает бессмысленным суммирование уровней моментных рядов динамики. При составлении рядов динамики должны выполняться следующие требования: 1. Периодизация развития, т. е. расчленение ряда во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. 2. Сопоставимость статистических данных по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. 3. Соответствие величины временных интервалов интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Соответственно, для стабильных процессов интервалы можно увеличить. 4. Упорядоченность во времени числовых уровней рядов динамики. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.
2. СОПОСТАВИМОСТЬ УРОВНЕЙ И СМЫКАНИЕ РЯДОВ ДИНАМИКИ
Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней. Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие – в квадратных метрах. На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей. Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие – с убранной, то такие уровни будут несопоставимы. В процессе развития во времени, прежде всего, происходят количественные изменения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития. Процесс выделения однородных этапов развития рядов динамики носит название периодизации динамики. Вопрос о том, какие этапы развития прошло то или иное явление за определенный исторический отрезок времени, решается теорией той науки, к области которой относится изучаемая совокупность явлений. Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл. Скажем, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое. Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных границ областей, районов и так далее. Следовательно, прежде чем анализировать динамический ряд, надо, исходя из цели исследования, убедиться в сопоставимости уровней ряда и, если последняя отсутствует, добиться ее дополнительными расчетами. Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах). ПРИМЕР. Произвести смыкание следующих динамических рядов объемов продукции фирмы (на базе цен на 1.01.2004) по данным:
РЕШЕНИЕ. Для перевода данных таблицы в сопоставимый вид в ценах 2011 г. определим коэффициент как соотношение выпуска продукции в ценах 2009 и 2011 гг.: 4300:4000=1,075. Затем данные за предшествующие изменению периоды (2009-2011), умножаем на этот коэффициент и получаем условно сопоставимые уровни в абсолютных величинах и так называемое смыкание ряда. Можно использовать и другой способ смыкания рядов динамики. Уровни переходного периода (2009г.) принимаем за 100%, а уровни других периодов, как до, так и после изменения, рассчитываются по отношению к уровню переходного периода в процентах. В результате получают сопоставимый ряд относительных величин: для 2009 г.: 2180/4000
3. АНАЛИТИЧЕСКИЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ.
Уровни ряда динамики дают общую оценку изменения исследуемого явления. А для характеристики направления и интенсивности развития исчисляются показатели ряда динамики. Абсолютное изменение уровней (абсолютный прирост, абсолютное сокращение) – это разность уровней ряда. Абсолютный прирост показывает, насколько изменился данный уровень по сравнению с предшествующим или начальным. Различают два способа расчета показателей динамики: - цепной- каждый последующий уровень сравнивается с предыдущим, - базисный - производится последовательное сравнение уровней с начальным. Поскольку базисный уровень принимается за критерий для оценки достигнутых уровней, при его выборе не должно быть формального подхода. За базу сравнения следует брать периоды, соответствующие границам качественных переходов в развитии изучаемого явления. Абсолютный прирост при базисном способе определяется как сравнение уровней с базисным уровнем. Сумма цепных абсолютных приростов равна базисному абсолютному приросту. При отрицательном значении абсолютного изменения его лучше назвать абсолютным сокращением. Анализируя динамический ряд абсолютного изменения уровней, определяем направление развития (рост, снижение), а сравнивая aбсолютные изменения последующего с предыдущим, устанавливаем характер изменения (равномерный, ускоренный, скачкообразный), т. е. определяем абсолютное ускорение. Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда. Коэффициент роста имеет большее аналитическое значение в сравнении с абсолютным приростом, т. к. дает возможность сравнивать темпы изменения любых признаков независимо от различия их материальной природы, единиц измерения и величины уровней. Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).
Таблица 3 – Методика расчета аналитических показателей ряда динамики
Темп роста – это отношение каждого последующего уровня ряда динамики к предыдущему или начальному, выраженное в процентах. Темп роста показывает, сколько процентов составляет сопоставляемый уровень к базисному или предыдущему уровню ряда динамики и позволяет определить направления и характер относительного изменения изучаемого явления. Темп прироста (относительный прирост) – отношение абсолютного прироста к предыдущему или начальному уровню ряда динамики, выраженное в процентах. Темп прироста показывает на сколько процентов (какую долю) последующий уровень выше или ниже предыдущего, и поэтому темп прироста может быть исчислен как разность между темпом роста и 100 %. На практике нельзя ограничиваться лишь исчислением темпа прироста. Надо знать, что скрывается за каждым процентом прироста, для чего определяется абсолютное значение одного процента прироста. Значение одного процента прироста определяется отношением абсолютного прироста за каждый период к темпу прироста этого периода. Расчет показателей динамики представлен в таблице 3. Таким образом, система показателей динамики включает как абсолютные, так и относительные величины. Относительные показатели в анализе необходимо сравнивать путем определения разности уровней. Эти разности получили название пунктов. При изучении динамики необходимо комплексное использование абсолютных и относительных показателей. 4. СРЕДНИЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ.
Для обобщающей характеристики ряда динамики применяются следующие средние показатели: средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста, среднее значение одного процента прироста. Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Методика расчета средних значений показателей динамики определяется видом ряда. В интервальном ряду с равными периодами времени средний уровень определяется как простая арифметическая средняя из уровней ряда:
где n – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень. Если в интервальном ряду отрезки имеют неравную длительность, то средний уровень рассчитывается по формуле средней арифметической:
Для моментных временных рядов величина среднего уровня зависит от того, как шло развитие явления в рамках интервалов, разделяющих отдельные наблюдения. Обычно считают, что в пределах каждого периода, разделяющего моментные наблюдения, развитие происходило по линейному закону. Тогда общий средний уровень находится как среднее значение из средних по каждому интервалу. Для моментного ряда с равноотстоящими моментами получаем в итоге формулу средней хронологической, вид которой определяется способом нумерации уровней. Если уровни нумеруются начиная с нуля, то средняя хронологическая имеет вид
Для моментного ряда с неравными интервалами предварительно находятся значения уровней в серединах интервалов:
а затем определяется общий средний уровень ряда
Средний абсолютный прирост (абсолютное изменение)
где n – порядковый номер последнего уровня. Если в расчетах начальный уровень ряда динамики ведется с единицы (
При цепном способе средний абсолютный прирост определяется отношением суммы абсолютных приростов на их число:
где m – число абсолютных приростов (m = n – 1). Большое значение имеет исчисление среднего темпа роста, который характеризует динамику развития явления за какой-либо период в среднем:
В расчетах среднего коэффициента роста применяется средняя геометрическая величина. Так, при базисном способе расчета
Расчеты упрощаются, если логарифмируем это выражение:
Как уже отмечалось ранее, произведение цепных коэффициентов роста равно базисному коэффициенту роста двух крайних периодов. Средний коэффициент роста при цепном способе расчета
Средний темп прироста определяется на основе среднего темпа роста как:
Среднее содержание одного процента абсолютного прироста определяется отношением среднего абсолютного прироста к среднему темпу прироста:
5. МЕТОДЫ ВЫЯВЛЕНИЯ ОСНОВНОЙ ТЕНДЕНЦИИ В РАЗВИТИИ ЯВЛЕНИЙ.
На развитие явления во времени оказывают влияние факторы различные по характеру и силе воздействия. Поэтому при анализе динамики определяют основную тенденцию (тренд) развития явлений. Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами: 1. укрупнения интервалов; 2. скользящей средней; 3. аналитического выравнивания.
Пример 2. Рассмотрим использование этих методов на данных о квартальном объеме реализованной продукции.
Таблица 4 -Динамика объема реализованной продукции
Укрупнение интервалов от квартальных до годовых (итоговая сумма), позволяет получить более наглядную тенденцию объема реализации продукции. Смысл приема заключается в том, что первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Например, ряд, содержащий данные о квартальном объеме реализации продукции, может быть преобразован в ряд годовых данных. Вновь образованный ряд может содержать либо абсолютные величины за укрупненные по продолжительности промежутки времени (эти величины получаю путем простого суммирования уровней первоначального ряда абсолютных величин), либо средние величины. При суммировании уровней или при выявлении средних по укрупненным интервалам отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается действие основных факторов изменения уровней (общая Сглаживание скользящей средней – для этого метода необходимо установить количество уровней ряда по которому будет усредняться данный динамический ряд – квартальные – 4, данные по месяцам – 12. Для нашего примера расчет состоит в определении средних величин из четырех уровней ряда.
……………………………………………………..
При сглаживании почетному числу уровней скользящая средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания. Для нашего примера с четырьмя уровнями, скользящая средняя будет находиться между вторым Если при сглаживании рядов динамики количество уровней ряда составляется из нечетного числа уровней, то необходимость в центрировании отпадает. На рисунке 1 видна тенденция возрастания объема реализации продукции c центрированными скользящими средними.
Рисунок 1
Аналитическое выравнивание – заключается в том, что основная тенденция развития ряда динамики рассчитывается как функция времени Подбор эмпирических формул состоит из 2х этапов: - выбор вида функции дающей наилучшее приближение; - определение параметров выбранной функции. Наиболее часто применяются следующие виды функций: - линейная - параболическая - экспоненциальная - полулогарифмическая - гиперболическая - степенная Полиномы невысоких степеней имеют конкретную интерпретацию рядов динамики. Например, для линейной и параболической функций коэффициенты модели можно интерпретировать следующим образом: a0 – характеризует средние условия ряда динамики; a1 – скорость роста ряда динамики; a2 – ускорение ряда динамики. Существует правило выбора степени полинома, основанное на определении величин конечных разностей уровней ряда динамики. Согласно этому правилу полином первой степени (линейная функция) применяется в том случае, если первые разности (абсолютные приросты) постоянны, полином второй степени – когда постоянны вторые разности и т. д. Для выбора экспоненциальной функции необходима стабильность цепных темпов роста.
Если возрастание одной величины приводит к убыванию другой, то используют гиперболическую или степенную функции, а если с возрастанием одной величины наблюдается замедленное возрастание другой, то используют полулогарифмическую функцию. Аналитическое выравнивания ряда динамики по гиперболической функции для нашего примера дало следующие оценки параметров a0=408,6 и a0= -268,6. Эта зависимость представлена графически (рисунок 2).
Рисунок 2
6. ПРОГНОЗИРОВАНИЕ НА ОСНОВЕ РЯДОВ ДИНАМИКИ
При анализе временных рядов в экономике обычно предполагается, что наблюдения упорядочены во времени и разделены равными интервалами времени. Согласно одной из традиционных моделей экономические временные ряды содержат четыре компоненты: тренд, сезонное изменение, циклическое изменение и случайную компоненту. Эти компоненты необходимо определить и этот процесс называется декомпозицией. Эти четыре компоненты представляют в виде мультипликативной или аддитивной модели в зависимости от того Под сезонными колебаниями понимается устойчивое колебание ряда динамики, повторяющееся через определенные периоды времени в течение года. Циклическая компонента отличается от сезонной тем, что она имеет большую временную протяженность и отражает цикл деловой активности. Задачей статистики является выявление этих колебаний и их измерение. Наличие сезонных колебаний можно выявить на построенном графике. Измеряются сезонные колебания при помощи показателей, называемых индексами сезонности. Их расчет может быть произведен следующим образом. Пусть имеется ряд динамики
Затем находим средние значения индивидуальных индексов сезонностей по формуле.
где
Используя полученные средние значения индексов сезонностей, очищают исходный ряд динамики от сезонной составляющей, получая тренд.
Затем определяют теоретические значения тренда Для осуществления прогноза может быть использована следующая модель
Пример 3.В предыдущем примере, мы рассмотрели получение центрированных скользящих средних. Воспользуемся данным примером и продолжим расчеты индексов сезонности и других показателей с целью получения функции для прогноза, исследуемого динамического ряда. Необходимые расчеты сведем в таблицу.
Таблица 4 -Расчет индексов сезонности и прогноза
Во вспомогательной таблице представлены расчеты средних индексов сезонности.
Таблица 5 -Расчет средних индексов сезонности
Аналитическое сглаживание тренда
Рисунок 3
На следующем рисунке 4 представлены наблюдаемые квартальные данные объема реализации продукции и их ретроспективный и перспективный прогноз с учетом средних индексов сезонности,
Рисунок 4 Для выделения циклической компоненты из полученного результата
СПИСОК ЛИТЕРАТУРЫ 1. Елисеева, И.И., Юзбашев, М.М. Общая теория статистики: учебник /И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – 5-е изд., переработ. и доп. – М: Финансы и статистика, 2005. – 655с. 2. Ефимова, М.Р. Общая теория статистики: учеб. / Ефимова, М.Р., Петрова, Е.В., Румянцев, В.Н. – 2-е изд., испр. и доп. – М: ИНФРА-М, 2009. –412с. 3. Теория статистики: учебник / Шмойлова Р.А. [и др.]; под общ. ред. Р.А. Шмойловой. – 4-е изд., перераб и доп. – М: Финансы и статистика, 2005. – 655с. 4. Общая теория статистики: Учеб.-практ. пособие / Л.А. Сошникова, В.А. Тарловская, И.Н. Терлиженко и др.; под. ред. И.Н. Терлиженко. – Мн.: БГЭУ, 2004. 134с 5. Практикум по теории статистики / Р.А. Шмойлова, В.Г. Минашкин, И.А. Садовникова [и др.], под ред. Шмойловой Р.А. – 2-е изд. перераб. и допол. – М.: Финансы и статистика. 2005. -416. 6. Практикум по теории статистики: Учеб.пособие / Под ред. Р.А. Шмойловой. – М:Финансы и статистика. 2002. – 416с. 7. Статистика. Методические указания./ Сост. Т.М. Шаройкина. – Минск.: НО ООО «БИП-С». 2003 – 62 с. 8. Статистика: Учебно-методическое пособие / С.С. Захорошко. –Минск: НО ООО «БИП-С», 2002. -62 с. 9. Цыганов В.А. Общая теория статистики: Учебно-методическое пособие / В.А. Цыганов. – Минск: НО ООО «БИП-С», 2006.- 152с. 10. Цыганов В.А. Статистика промышленности. Учебно-методическое пособие/ В.А. Цыганов. – Минск: НО ООО «БИП-С», 2006.- 168с.
ФОРМЫ КОНТРОЛЯ Контрольные вопросы 1. С какой целью проводится анализ рядов динамики? 2. Какие виды рядов динамики вы знаете? 3. Каким образом происходит выявление основной тенденции ряда динамики? 4. Что является составными элементами ряда динамики? 5. Допускается ли суммирование уровней моментного ряда? 6. Что является важнейшим условием правильности построения ряда динамики? 7. Какие причины вызывают несопоставимость уровней ряда динамики? 8. Какие показатели используются для характеристики изменения уровней ряда динамики? 9. Какие средние характеристики ряда динамики вы знаете? 10. Как называется разность между последующим и предыдущим уровнями ряда? 11. Как называется отношение последующего уровня ряда к предыдущему? 12. Какая тенденция может наблюдаться в социально - экономических рядах? 13. Как называется тенденция изменения связи между отдельными уровнями? 14. Для чего предназначен метод простой скользящей средней? 15. Какие уравнения используются для отображения основной тенденции ряда динамики? 16. С помощью чего могут быть описаны сезонные колебания в ряду динамики? 17. Какое явление составляет теоретическую основу использования прогнозирования на основе рядов динамики ? 18. Какие методы относятся к простейшим методам экстраполяции? ТЕСТОВЫЕ ЗАДАНИЯ 1. Статистические ряды динамики – это: а) ряд единиц совокупности, расположенных в порядке возрастания или убывания варьирующего признака; б) ряды абсолютных величин; в) показатели, характеризующие процесс развития общественного явления во времени; г) ряды, где значения варианты даны в виде интервалов.
2. Ряды динамики классифицируют по следующим признакам: а) по способу выражения уровней ряда; б) по расстоянию между уровнями ряда; в) в зависимости от периода времени; г) по расстоянию между изучаемыми объектами.
3. Смыкание рядов динамики – это… а) обеспечение равнозначности анализируемых показателей; б) сопоставление двух или нескольких несопоставимых рядов во времени и пространстве; в) объединение в один более длинный ряд двух или нескольких несопоставимых рядов; г) обеспечение сопоставимости изучаемых признаков.
4. При расчете показателей динамики на постоянной базе сравнения… а) каждый уровень ряда сравнивается с предыдущим уровнем ряда; б) каждый уровень ряда сравнивается с последующим уровнем ряда; в) каждый уровень ряда сравнивается с одним и тем же уровнем ряда; г) каждый уровень ряда сравнивается с начальным уровнем ряда.
5. При расчете показателей динамики на переменной базе сравнения… а) каждый уровень ряда сравнивается с предыдущим уровнем ряда; б) каждый уровень ряда сравнивается с последующим уровнем ряда; в) каждый уровень ряда сравнивается с одним и тем же уровнем ряда; г) каждый уровень ряда сравнивается с начальным уровнем ряда.
6. К показателям, характеризующим тенденцию динамики относятся… а) темп роста, темп прироста, темп наращивания, абсолютный прирост; б) темп роста, темп прироста, темп наращивания, темп ускорения; в) темп прироста, темп наращивания, темп роста ускорения; г) абсолютный прирост, темп прироста, темп наращивания, темп роста ускорения.
7. Средний уровень ряда определяется по следующим формулам: а) по средней арифметической; б) по средней геометрической; в) по средней арифметической взвешенной; г) по средней хронологической.
8. Средний абсолютный прирост определяется по следующим формулам:
9. Средний темп роста определяется по следующим формулам:
10. К основным методам выявления основной тенденции развития относится… а) метод аналитического выравнивания; б) метод скользящей средней; в) метод укрупнения интервалов; г) метод средней хронологической взвешенной.
11. Если для развития явления характерны стабильные цепные абсолютные приросты, то… а) используется парабола второго порядка; б) выбирается уравнение линейного тренда; в) применяется показательная функция; г) применяется полулогарифмическая кривая.
12. Если для развития явления характерны стабильные цепные темпы прироста, то… а) используется парабола второго порядка; б) выбирается уравнение линейного тренда; в) применяется показательная функция; г) применяется полулогарифмическая кривая.
13. Если для развития явления характерны стабильные цепные темпы роста, то… а) используется парабола второго порядка; б) выбирается уравнение линейного тренда; в) применяется показательная функция; г) применяется полулогарифмическая кривая.
14. Если для развития явления характерно сокращение абсолютных цепных приростов, то… а) используется парабола второго порядка; б) выбирается уравнение линейного тренда; в) применяется показательная функция; г) применяется полулогарифмическая кривая.
15. Экстраполяция – это… а) определение последующих уровней ряда динамики на основе логического предположения дальнейшего развития явления; б) определение последующих уровней ряда динамики на основе исследования изменчивости явления; в) определение последующих уровней ряда динамики на основе фактически выявленной закономерности развития явления; г) определение последующих уровней ряда динамики на основе абстрактных заключений о закономерности развитии явления. 16. Моментные динамические ряды – это: а) процесс развития общественного явления во времени; б) ряд количественных показателей, характеризующих данное явление на определенные даты; в) ряд количественных показателей, характеризующих данное явление за определенный промежуток времени; г) ряд относительных величин.
17. Темп роста – это: а) разность между уровнями двух сравниваемых периодов; б) отношение уровня одного периода к уровню предшествующего периода; в) отношение абсолютного прироста к темпу роста; г) отношение абсолютного прироста к уровню того периода, с которым производится сравнение.
18. Средний темп роста определяется по формуле: а) б) в) г)
19. Абсолютное значение 1% прироста – это: а) отношение уровней двух периодов; б) отношение абсолютного прироста к темпу прироста; в) отношение абсолютного прироста к уровню того периода, с которым сравнивают; г) разность между уровнями двух периодов. 20. Система показателей динамического ряда включает: а) средний уровень ряда, дисперсию; б) цепные и базисные индексы, темп прироста; в) абсолютное значение 1% прироста, темп роста, темп прироста, абсолютный прирост; г) базисный абсолютный прирост, коэффициент вариации, темп роста. Индивидуальные задания В целях обеспечения многовариантности заданий, введен параметр k, который соответствует последней цифре зачетной книжки студента. Задание 1.Произвести смыкание следующих динамических рядов объемов продукции фирмы ( на базе цен на 1.01.2008) по данным:
Задание 2.На основании статистических данных Республики Беларусь за период 1995 – 2014 гг., проанализировать динамику показателя (определяется в соответствии с последней цифрой зачетной книжки).
Для выполнения задания необходимо определить цепным и базисным способами следующие показатели:
Расчеты выполнить в таблице
Задание 3.Используя взаимосвязь показателей динамики определите уровни ряда динамики и недостающие в таблице базисные показатели динамики по следующим данным о производстве часов за 2006 – 2014 гг.
Задание 4.Используя данные, приведенные ниже, определите индексы сезонности для измерения сезонных колебаний товарооборот.
Задание 5. На основе данных о дневной выработке изделий А заводом за 15 дней месяца нужно произвести сглаживание ряда методом скользящей средней (по 5 дням).
7. На основании следующих данных произвести выравнивание ряда динамики по прямой.
Поиск по сайту: |
 100%=54,5%; для 2010 г.: 3200/4000
100%=54,5%; для 2010 г.: 3200/4000 

















 , (9.1)
, (9.1) . (9.2)
. (9.2) (9.3)
(9.3) (9.4)
(9.4) (9.5)
(9.5)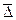 показывает, на сколько в среднем за единицу времени изменяется уровень ряда по сравнению с предыдущим. При базисном способе расчета определяется по формуле
показывает, на сколько в среднем за единицу времени изменяется уровень ряда по сравнению с предыдущим. При базисном способе расчета определяется по формуле , (9.6)
, (9.6) ), то средний абсолютный прирост определяется как:
), то средний абсолютный прирост определяется как: (9.7)
(9.7) (9.8)
(9.8) (9.9)
(9.9) (9.10)
(9.10)
 . (9.11)
. (9.11) . (9.12)
. (9.12) . (9.13)
. (9.13)


 и третьем
и третьем  уровнями. Чтобы ликвидировать этот сдвиг применяется способ центрирования. Центрированная скользящая средняя определяется из двух смежных скользящих средних, для отнесения полученного уровня к определенной дате в нашем случае к третьему кварталу 1-го года, например
уровнями. Чтобы ликвидировать этот сдвиг применяется способ центрирования. Центрированная скользящая средняя определяется из двух смежных скользящих средних, для отнесения полученного уровня к определенной дате в нашем случае к третьему кварталу 1-го года, например 

 .
. ;
; ;
; ;
; ;
;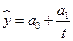 ;
;


 с временным интервалом равным одному месяцу или одному кварталу. Количество лет должно быть не менее трех. Имея эти данные, определяем скользящие средние
с временным интервалом равным одному месяцу или одному кварталу. Количество лет должно быть не менее трех. Имея эти данные, определяем скользящие средние  , если необходимо производим центрирование
, если необходимо производим центрирование  . После этого определяем индивидуальные индексы сезонности по формуле.
. После этого определяем индивидуальные индексы сезонности по формуле. (9.14)
(9.14) (9.15)
(9.15) – количество периодов, по которым рассчитывается индивидуальные индексы сезонности.
– количество периодов, по которым рассчитывается индивидуальные индексы сезонности. (9.16)
(9.16) по приведенным выше функциям от времени.
по приведенным выше функциям от времени. (9.17)
(9.17)

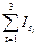

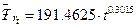 представлено на рисунке 3
представлено на рисунке 3
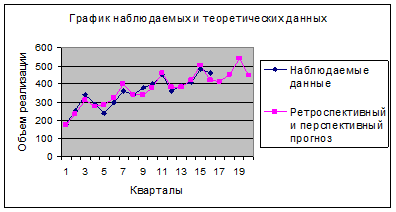
 исключают случайную компоненту с помощью трехчленного сглаживания,
исключают случайную компоненту с помощью трехчленного сглаживания,

 ;
; ;
; ;
; .
.