 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Бесконечно малые и бесконечно большие величины. Их сравнение
Определение 2.6 .Функция называется бесконечно малой (б.м.) при x → a, если
Зная определение предела функции при y=f(x)- б.м. при x → a
Обычно для обозначения бесконечно малых используют малые греческие буквы. Рассмотрим свойства бесконечно малых функций. Определение 2.6 .Функция называется бесконечно большой (б.б.) при x → a, если
Теорема 2.5 (свойства бесконечно малых).Справедливы следующие свойства 1О. Сумма конечного числа бесконечно малых есть бесконечно малая т.е. если α1(x), α2(x),… ,αn(x) – бесконечно малые при x → a , то β(x)= α1(x) + α2 (x)+… + αn(x) тоже бесконечно малая при x → a 2О. Произведение бесконечно малой и ограниченной функций есть бесконечно малая т.е. если. α(x) - бесконечно малая при x → a, а f(x) ограниченная в точке а,то β(x)=f(x)· α(x) тоже бесконечно малая при x → a. 3О. Функция обратная к бесконечно малой есть бесконечно большая т.е. если α(x) - бесконечно малая при x → a, то β(x)=1/ α(x) бесконечно большая при x → a. Доказательство приведенных свойств проводится примерно по одной схеме с использованием определений. Для примера докажем свойство 2О. Пусть фиксировано произвольное положительное число |f(x)| < M для всех х: |x-a| < В силу того, что . α(x) - бесконечно малая, по числу
Положим
Отсюда с учетом произвольности Доказательство остальных свойств полезно выполнить самостоятельно в качестве упражнения. Приведенные свойства будем использовать в дальнейшем для доказательства свойств пределов. Теорема 2.6 (свойства бесконечно больших).Справедливы следующие свойства 1О. Сумма конечного числа бесконечно малых есть бесконечно малая т.е. если α1(x), α2(x),… ,αn(x) – бесконечно большие при x → a , то β(x)= α1(x) + α2 (x)+… + αn(x) тоже бесконечно большая при x → a 2О. Функция обратная к бесконечно большой есть бесконечно малаят.е. если α(x) - бесконечно большая при x → a, то β(x)=1/ α(x) бесконечно малая при x → a.
Теорема 2.7 (о представлении функции, имеющей предел) . Для того, чтобы существовал
необходимо и достаточно, чтобы f(x) =A + a(x) (1) для некоторой б.м. при x → a функции a(x). Доказательство. Необходимость. Пусть
Достаточность условия (1) сразу следует из определения предела. Сравнение бесконечно малых функций. Символы о и О. Определение 2.7. Б.м.функции ά(x) и β(x) называются эквивалентными при
Эквивалентность ά(x) и β(x) обозначают: a ~ β , Например, в дальнейшем буде показано, что при a,→0 Sin a ~ a, tg a ~ a, ln(1+a) ~ a. Определение 2.8. Б.м.функцию ά(x) называют бесконечно малой более высокого порядка, чем β(x) (обозначается ά(x)=o( β(x)) ), если
Определение 2.9. Б.м.функцию ά(x) называют бесконечно малой одного порядка с β(x) (обозначается ά(x)=О( β(x)) ), если существует такое число С ≠ 0, что
Поиск по сайту: |
, можно дать развернутое определение бесконечно малой величины:
и пусть 
и М- какие-нибудь числа из определения ограниченности f(x) такие, что
найдется 
такое, что
для всех х: |x-a| < 
, тогда для всех х:|x-a| < 
имеем
бесконечно малая при x → a.
(*)
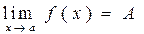
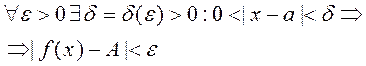, если
