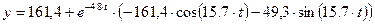|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчет переходного процесса в гидромеханической системе с учетом сжимаемости жидкости
КУРСОВАЯ РАБОТА Динамика и регулирование гидро- и пневмосистем Статический расчет и расчет переходных процессов в гидромеханической системе
Пояснительная записка КР.ДРГПС.ГПА05.69.ПЗ Вариант 1.13
Проект выполнил ________________ В. А. Мошонкин
Руководитель проекта к.т.н., доцент _________________ А. И. Квашнин
Пермь 2008 Содержание
1 Исходные данные
2 Статический расчет гидромеханической системы
2.1 Определение скорости выходного элемента гидродвигателя без учета гидравлических потерь
2.2 Определение скорости выходного элемента гидродвигателя с учетом гидравлических потерь
3 Расчет переходного процесса в гидромеханической системе без учета сжимаемости жидкости
4 Расчет переходного процесса в гидромеханической системе с учетом сжимаемости жидкости
Список использованных источников
Исходные данные.
Исходные данные для напорного трубопровода:
Плавный поворот потока на 90 град: 3 на 3 тр.;
Исходные данные для сливного трубопровода:
Исходные данные для схемы с гидродвигателем вращательного движения:
2 Статический расчет гидромеханической системы.
2.1. Определение скорости выходного элемента гидродвигателя без учета гидравлических потерь.
Условия равенства давления в начальном и конечном сечении трубопроводов соответствуют движению рабочей жидкости в гидросистеме без учета гидравлических сопротивлений, когда справедливы соотношения:
где
Движущий момент принимается равной моменту сопротивления:
где
где
Момент трения исполнительного органа
Уравнения (1), (2) и (3) решаем относительно давления
где
Получаем
Расход гидродвигателя без учета объёмных потерь в напорном трубопроводе равен расходу дросселя:
где
Принимаем минеральное масло И-50А плотностью равной
Найдем численное значение расхода гидродвигателя
=============================================!!!! Угловая скорость вращения
где
Получаем
2.2 Определение скорости выходного элемента гидродвигателя с учетом гидравлических потерь.
Таблица 1
Расчеты сведены в таблицу 1.
Запишем уравнение Бернулли относительно сечений 1-1 и 5-5 для напорного трубопровода, а также относительно сечений 6-6 и 9-9 для сливного трубопровода.
Уравнение Бернулли относительно сечений 1-1 и 5-5:
где
Пренебрегаем разностью геометрических высот, и выражаем разность пьезометрических высот:
Учтём уравнение неразрывности.
тогда уравнение Бернулли будет иметь вид:
Сумма, заключенная в квадратную скобку, является приведенным коэффициентом сопротивления
Найдем чему равен Коэффициент сопротивления для внезапного поворота на третьем участке:
Тогда
Коэффициент сопротивления для внезапного расширения на первом участке:
Коэффициент сопротивления для внезапного расширения на втором участке:
Коэффициент внезапного сужения на третьем участке:
Рисунок 1 – Напорный трубопровод
Рисунок 2 – Сливной трубопровод
Тогда
Уравнение Бернулли относительно сечений 6 – 6 и 9 – 9 сливного трубопровода (рис. 3):
где а Пренебрегаем разностью геометрических высот и выражаем разность пьезометрических высот:
Учтём уравнение неразрывности.
тогда уравнение Бернулли будет иметь вид:
Сумма, заключенная в квадратную скобку, является приведенным коэффициентом сопротивления
Найдем чему равен
Коэффициент внезапного сужения на седьмом участке:
Коэффициент сопротивления для внезапного расширения на восьмом участке:
Тогда
Найдем коэффициенты сопротивления напорного
где
Тогда
Определим потери давления.
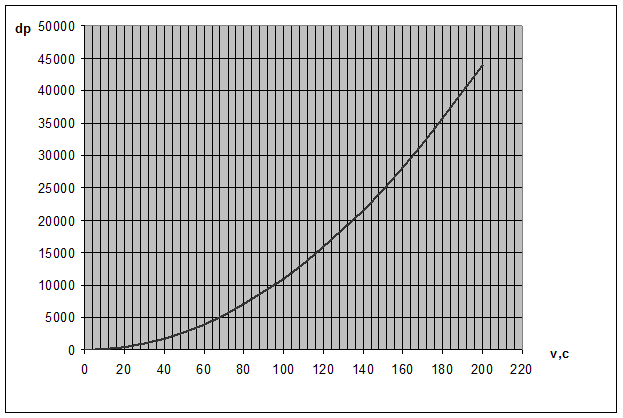
Рис.3-График зависимости потерь в напорном трубопроводе от скорости выходного элемента.
Чтобы найти
Подставим в уравнение со (*)
Проверка:
3 Расчет переходного процесса в гидромеханической системе без учета сжимаемости жидкости.
Запишем уравнение движения выходного элемента гидродвигателя для гидромотора:
Тогда уравнение примет вид
Из уравнения расхода выразим
Найдем приведенный момент инерции
Тогда
Подставим все значения в уравнение движения выходного элемента гидродвигателя для гидромотора:
И приведем к виду:
Таблица 2
Рисунок 4- График переходного процесса в гидромеханической системе при ступенчатом изменении расхода и без учета сжимаемости жидкости.
Время переходного процесса определяем по графику (Рис. 4) – время достижения установившегося значения скорости выходного элемента гидродвигателя. На графике это время фиксируется в момент вхождения кривой в пятипроцентное отклонение от установившегося значения скорости:
Расчет переходного процесса в гидромеханической системе с учетом сжимаемости жидкости.
Для упрощения математической модели линеаризуется нелинейная зависимость суммарных потерь давления в напорной и сливной гидролинии от скорости выходного элемента гидродвигателя.
Таблица 3
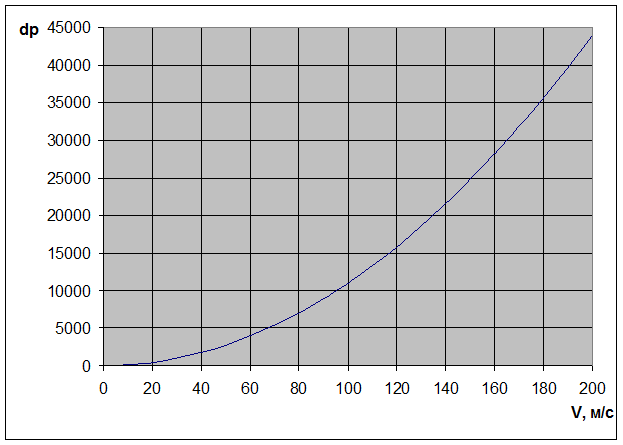
Рис.4- График зависимости суммарных потерь давления от скорости выходного элемента гидродвигателя
Для линеаризации расходной характеристики определим коэффициент расхода дросселя:
Линеаризованное уравнение расходной характеристики, полученной из разложения в ряд Тейлора
Уравнение расхода с учетом сжимаемости жидкости:
Определим
Определим суммарный объем напорного трубопровода:
Из уравнения движения
Запишем это выражение с учетом линеаризованных соотношений:
Определим первую производную давления
Подставим полученные выше выражения в уравнение расхода с учетом сжимаемости жидкости:
Упростим выражение выше, принимая:
Получили
И приведем к виду неоднородного дифференциального уравнения второго порядка с правой частью: где
Уравнение (*) приводим к виду: где
Определим коэффициенты
При
Тогда:
Таблица 4
Строим график переходного процесса в гидромеханической системе при ступенчатом изменении расхода сжимаемой жидкости (рис. 5). Этот график представляет собой колебательный затухающий процесс с учетом сжимаемости рабочей жидкости и демпфированием колебаний.
Рис.5 - График переходного процесса в гидромеханической системе при ступенчатом изменении расхода сжимаемой жидкости.
Список использованных источников:
1. Свешников В.К. Станочные гидроприводы: Справочник: Библиотека конструктора. – 4-е изд. перераб. и доп. – М.: Машиностроение, 2004. – 512с.: ил.
2. Квашнин А.И. Статический и регулирование гидро- и пневмосистем. Статический расчет и расчет переходных процессов в гидромеханической системе: учеб.-метод. пособие / А.И. Квашнин. – Пермь: Изд-во Перм. гос. техн. ун-та, 2007.- 28 с.
3. Механика жидкости. Гидравлические машины и основы гидропривода агрегатов ракетных комплексов/ Ю. М. Орлов. – Министерство обороны РФ – Пермь: Пермский военный институт ракетных войск. Пермь, 2001. – 380 с
Поиск по сайту: |
 ,
,  ,
, 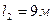 ,
,  ,
,  ,
,  ,
,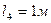 ,
, 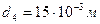 ,
,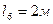 ,
,  ,
, 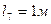 ,
,  ,
, 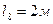 ,
, 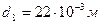 .
. ,
,  ,
,  ,
, 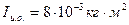 ,
, ,
, 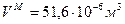 ,
, 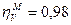 ,
, 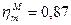 ,
, 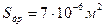

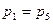 ;
; 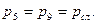
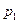 и
и 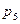 - давление в сечениях 1-1 и 5-5 напорного трубопровода, Па;
- давление в сечениях 1-1 и 5-5 напорного трубопровода, Па;  и
и  - давление в сечениях 6-6 и 9-9 сливного трубопровода, Па.
- давление в сечениях 6-6 и 9-9 сливного трубопровода, Па. ,
, - движущий момент,
- движущий момент,  ;
;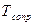 - момент сопротивления,
- момент сопротивления,  ;
;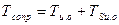 ,
, ;
; - рабочий объем гидромотора,
- рабочий объем гидромотора, 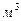 ;
; - перепад давления в гидромоторе, Па;
- перепад давления в гидромоторе, Па; 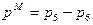 ;
;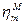 - механический КПД гидромотора;
- механический КПД гидромотора;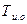 - момент сопротивления исполнительного органа,
- момент сопротивления исполнительного органа,  - момент трения исполнительного органа,
- момент трения исполнительного органа, 
 :
: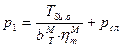 ,
,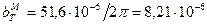 ,
, 
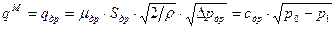 ,
, - расход гидромотора,
- расход гидромотора, 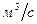 ;
; - расход дросселя,
- расход дросселя, 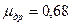 - коэффициент расхода дросселя;
- коэффициент расхода дросселя;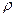 - плотность жидкость,
- плотность жидкость,  ;
;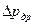 - перепад давления в дросселе, Па;
- перепад давления в дросселе, Па; 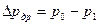 ;
;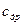 - коэффициент сопротивления дросселя,
- коэффициент сопротивления дросселя,  .
.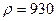

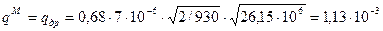
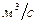
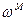 вала гидромотора:
вала гидромотора: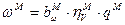 ,
,

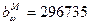
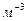 ;
; - объемный коэффициент полезного действия гидромотора.
- объемный коэффициент полезного действия гидромотора.
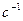 .
. ,
, 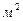
 ,
, 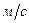

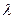

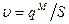
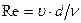 , где
, где 


 ,
, .
. ,
, 
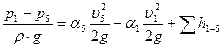 ;
;
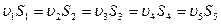 ;
;
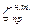 напорного трубопровода:
напорного трубопровода:
 .
.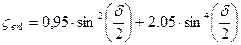

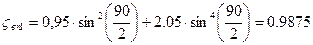 .
.
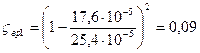 .
.



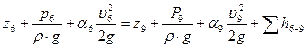 ;
; ,
,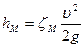 .
. ;
;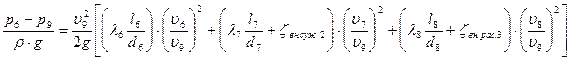 .
.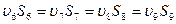 ;
;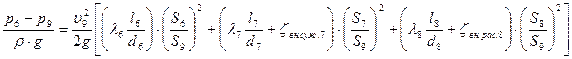 .
. сливного трубопровода:
сливного трубопровода: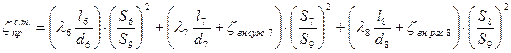 .
. , где
, где 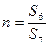 - степень сужения;
- степень сужения; .
.
 .
.

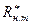 и сливного
и сливного  трубопроводов.
трубопроводов.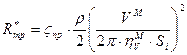 ,
,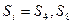 - площадь сечения, к которому осуществляется привидение.
- площадь сечения, к которому осуществляется привидение.


 - суммарный коэффициент сопротивления трубопроводов.
- суммарный коэффициент сопротивления трубопроводов.

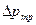 , определим
, определим 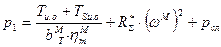
 (*)
(*)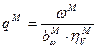 и выразим из полученного уравнения
и выразим из полученного уравнения 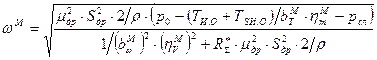

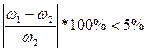
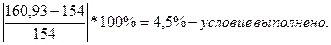
 , где
, где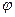 - угловое перемещение вала гидромотора, рад;
- угловое перемещение вала гидромотора, рад;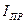 - приведенный момент инерции,
- приведенный момент инерции, 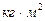 ;
;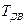 - движущий момент на валу гидромотора,
- движущий момент на валу гидромотора, 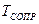 - момент сопротивления вала гидромотора,
- момент сопротивления вала гидромотора, 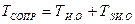 ;
;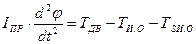
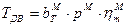 , где
, где
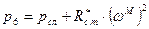
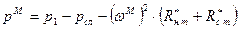
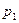 и подставим в уравнение выше:
и подставим в уравнение выше:

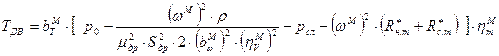

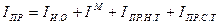 ;
;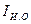 - момент инерции исполнительного органа,
- момент инерции исполнительного органа, 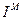 - момент инерции вала гидромотора,
- момент инерции вала гидромотора, 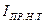 - приведенный момент инерции жидкости напорного трубопровода,
- приведенный момент инерции жидкости напорного трубопровода, 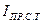 - приведенный момент инерции жидкости сливного трубопровода,
- приведенный момент инерции жидкости сливного трубопровода, 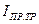 жидкости напорного и сливного трубопроводов, используя уравнение кинетической энергии жидкости.
жидкости напорного и сливного трубопроводов, используя уравнение кинетической энергии жидкости.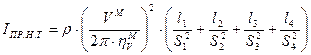 , где
, где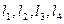 - длины участков напорного трубопровода,
- длины участков напорного трубопровода, 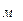 ;
; - площади участков напорного трубопровода,
- площади участков напорного трубопровода, 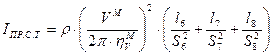
 - длины участков сливного трубопровода,
- длины участков сливного трубопровода,  - площади участков сливного трубопровода,
- площади участков сливного трубопровода, 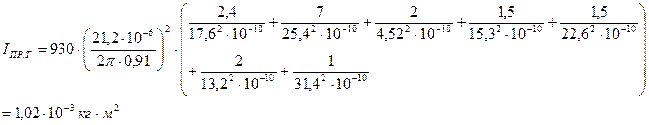
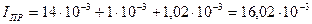
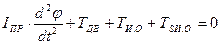
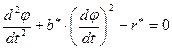

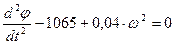 ,
,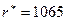
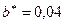
 - установившееся значение скорости вала гидромотора;
- установившееся значение скорости вала гидромотора; , где
, где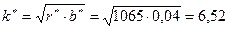




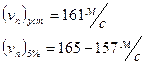
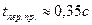
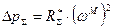

 - приведенный суммарный коэффициент сопротивления трубопровода;
- приведенный суммарный коэффициент сопротивления трубопровода;



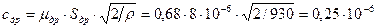
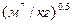

 , где
, где ,
, 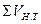 - суммарный объем напорного трубопровода,
- суммарный объем напорного трубопровода,  ;
; - приведенный модуль упругости системы «жидкость – напорный трубопровод», Па;
- приведенный модуль упругости системы «жидкость – напорный трубопровод», Па; , где
, где - средний радиус напорного трубопровода, м;
- средний радиус напорного трубопровода, м; - модуль упругости материала стенки трубопровода, Па;
- модуль упругости материала стенки трубопровода, Па;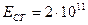 Па;
Па; - толщина стенки трубопровода, м;
- толщина стенки трубопровода, м;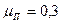 - коэффициент Пуассона;
- коэффициент Пуассона; - адиабатический модуль упругости жидкости, Па;
- адиабатический модуль упругости жидкости, Па; - адиабатическая скорость звука в жидкости,
- адиабатическая скорость звука в жидкости, 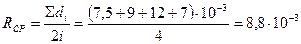
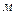 ;
;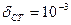
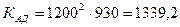 МПа;
МПа;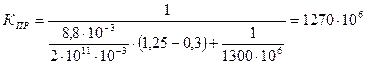 Па;
Па;
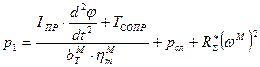
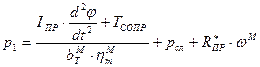
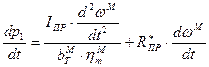


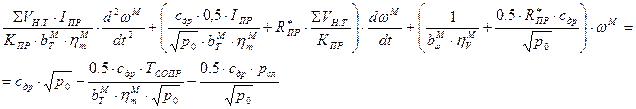
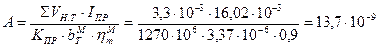

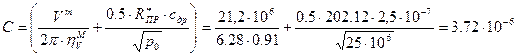

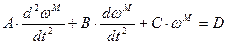
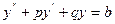 (*),
(*),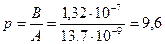
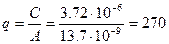

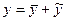 ,
, - общее решение дифф. уравнения второго порядка с правой частью;
- общее решение дифф. уравнения второго порядка с правой частью; - общее решение однородного уравнения (*);
- общее решение однородного уравнения (*); 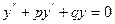 ;
; - частное решение неоднородного уравнения при
- частное решение неоднородного уравнения при 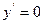 и
и 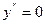 , определяемое зависимостью
, определяемое зависимостью  .
.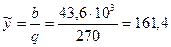
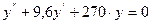
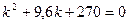
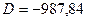
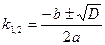
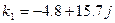
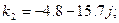 .
. и
и 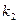 - сопряженные комплексные числа, поэтому
- сопряженные комплексные числа, поэтому 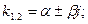
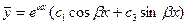
 и
и  . Для этого продифференцируем по времени величину
. Для этого продифференцируем по времени величину 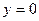 ,
, 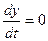 при
при  .
.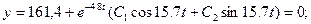
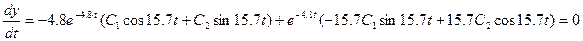
 :
: 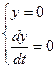 ;
;
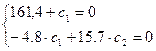
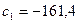 .
.