 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сравнение бесконечно больших функций
На первом уроке мы вычислили три предела с неопределённостью В перечисленных примерах используется стандартный приём деления числителя и знаменателя на «икс» в старшей степени и всё расписывается подробно. Но правильный ответ легко выяснить ещё до решения! В первом примере В таких случаях говорят, что функции числителя и знаменателя обладают одинаковым порядком роста. Или короче – числитель и знаменатель одного порядка роста. Действительно, в данном пределе и вверху, и внизу находятся квадратичные функции. Мир, равенство, братство. Во втором примере Здесь знаменатель более высокого порядка, чем числитель. Многочлен 4-ой степени растёт быстрее кубической функции и «перетягивает» предел на ноль. И, наконец, в пределе А в этом примере всё наоборот – числитель более высокого порядка, чем знаменатель. Квадратичная функция растёт быстрее линейной и «перетягивает» предел на «плюс бесконечность». Сделаем краткую теоретическую выжимку. Рассмотрим две произвольные функции 1) Если 2) Если 3) Если ! Примечание: при Подчеркиваю ещё раз, что данные факты относятся к произвольным функциям, определённым на бесконечности, а не только к многочленам. Но у нас ещё непаханое поле полиномов, поэтому, продолжаем работать с ними… да вы не грустите, для разнообразия я добавлю корней =) Пример 1 Найти предел В наличии неопределённость Старшая степень числителя равна двум. Знаменатель…. Как определить старшую степень, если многочлен под корнем? МЫСЛЕННО отбрасываем все слагаемые, кроме самого старшего: Почему бы сразу не узнать ответ? В числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые: Оформляем решение: Разделим числитель и знаменатель на
В действительности пару шагов можно пропустить, просто я подробно расписал, как в знаменателе под корень вносится Пример 2 Найти предел Это пример для самостоятельного решения. Постарайтесь провести рассуждения по образцу первого примера. Также заметьте, что здесь неопределённость Во избежание недочёта, всегда анализируйте, какая неопределённость получается в пределах рассматриваемого вида. Помимо неопределённости Пример 3 Найти предел Слишком трудный предел? Лёгкий испуг от хлопушки. Главное, грамотно управиться с радикалами. Проведём предварительный анализ: Сначала выясним старшую степень числителя. Там сумма двух корней. Под корнем Разбираемся с нижним этажом. Под корнем Сравниваем старшие степени: Оформляем решение, я распишу его максимально подробно: Разделим числитель и знаменатель на «икс» в старшей степени:
Ну и на всякий случай напоминаю формулу Другие члены знаменателя: Правила действий с корнями можно найти на странице Математические формулы и таблицы в методичке Горячие формулы школьного курса математики. Также на действиях с радикалами я подробно останавливался при нахождении производных. Пример 4 Найти предел Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость
Поиск по сайту: |
 :
:
 в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:
в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые: .
. аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:
аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:
 карлики тоже идут лесом:
карлики тоже идут лесом:
 , которые определены на бесконечности.
, которые определены на бесконечности. , где
, где  – ненулевая константа, то функции имеют одинаковый порядок роста. Если
– ненулевая константа, то функции имеют одинаковый порядок роста. Если  , то функции называют эквивалентными на бесконечности.
, то функции называют эквивалентными на бесконечности. , то функция
, то функция  более высокого порядка роста, чем
более высокого порядка роста, чем  .
. , то функция
, то функция  суть выкладок не меняется.
суть выкладок не меняется.
 и приём решения уже знаком – нужно разделить числитель и знаменатель на «икс» в старшей степени.
и приём решения уже знаком – нужно разделить числитель и знаменатель на «икс» в старшей степени. . Константу тоже отбрасываем и выясняем старшую степень знаменателя:
. Константу тоже отбрасываем и выясняем старшую степень знаменателя:  . Она тоже равна двум. Таким образом, числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу, отличному от нуля.
. Она тоже равна двум. Таким образом, числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу, отличному от нуля. . Таким образом, наши функции не только одного порядка роста, но ещё и эквивалентны на бесконечности.
. Таким образом, наши функции не только одного порядка роста, но ещё и эквивалентны на бесконечности.


 .
.
 , что необходимо отразить в решении. Примерный образец чистового оформления примера в конце урока.
, что необходимо отразить в решении. Примерный образец чистового оформления примера в конце урока. либо
либо  . Во всех четырёх случаях числитель и знаменатель необходимо разделить на «икс» в старшей степени.
. Во всех четырёх случаях числитель и знаменатель необходимо разделить на «икс» в старшей степени.
 отбросим младшее слагаемое:
отбросим младшее слагаемое:  и уберём константу:
и уберём константу:  . Под корнем
. Под корнем  отбросим все младшие слагаемые:
отбросим все младшие слагаемые: 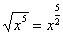 .
. , значит, старшая степень числителя:
, значит, старшая степень числителя:  .
. отбрасываем константу:
отбрасываем константу:  . У многочлена
. У многочлена  старшая степень равна двум.
старшая степень равна двум. , значит, старшая степень знаменателя:
, значит, старшая степень знаменателя:  .
.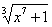 более высокого порядка роста, чем
более высокого порядка роста, чем  , следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности.
, следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности.
 :
:
 «разнокалиберные» корни, и квадратный корень
«разнокалиберные» корни, и квадратный корень  необходимо «подогнать» под кубический корень
необходимо «подогнать» под кубический корень  . Составим и решим уравнение:
. Составим и решим уравнение:  . Таким образом:
. Таким образом:  .
.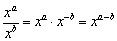 , по которой выполняется деление:
, по которой выполняется деление:


 более высокого порядка роста, чем корень
более высокого порядка роста, чем корень  ).
).