 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Непрерывность и разрывы функции
КРАТКИЙ КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ «Элементы высшей математики» Лекция 6. Пределы Вопросы для изучения: 1. Общее понятие предела переменной величины. 2. Предел функции. 3. Теоремы о пределах. 4. Замечательные пределы. 5. Вычисление пределов. 6. Непрерывность и разрывы функции.
Общее понятие предела переменной величины Рассмотрим некоторую последовательность, зависящую от натурального аргумента xn=f(n) (n
Легко заметить, что при возрастании n члены последовательности все ближе подходят к значению А=2. Если вокруг этого значения выделить какую-то область радиусом e (e-окрестность), то при некотором n xn войдет в эту окрестность и уже не выйдет из нее, какой бы малой она ни была. Это и означает, что А - предел, к которому стремится последовательность хn.
Так что, если в некотором процессе изменение xn таково, что в какой-то момент он попадает в e-окрестность числа А и не выходит из нее, то А - предел величины xn:
Рассмотрим последовательность xn = n, n
Здесь другой случай: если задаться любым числом М, то всегданайдется такое число n, что xn+1 будет больше М. Эта последовательность не имеет предела. Условно записывают:
и называют xn бесконечно большой Для последовательности хn=
Последнее, что отметим: переменная, зависящая от натурального аргумента, может иметь только один предел.
Предел функции Пусть теперь для некоторой функции у=f(х) процесс таков, что х стремится к числу а. Выясним, к чему стремится функция у. Если двигаться от 0 к точке х=а, то в некоторый момент войдем в e-окрестность числа а. При этом функция (при движении по графику) будет ограничена по оси оY d-окрестностью, увязанной с e-окрестностью по оси оХ, и неизбежно приходит в точку х=а, принимая значение А.
Таким образом, изменение функции у=f(х), в конечном итоге, приводит к тому, что ее значения не выйдут за пределы e-d окрестности точки, которая и является ее пределом:
Функция может и не иметь предела. Тогда
Бесконечно малые (б.м.) и бесконечно большие (б.б.) величины Так как б.м. и б.б. часто встречаются в анализе, то сформулируем их свойства. Для удобства положим a(х) - б.м., b(х) - б.б. величины при х
1. Если функция у=f(х) может быть представлена суммой постоянного числа А и б.м. величины a(х), т.е. у=А+a, то lim y = A и обратно, если lim y = A, то у=А+a. 2. Сумма нескольких б.м. величин тоже является б.м. величиной. 3. Произведение б.м. величины на ограниченную функцию (или число) также является б.м. величиной. 4. Частное от деления б.м. величины на ненулевую ограниченную функцию (или число) является б.м. величиной. 5. Произведение б.б. величины на ограниченную функцию (или число) также является б.б. величиной. 6. Сумма б.б. величины и ограниченной функции (или числа) является б.б. величиной. 7. Частное от деления б.б. величины на ненулевую ограниченную функцию (или число) является б.б. величиной 8. Величина, обратная б.м. величине, является б.б. величиной: b(х)=
Теоремы о пределах Для того, чтобы вычислять пределы, разработан ряд удобных теорем, которые приведем без доказательств:
· Пределпостоянной величины (числа) равен этой постоянной: lim C=C. · Пределсуммы равен сумме пределов: lim(u+v-w)=lim u+ lim v- lim w. · Пределпроизведения равен произведению пределов: o o lim(u · Предел дроби равен частному пределов числителя и знаменателя при условии, что знаменатель - не б.м. величина: lim · В неравенствах можно переходить к пределу, т.е., если u<v (или другой знак неравенства), то lim u<lim v
Замечательные пределы Ряд достаточно часто встречающихся в практике пределов по историческим причинам получил название замечательных. Приведем некоторые из них, встречающиеся в практических задачах: · ·
· · ·
Вычисление пределов
1. Прямая подстановка: 2. Упрощение функций. Если при прямой подстановке получается неопределенное выражение типов:
В последнем примере учтено, что, если х
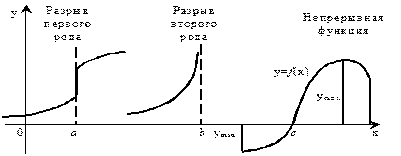
Непрерывность и разрывы функции Функция f(x) называется непрерывной в точке x0 если она:
· Определена в этой точке, т.е. существует f(x0). · Имеет предел в этой точке · Пределсовпадает со значением функции А=f(x0).
Если хотя бы одно из этих условий нарушено, то функция разрывная в точке x0. Этот разрыв может быть конечен - скачок (разрыв первого рода), или бесконечен (второго рода).
Для функций, непрерывных в точке x0 сумма f1+f2, произведение f1
Если функция y= f1(u) непрерывна в точке u0, а функция u= f2(x) непрерывна в точке f2(x0), то, при u0= f2(x0), сложная функция f1(f2(x)) тоже непрерывна в этой точке, т.е. можно записать:
Функция y= f(x) называется непрерывной на интервале a
· Она ограничена на этом интервале сверху и снизу (не может быть бесконечного значения). · Обязательно имеет минимальное и максимальное значения. · Если по концам интервала функция имеет разные знаки, то внутри интервала имеется хотя бы одна точка х=с, в которой f(с)=0 (корень функции).
Примеры решения задач
Понятие предела позволяет прогнозировать поведение различных процессов или моделей как на бесконечности, так и в конкретных точках. На ряде примеров покажем основные методы вычисления пределов. 1.
В любой задаче на пределы сначала рассматривается прямая подстановка Ответ: 13. 2.. Решение: Ответ: функция бесконечно малая при 3. Решение: Ответ: 1. 4.. Решение:
Здесь использована теорема: величина, обратная бесконечно большой, является бесконечно малой, т.е. 0. 5. Решение: В данном случае прямая подстановка привела к неопределенности. Попробуем упростить функцию: Таким образом, Ответ: функция – бесконечно малая при х 6. Решение: Используем разложение квадратного трехчлена на множители по известной формуле: Тогда. Следовательно,. Ответ: 0,5625. 7. Решение:
В этом случае следует разделить числитель и знаменатель на старшую степень аргумента, т.е. на х3, и использовать теорему . Ответ: 8.. Решение: Ответ: функция – бесконечно большая при 9. Вспомним первый замечательный предел Для приведения заданного выражения к такому виду введем замену переменной: u=3x; отсюда Следовательно, Для аргумента: Таким образом, Ответ: 3. 10.. Используем второй замечательный предел в форме: Заменяем переменную: Ответ: е2. 11. Используем второй замечательный предел в форме: Заменяем переменную: Таким образом: Ответ: Вопросы для самоконтроля: 1. Определение предела переменной величины. 2. Определение предела функции. 3. Бесконечно малые (б.м.) и бесконечно большие (б.б.) величины. 4. Свойства б.м. и б.б. величин. 5. Теоремы о пределах. 6. Замечательные пределы. 7. Методы вычисления пределов. 8. Непрерывность функции в точке и на интервале. 9. Свойства функций, непрерывных в точке. 10. Непрерывность сложной функции. 11. Типы разрывов функции. 12. Свойства функций, непрерывных на интервале.
Тренировочные задачи Вычислить пределы: · Ответ: 4,5 · Ответ: 0
· Ответ: · Ответ: 1,25
· Ответ: 0,125 · Ответ: 0,6
Поиск по сайту: |
N), например: хn=2+(-1)n 
, т.е.{1; 2,50; 1,67; 2,25; 1,80,...}:
.
N, т. е. {1; 2; 3;... }.
; 
;...} при возрастании номера n пределом является А=0, т.е. 
. Если предел равен 0, то величина называется бесконечно малой.
.
. Но где-нибудь рядом предел может быть: 
. Если 
, то функция называется бесконечно большой в точке х=а (вариант 
). Если 
, то функция называется бесконечно малой в точке х=а (вариант 
).
а (или х 
).
; Величина, обратная б.б. величине, является б.м. величиной: a(х)= 
.
.
, где е=2,718281828...
. Это - наиболее общий прием, который всегда используется первым: 
.
, 
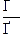и некоторых других, то выделение общего множителя или приведение к замечательным пределам приводят к нужному результату:
0, то, очевидно, и 5х 
(при f2¹0) также непрерывны в этой точке.
x 
.
. Если при этом получается конечное значение (в том числе и 0) или , или – то расчет закончен. В данном примере 
.
.
.
.
.
.
.
, где 
.
, т.е.
.
.
.
.
, т.е. 
или 
.
.
.
, откуда 
и 
. Из 
следует 
и 
. Таким образом: 
.
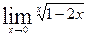
, откуда 
. Из 
и 
.
.
.
.
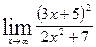