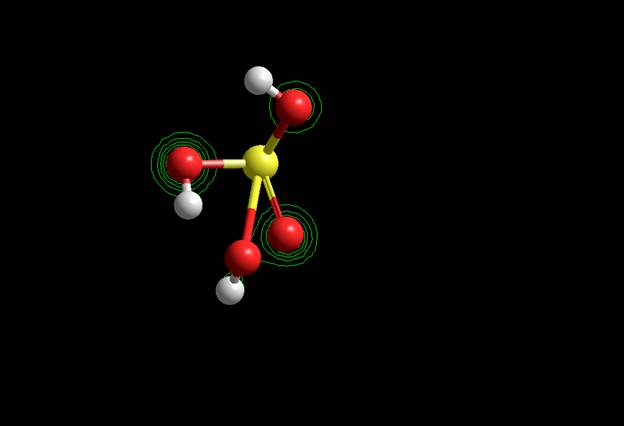
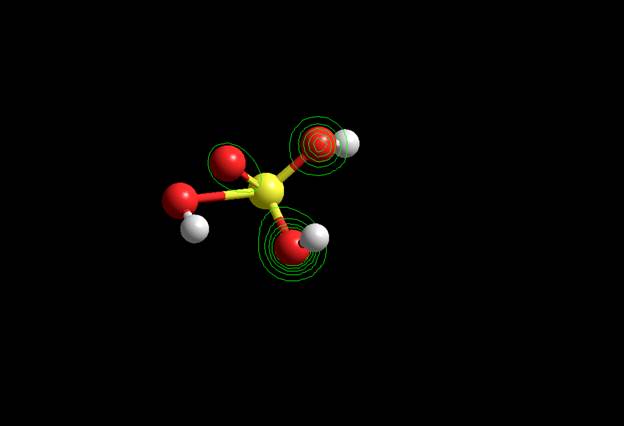
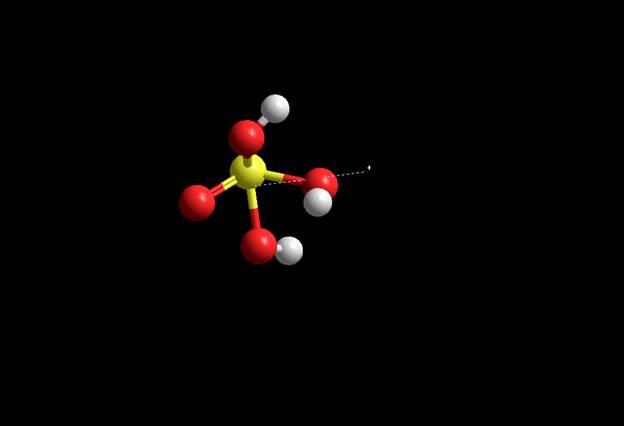
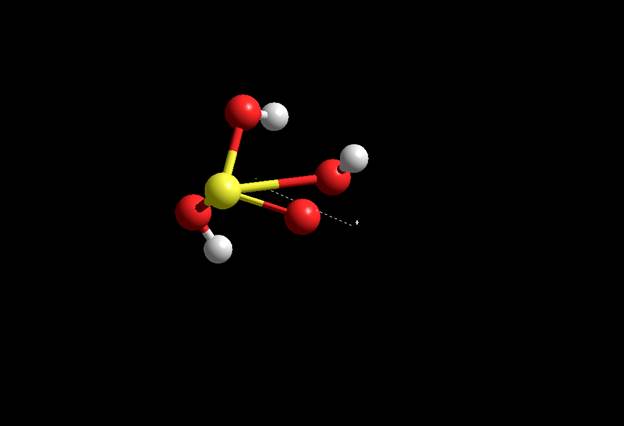
Волновые функции LUMO HOMO (Semi-empirical)

Задание

1. Создание молекулы состоящей из 8 атомов

2. Исследовать свойства, получение и применение молекулы

3. Оптимизировать геометрию молекулы в прграмме HyperChem

4. Рассчитать, используя 4 метода (ММ, ab-inito, полуэмпирические - 2 метода):

· Геометрию частицы: расстояния, углы, координаты

· Потенциальную энергию и её градиент

· Распределение электростатического потенциала

· Дипольный, квадрупольный момент и тензор поляризации

· Момент инерции и частоты вращения

· Колебательный спектр частицы и выделить 3 фазы

· Электронный спектр частицы

· Спектр энергетических уровней и их заселённости

· Волновые функции LUMO HOMO

· Электронные спектры для 3 фаз колебаний частицы

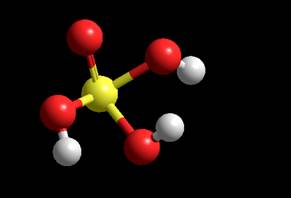
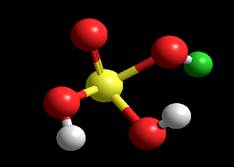
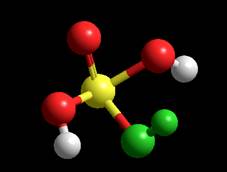
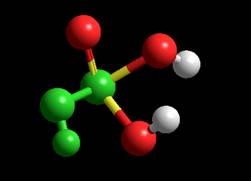
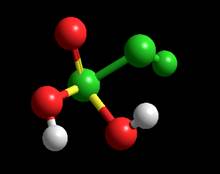
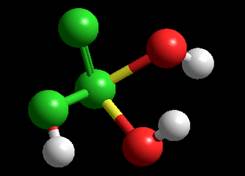
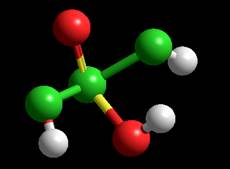
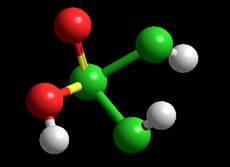
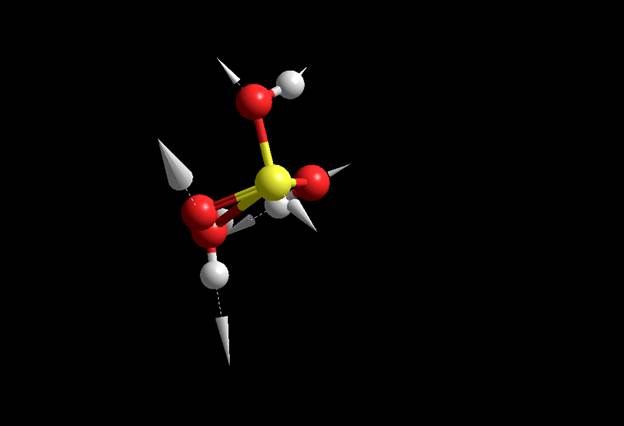
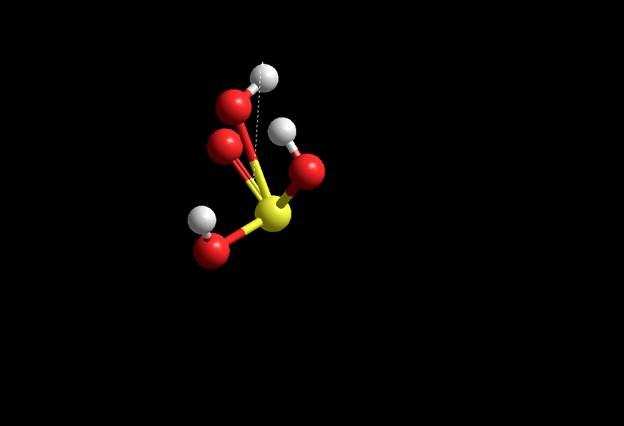
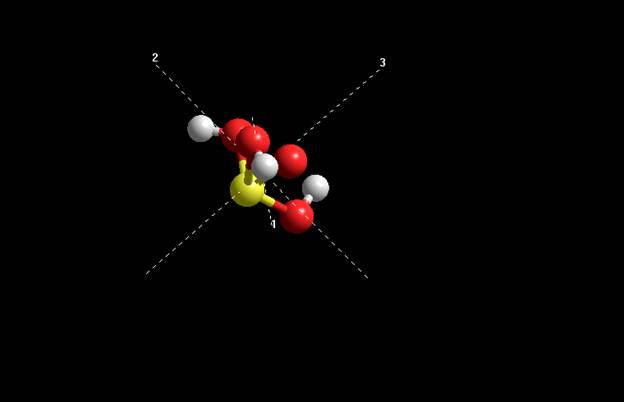
Геометрия частицы

MM+

Координаты:

-6.86855 -3.5811 7.63634 -7.189 -2.58248 6.38402

-5.47909 -2.67013 6.72762 -8.15077 -2.14698 7.77163

-6.75676 -0.917878 6.65705 -5.11093 -1.85051 6.45577

-6.98811 -0.715059 7.54389 -8.82773 -1.59323 7.4235

Расстояния:

P-O

1.63348A 1.74629A

1.7436A 1.74134A

O-H

0.938732A 0.938691A

0.941332A

Углы:Угол между P, O и H –

107.068 106.452

104.436 1

Угол между P, O и O –

114.551 68.061

69.5599 113.332

76.9429 76.9014

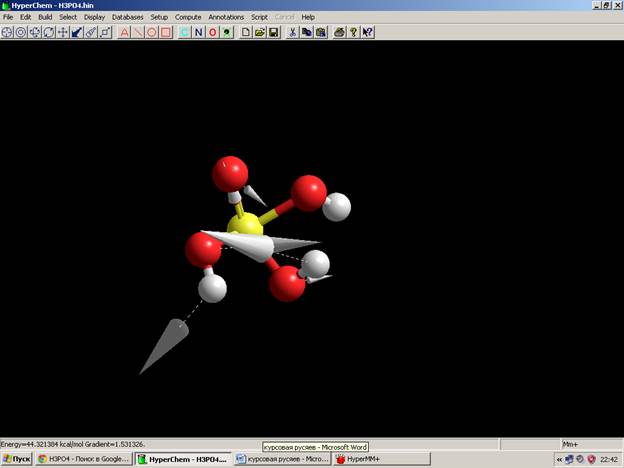
Расчет потенциальной энергии и её градиента

MM+

Выбрав в меню Compute команду Single point, получим энергию и градиент энергии , которая отобразится в строке состояния:

Energy = 44,321384 kcal/mol

Gradient = 1,531326

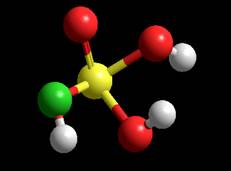
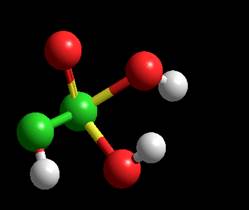
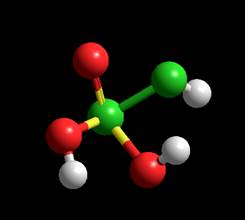
Semi-empirical

CNDO

Energy = -929.9258kcal/mol

Gradient = 8.816

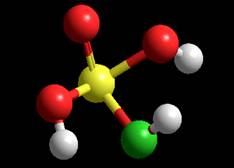
INDO

Energy = -758.243076 kcal/mol

Gradient = 23.115724

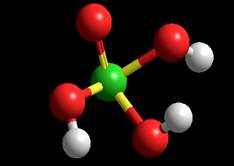
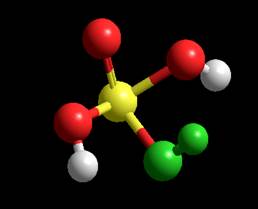
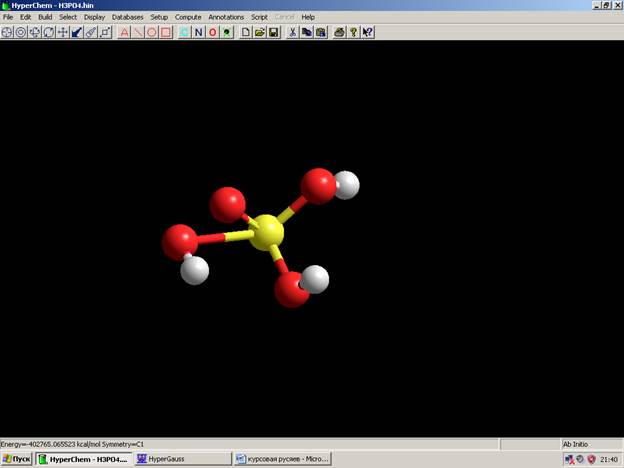
Ab Inito

Energy = -402765.065523 kcal/mol

Распределение электрического заряда колеблющейся структуры (MM+)

1. Для получения контурного графика распределения электронной плотности открываем ячейку диалога Plot Molecular graphs в меню Compute.

2. Выбираем Total Charge Density и 2D Contour в этой диалоговой ячейке.

3. Щелкаем на таблице Contour Grid, и затем устанавливаем горизонтальные и вертикальные точки сетки на 64 и контурные уровни на 10.

Распределение электрического заряда колеблющейся структуры (Semi-empirical) СNDO

INDO

Ab Inito

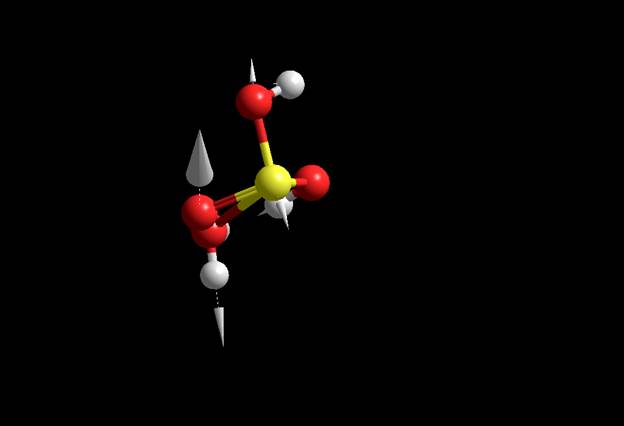
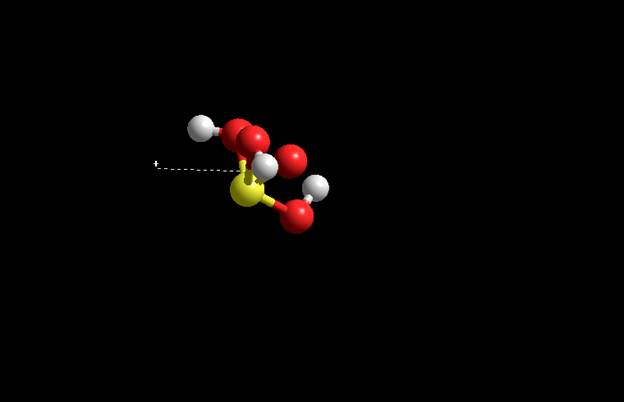
Дипольный, квадрупольный момент и тензор поляризации

Дипольный момент

MM+

1. Compute далее Molecular Dinamics

2. Display далее Show Dipole Moment

Dipole Moment 1.54886 (1.33268, -0.718222, 0.327255)

Semi-empirical

CNDO

Dipole Moment 2.841 (1.97415, -0.0712122, -2.04181)

INDO

Dipole Moment 3.73702 (-0.540859, -3,39628, -1,46221)

Ab Inito

Dipole Moment 1.57845 (0.93645, -1.09875, -0.638215)

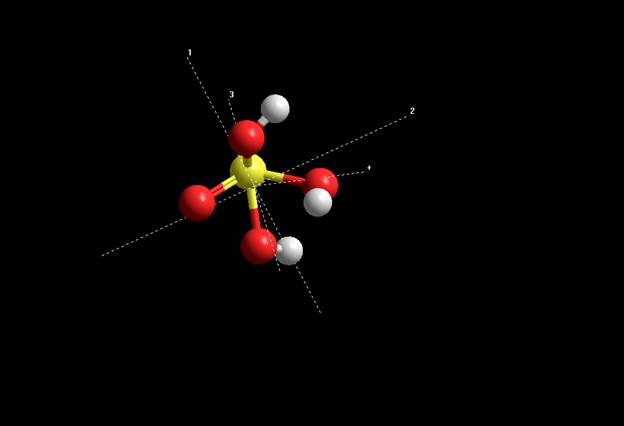
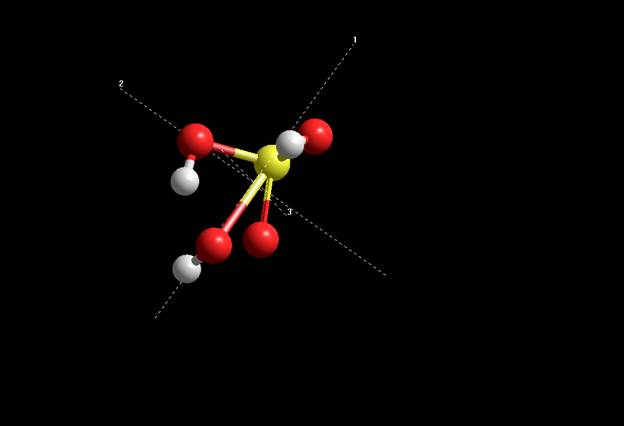
Момент инерции и частоты вращения

Момент инерции

Display далее Show Inertial Axes

Moments of inertia: 85.4515, 96.9733, 147.179

Semi-empirical

CNDO

Moments of inertia: 96.8538, 159.409, 192.181

INDO

Moments of inertia: 98.3218, 158.935, 193.604

Ab Inito

Moments of inertia: 68.9677, 147.719, 185.863

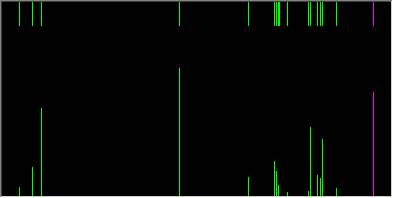
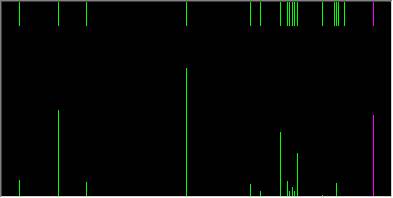
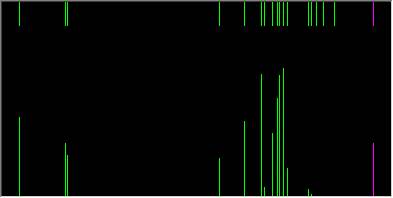
Колебательный спектр частицы

1. Compute далее Vibration, Rotation Analysis

2. Compute далее Vibrational Spectrum

Semi-empirical

CNDO

INDO

Ab Inito

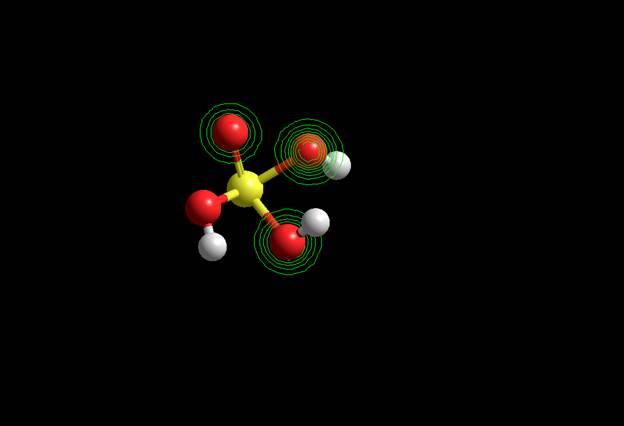
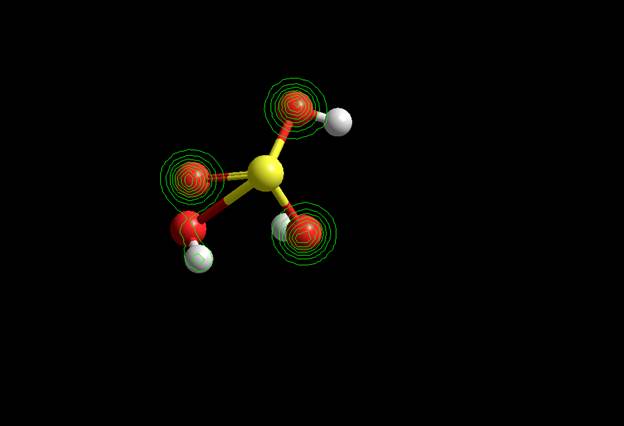
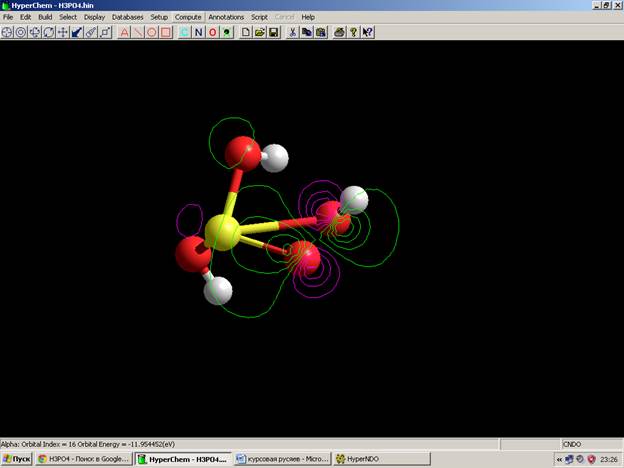
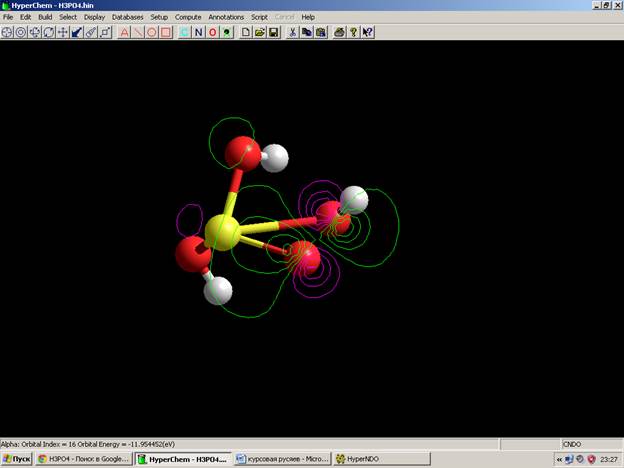
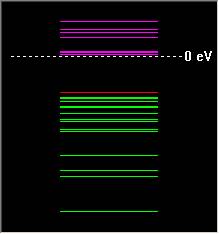
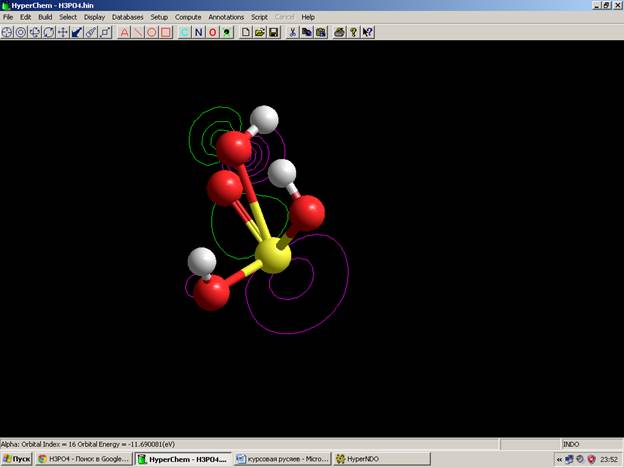
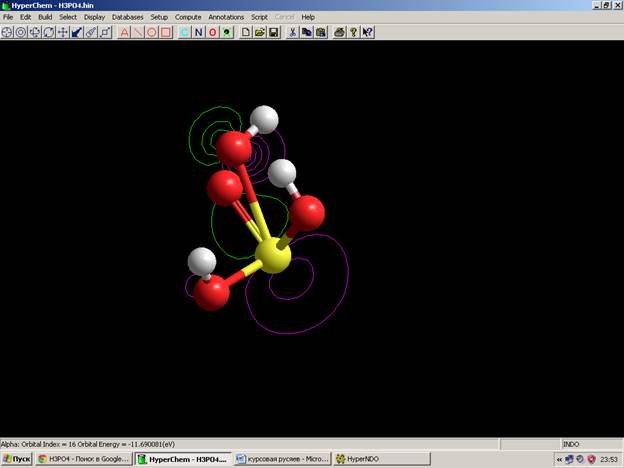
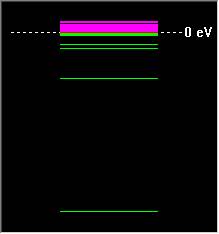
Электронный спектр частицы

Спектр энергетических уровней и их заселённости

Волновые функции LUMO HOMO (Semi-empirical)

CNDO

HOMO

LUMO

INDO

HOMO

LUMO

Ab Inito

HOMO

LUMO

Поиск по сайту: