 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Замечательные пределы
Предел числовой последовательности. Число a называется пределом числовой последовательности ( Пишут: Последовательность, имеющая предел называется сходящейся. Последовательность, не имеющая предела, называется расходящейся. Последовательность, предел которой равен нулю, называется бесконечно малой последовательностью. Последовательность, не имеющая предела, называется бесконечно большой. Теоремы о пределах: 1). Предел суммы (разности) двух последовательностей равен сумме(разности) пределов этих последовательностей, т.е. 2). Предел произведения двух последовательностей равен произведению пределов этих последовательностей, т.е. Следствие: Постоянный множитель можно выносить за знак предела. 3). Предел частного двух последовательностей равен частному пределов этих последовательностей, т.е. 4).Предел числа равен самому числу. Пример: 1). 2). 3). 4). 5). Самостоятельно: 1). 5).
Число b называется пределом функции f(x), если при х⟶a сама функция стремится к числу b. Свойства и теоремы, применяемые для нахождения пределов последовательностей, справедливы и для нахождения пределов функций. Пример: 1). 2). 3). 4). 5). D= 4
= 6). 7). 8). = 9). = Замечательные пределы. Первым замечательным пределом называется Пример: 1) 2) 3) = 1 Самостоятельно: Н.В.Богомолов, стр.171, № 251(1,3), 253(4). Числом е ( вторым замечательным пределом) называется предел числовой последовательности е = Пример:1) 2) 3) Самостоятельно: Н.В.Богомолов, стр.82, № 33(1,2), 34(1), 35(2). Дома:стр.82, № 36,37,38(1),40,41. Стр.171, № 251(3,4), 253(3).
Домашняя работа: №36. 1)
= 2) D = 4
=
№37. 1) = = 2) = №38(1). 1)
= №40.
= 2) = = №41.
Односторонние пределы. В приведенном определении предела функции 𝔁⟶а (т.е. 𝔁 может быть как меньше Если при нахождении предела функции рассматривать значения 𝔁 только слева от Если при нахождении предела функции рассматривать значения 𝔁 только справа от Левый и правый пределы называют односторонними пределами. Пример: 1 1,1 Непрерывность функции. Функция f(𝔁) называется непрерывной в точке 2). f(𝔁) имеет конечный предел при 𝔁⟶ 3). Этот предел равен значению функции в точке
Пример: Исследовать непрерывность в точке 𝔁 = 0 следующих функций: 1). y = D(y) = 𝔁 В точке 𝔁 = 0 функция не является непрерывной, т.к. нарушено первое условие непрерывности .
y
0 𝔁
2). y = 𝔁 + 1, при 𝔁 𝔁 1). 𝔁 = 0 2).
y •1
0 𝔁
°
3). y = 1, при 𝔁 = 0. 1). 𝔁 = 0 2).
⟹ 3). f(0) Нарушено третье условие непрерывности, ⟹ функция в точке 𝔁 = 0 не является непрерывной. y •1 ° 𝔁
4). y = 1).D(y) = 𝔁 2).
3). f(0) = Выполнились все три условия непрерывности функции, ⟹ в точке 𝔁 =0 функция является непрерывной. y
0 𝔁 Если условие непрерывности в точке 𝔁 = Для элементарных функций справедливы следующие положения: 1.). область непрерывности элементарных функций совпадает с ее областью определения., 2). Элементарная функция может иметь разрыв только в отдельных точках какого – либо промежутка; 3). Элементарная функция может иметь разрыв только в той точке, в которой она неопределена. Если функция y = f(𝔁) при 𝔁 = а имеет разрыв, то для выяснения характера разрыва следует найти левый и правый пределы: 1). Если 2). Если хотя бы один из односторонних пределов не существует или равен Примеры: 1). y = D(f) = 𝔁
Асимптоты. Асимптотой кривой называется прямая, к которой неограниченно приближается точка графика при неограниченном удалении ее от начала координат. Различают вертикальные, горизонтальные, наклонные асимптоты. Вертикальные асимптоты: График функции
Поиск по сайту: |
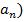 , если при n⟶
, если при n⟶  сама последовательность стремится к числу a.
сама последовательность стремится к числу a. = a.
= a. =
=  ;
; =
=  ;
; =
=  ;
; =
=  =
= 
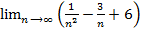 =
=  = 0
= 0  = 6,
= 6, =
=  =
=  (т.к. первая бесконечность растет быстрее, чем вторая).
(т.к. первая бесконечность растет быстрее, чем вторая).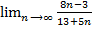 =(
=(  = получили неопределенность вида
= получили неопределенность вида  , чтобы ее раскрыть надо каждый член последовательности разделить на старшую степень =
, чтобы ее раскрыть надо каждый член последовательности разделить на старшую степень =  =
=  =
= 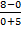 =
=  = 1,6.
= 1,6.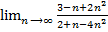 = (
= (  =
=  =
=  =
=  =
= 
 ,
, ; 2)
; 2)  ; 3).
; 3).  ; 4).
; 4). 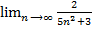 ;
; ; 6)
; 6)  ; 7)
; 7)  .
.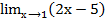 = 2
= 2  =
= 
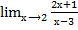 =
=  =
=  ;
; =
=  = получили неопределенность
= получили неопределенность  , чтобы ее раскрыть надо числитель и знаменатель дроби разложить на множители и выполнить сокращение. =
, чтобы ее раскрыть надо числитель и знаменатель дроби разложить на множители и выполнить сокращение. =  =
= 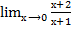 = 2,
= 2,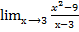 = (
= ( 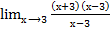 =
=  = 3+ 3 = 6,
= 3+ 3 = 6, =
=  = 0 2
= 0 2  =
= D = 1
D = 1  8 = 9,
8 = 9, =
=  =
= 
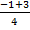 =
=  ,
, =
=  =
= 
 =
=  =
=  =
= 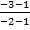 =
=  ;
; =
=  =
=  =
= 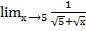 =
=  ;
; =
=  =
=  =
=  =
=  =
= 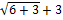 = 3
= 3 
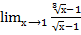 =
=  =
=  =
=  =
= =
=  =
=  ;
; =
=  = получили неопределенность вида
= получили неопределенность вида 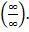 =
=  =
= 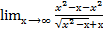 =
= =
=  =
= 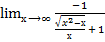 =
=  =
= 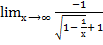 =
=  =
=  .
. = 1, или
= 1, или  = 1.
= 1. = (
= ( 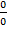 ) =
) =  =
=  =
=  =1,5.
=1,5. =
=  =
=  =
= 
 =
= 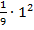 =
=  = (
= ( 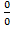 ) =
) = 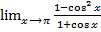 =
=  =
= 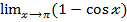 =
= = 2.
= 2. , или е =
, или е =  . Неопред.
. Неопред. 
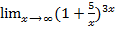 =
=  =
=  =
=  .
. =
= 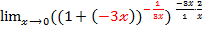 =
=  =
=  .
. =
=  =
=  =
=  =
=  .
. =0,
=0, 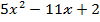 = 0
= 0 =
=  =(
=( 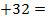 81, D = 121
81, D = 121  81,
81,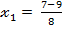 =
=  ;
;  =
=  ;
;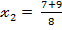 = 2.
= 2.  = 2.
= 2.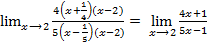 =
=  =
=  =1.
=1. = (
= (  =0 =
=0 =  =
= 64.
64. =
= 
 = 3.
= 3. =
=  =
=  = 1
= 1  .
. ;
; = (
= (  =
=  =
= =
=  =
=  =
= 
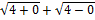 = 2
= 2 
 =
= 
 =
=  =
=  =
=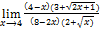 =
=  =
=  =
=  =
=  =
=  .
.
 =(
=( 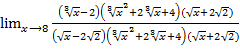 =
= 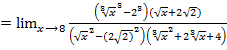 =
= 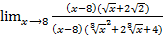 =
=  =
=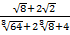 =
=  =
=  =
=  .
. = (
= (  ) =
) =  =
=  =
= 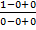 =
= =
= 
 = (
= (  =
=  =
= =
=  =
= 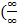 ) =
) =  =
= =
= 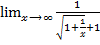 =
= 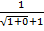 =
= 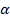 , так и больше
, так и больше  .
. .
. =
=  =
=  =
= 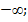 0,9
0,9 =
=  =
=  • 𝔁
• 𝔁 если она удовлетворяет следующим трем условиям: 1). f(𝔁) определена в точке
если она удовлетворяет следующим трем условиям: 1). f(𝔁) определена в точке  ,
,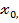
 = f(
= f(  ;
;


 ,т.е. функция в точке 0 определена, f(0) = 1.
,т.е. функция в точке 0 определена, f(0) = 1. =
=  =
=  =
=  =
= 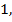
 , ⟹ в точке 𝔁 = 0 функция не является непрерывной, т.к. нарушено второе условие непрерывности.
, ⟹ в точке 𝔁 = 0 функция не является непрерывной, т.к. нарушено второе условие непрерывности.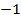
 , при 𝔁
, при 𝔁 
 ,т.е. функция в точке 𝔁 = 0 определена, f(0) =1,
,т.е. функция в точке 𝔁 = 0 определена, f(0) =1, =
= 
 =
=  =
=  = 0,
= 0, ,
, , f(0) = 0
, f(0) = 0 =
=  =
=  .
. нарушено . то такую точку называют точкой разрыва функции.
нарушено . то такую точку называют точкой разрыва функции. конечные, то 𝔁 = а – точка разрыва I рода,
конечные, то 𝔁 = а – точка разрыва I рода, , то 𝔁 = а – точка разрыва II рода.
, то 𝔁 = а – точка разрыва II рода.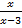 ;
; , ⟹ 𝔁 =3 – точка разрыва.
, ⟹ 𝔁 =3 – точка разрыва. =
=  =
= 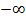 , ⟹ 𝔁 =3 – точка разрыва II рода.
, ⟹ 𝔁 =3 – точка разрыва II рода.