|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связь между бесконечно большими и бесконечно малыми функциями ⇐ ПредыдущаяСтр 3 из 3
Теорема. 1.)Пусть функция 2.)Пусть
Доказательство. (1).
Для функции (2).
Для функции Пример:
Предельный переход в неравенстве. Теорема. Пусть
Доказательство. Предположим, что
Пусть
Получили противоречие: Наше предположение неверно, значит Примеры: 1.)
2.)
Единственность предела. Теорема. Если
Доказательство. Предполагаем, что есть 2 предела (
Пусть
Пусть
Получили противоречие: По теореме о предельном переходе в неравенстве:
Односторонние пределы. Односторонние пределы – это предел “слева” и предел “справа”. 1.)Предел “слева”;
2.)Предел “справа”.
Функция
Пример: 1.)
Теорема о промежуточной переменной. Пусть Пусть Доказательство.
1
Найдём предел
По теореме о промежуточной переменной: а.)
б.)
Неопределённости.
Примеры на раскрытие неопределённостей:
2 1.) 2.) 3.) Пример:
Вычисление
Если функция непрерывна, то
Основное логарифмическое тождество:
Примеры:
Пределы, получаемые с помощью 2
Пример:
2.) Частный случай: Пример:
3.) Пример:
Поиск по сайту: |
 – бесконечно малая при
– бесконечно малая при 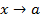 и
и  в достаточно малой окрестности точки
в достаточно малой окрестности точки  , тогда
, тогда  бесконечно большая при
бесконечно большая при  – бесконечно большая при
– бесконечно большая при  бесконечно малая при
бесконечно малая при 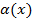 – бесконечно малая при
– бесконечно малая при  выполняется неравенство
выполняется неравенство ;
;
 ;
; ;
;
 выполняется неравенство
выполняется неравенство  >
> 
 выполняется определение бесконечно большой функции (по любому
выполняется определение бесконечно большой функции (по любому 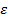 находится
находится 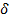 ) при
) при  выполняется неравенство
выполняется неравенство 



 выполняется неравенство
выполняется неравенство 
 выполняется определение бесконечно малой функции (по любому
выполняется определение бесконечно малой функции (по любому 

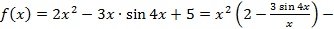 бесконечно большая при
бесконечно большая при 
 выполняется неравенство
выполняется неравенство  , при этом каждая из функций имеет конечный предел:
, при этом каждая из функций имеет конечный предел: ,
,  , тогда
, тогда  .
.

 выполняется неравенство
выполняется неравенство 
 ;
;
 ;
;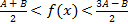
 выполняется неравенство
выполняется неравенство 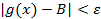 ;
; ;
; ;
; ;
;
 выполняется неравенство
выполняется неравенство 
 ;
; , а по условию
, а по условию  ,
,  +1,
+1,  ;
;


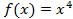 ,
,  ,
, 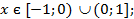



 ;
;

 в точке
в точке  имеет конечный предел
имеет конечный предел  , то данный предел является единственным.
, то данный предел является единственным.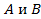 );
);


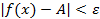 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; выполняется неравенство
выполняется неравенство 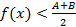
 , а по условию
, а по условию 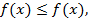 значит
значит  ;
; ;
;
 ;
;





 имеет конечный предел
имеет конечный предел  , при
, при 





 выполняется неравенство
выполняется неравенство 
 , тогда
, тогда  .
. выполняется неравенство
выполняется неравенство
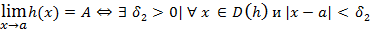 выполняется неравенство
выполняется неравенство

 выполняется неравенство
выполняется неравенство 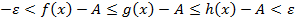
 , определение предела выполнено(
, определение предела выполнено(  выполняется неравенство
выполняется неравенство  ) .
) . замечательный предел.
замечательный предел.

 ;
; ;
; ;
; ;
; ;
; <
<  x<
x<  ; | ∙
; | ∙ 
 ;
;
 :
:
 ;
; 











 ;
;












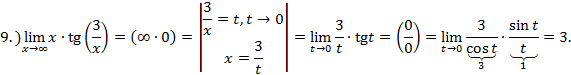
 замечательный предел.
замечательный предел. где
где 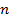 – натуральное число (Л.Эйлер(1707-1783));
– натуральное число (Л.Эйлер(1707-1783)); ;
;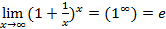 .
.
 замечательного предела.
замечательного предела.


 ;
;
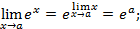
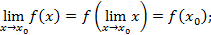




 бесконечно малая функция.
бесконечно малая функция.


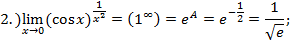
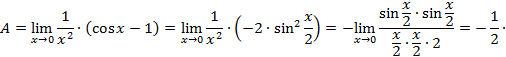
 замечательного предела.
замечательного предела.