 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сравнение бесконечно малых и бесконечно больших функций
Лекция 19
19.1.Предел функции на бесконечности Определение 19.1. Число А называется пределом функции f(x) при Определение 19.2. Число А называется пределом функции f(x) при если для любой бесконечно большой последовательности значений аргумента, элементы
Некоторые свойства функций, имеющих предел Теорема 19.1 (об ограниченности функций, имеющих предел) Если Доказательство
Пусть
Теорема 19.2. Если
Теорема 19.3. Если
Теорема19.4(арифметические операции над функциями, имеющими предел). Если существуют
Доказательство Для любой последовательности По определению 18.1 Остальные формулы доказываются аналогично.
Следствие. Если существует Теорема 19.5. Пусть Пусть для любого
Два замечательных предела Докажем, что Рассмотрим дугу окружности OA=R=1 c центральным углом Тогда MK=sin x, AN=tg x.
Так как функции
Так как
Пример 19.1 Вычислить
Заметим
Бесконечно малые и бесконечно большие функции Определение 19.3 Свойства бесконечно малых функций
Определение 19.4
Замечание 1. Бесконечно большая функция не имеет предела при Пример 19.2.
Замечание 2. Выражения вида
Сравнение бесконечно малых и бесконечно больших функций Рассмотрим функции
Определение 19.5. Если Определение 19.6. Если
Определение 19.7 Если f(x) и g(x) – бесконечно малые (бесконечно большие) функции при ( Замечание 3. В случае бесконечно малых функций часто используют символ «о»:
В примере 19.1. Теорема 19.6. (замена функций эквивалентными при вычислении пределов) Пусть Доказательство 1). Пусть существует
2)
Пример 19.3. Вычислить
Поиск по сайту: |
 , если для любой бесконечно большой последовательности
, если для любой бесконечно большой последовательности 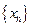 соответствующая последовательность
соответствующая последовательность  сходится к А.
сходится к А. .
.
 которой положительны (отрицательны), соответствующая последовательность значений функции сходится к А.
которой положительны (отрицательны), соответствующая последовательность значений функции сходится к А. , то существует некоторая проколотая окрестность этой точки
, то существует некоторая проколотая окрестность этой точки  , в которой функция ограничена.
, в которой функция ограничена.

 .
. , то
, то  .
. в некоторой окрестности точки
в некоторой окрестности точки  .
. то существуют конечные пределы
то существуют конечные пределы 

 , если
, если  , причем
, причем 
 ,
, 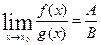 (19.1).
(19.1). формулы (19.1) справедливы, следовательно:
формулы (19.1) справедливы, следовательно:  .
. .
. , то существует
, то существует  , где
, где  .
. определены в некотором множестве X.
определены в некотором множестве X. из некоторого промежутка, содержащего точку
из некоторого промежутка, содержащего точку  выполняются неравенства
выполняются неравенства  и
и  имеют одинаковые пределы при
имеют одинаковые пределы при  тогда функция
тогда функция  имеет тот же предел при
имеет тот же предел при  .
.
 (первый замечательный предел).
(первый замечательный предел).

 ,
, ,
, ,
, ,
, .
. и
и  имеют в точке
имеют в точке  равный единице предел, то в силу теоремы 19.5:
равный единице предел, то в силу теоремы 19.5: , т.е. 1 – правый предел.
, т.е. 1 – правый предел. – четная функция, то
– четная функция, то  .
. .
. .
. – второй замечательный предел.
– второй замечательный предел. – бесконечно малая функция, если
– бесконечно малая функция, если  .
. .
.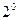 . Сумма и произведение конечного числа бесконечно малых функций при
. Сумма и произведение конечного числа бесконечно малых функций при  является бесконечно малой функцией при
является бесконечно малой функцией при  . Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.
. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция. – бесконечно большая функция при
– бесконечно большая функция при 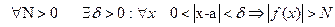 .
. .
.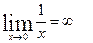 .Доказать, что
.Доказать, что  – бесконечно большая функция.
– бесконечно большая функция.
 называются неопределенностью.
называются неопределенностью. и
и 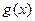 , заданные в проколотой окрестности точки
, заданные в проколотой окрестности точки  (
(  ).
).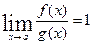 , то говорят, что
, то говорят, что 
 .
. ,то говорят, что они бесконечно малые (бесконечно большие) функции одного порядка.
,то говорят, что они бесконечно малые (бесконечно большие) функции одного порядка. и
и  , то говорят, что
, то говорят, что  – бесконечно малая функция более высокого порядка, чем
– бесконечно малая функция более высокого порядка, чем  .
.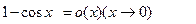
 определена в проколотой окрестности точки а(
определена в проколотой окрестности точки а(  ). Тогда, если существует
). Тогда, если существует  и существует
и существует  , то существуют
, то существуют  ,
,  и они равны предыдущим.
и они равны предыдущим. , тогда
, тогда .
. .
. .
.