 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Классификация элементарных функций
Лекция 18 Число е Рассмотрим последовательность {xn} с общим членом Докажем, что она сходится. Для этого достаточно доказать: 1) {xn} возрастающая; 2) {xn} ограничена сверху. Рассмотрим Докажем, что она сходится. Доказательство
Замечание1. Неравенство (*) верно: знаменатель увеличили, дробь уменьшилась. Обозначим
Итак, Так как
Замечание2. В доказательстве использовалась формула суммы бесконечно убывающей геометрической последовательности:
Обозначим
Таким образом
Функции одной переменной
Понятие функции Определение 18.1. Пусть x и y – некоторые числовые множества. Если каждому элементу множества X единственным образом соответствует элемент множества Y, то это соответствие называется функцией. Обозначение: Здесь y – зависимая переменная, х – независимая переменная (аргумент) X – обл. определения (существования) функции (D(f)); Y – множество значений функции (E(f)).
Определение 18.2. Пусть f(x) определена на некотором множестве X. f(x) ограничена сверху (снизу), если:
Условие ограниченности: Пример 18.1. Показать, что (
Способы задания функции 18.2.1. Аналитический При аналитическом способе задания функция задается с помощью формул: А) в явном виде Функция разрешена относительно y: Б) в неявном виде Функция не разрешена относительно y:
В некоторых случаях от неявно заданной функции можно перейти к явному виду, иногда это сделать невозможно: Пример 18.2.
При аналитическом способе функцию можно задать: а) несколькими выражениями:
Пример 18.3. б) параметрически:
Пример 18.4.
в) в полярной системе координат:
Пример 18.5.
18.2.2. Табличный
(Например, расписание поездов).
18.2.2. Графический Соответствие между аргументом и функцией задается посредством графика.
Замечание. Окружность, заданная формулой
Классификация элементарных функций Основные элементарные функции а) тригонометрические:
б) обратные тригонометрическим:
в) степенная: г) показательная: д) логарифмическая: Все функции, получаемые с помощью конечного числа арифметических действий над элементарными функциями, а также суперпозицией (или наложением) этих функций составляют класс элементарных функций. Пример 18.6. Примеры элементарных функций:
Классификация элементарных функций
Предел функции 18.3.1. Предел функции в точке
Определение 18.3. (на языке последовательностей) Пусть функция f(x) определена на множестве X. Пусть также заданы: последовательность а также соответствующая последовательность Или: Пример 18.7. Доказать, что функция Построим Но если построить
Таким образом, для двух сходящихся последовательностей, соответствующие последовательности значений функции имеют разные пределы. Определение 18.3 (предела функции в точке на языке эпсилон-дельта ( Число A называется пределом функции f(x) в точке Или : Замечание 3. Оба определения предела функции эквивалентны.
Геометрический смысл понятия «предел функции» Пусть М – произвольные точки графика функции Точки М графика должны находиться в полосе шириной
Пример 18.8.
Односторонние пределы Определение 18.4. Если у любой сходящейся к точке Обозначение: Определение 18.5. Если у любой сходящейся к Обозначение: Утверждение. Функция
Пример 18.9.
1)
2)
Поиск по сайту: |
 .
. и докажем, что последовательность {yn} убывает, т.е
и докажем, что последовательность {yn} убывает, т.е  .
.
 .
.

 , т.е. последовательность {yn} убывающая.
, т.е. последовательность {yn} убывающая. , то последовательность ограничена, т.е. существует предел последовательности
, то последовательность ограничена, т.е. существует предел последовательности  .
.
 …
… .
.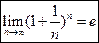 называют вторым замечательным пределом
называют вторым замечательным пределом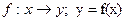 .
. .
. .
.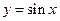 – ограниченная функция.
– ограниченная функция. ).
). .
. .
. .
. Signum (лат.)-знак.
Signum (лат.)-знак. .(график функции – астроида)
.(график функции – астроида) – уравнение лемнискаты Бернулли.
– уравнение лемнискаты Бернулли.







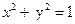 , не является графиком функции (это график уравнения), однако полуокружности, заданные уравнениями
, не является графиком функции (это график уравнения), однако полуокружности, заданные уравнениями  , являются графиками функций.
, являются графиками функций. ;
; ;
; ;
; ;
; .
. .
. . Функция вида
. Функция вида  , где
, где  называется целой рациональной функцией или алгебраическим многочленом степени
называется целой рациональной функцией или алгебраическим многочленом степени  .
. . Функция вида
. Функция вида  называетсядробно-рациональной.
называетсядробно-рациональной. . Функция, полученная с помощью конечного числа суперпозиций и арифметических действий над степенными функциями, не являющаяся рациональной, называется иррациональной функцией:
. Функция, полученная с помощью конечного числа суперпозиций и арифметических действий над степенными функциями, не являющаяся рациональной, называется иррациональной функцией:
 ,
, 
 . Функция, не являющаяся рациональной или иррациональной, называется трансцендентнойфункцией:
. Функция, не являющаяся рациональной или иррациональной, называется трансцендентнойфункцией: .
. .
. причем
причем 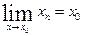 ,
, причем
причем 
 тогда
тогда  .
.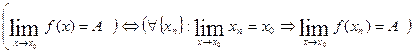 .
. не имеет предела.
не имеет предела. при
при 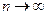 . Тогда
. Тогда  .
. , при
, при  , но
, но
 ))
)) , если:
, если: удовлетворяющих неравенству
удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. .
.
 .
. , ограниченной прямыми
, ограниченной прямыми  ,
,  , для всех значений x, удаленных от точки
, для всех значений x, удаленных от точки  не далее чем на
не далее чем на  .
.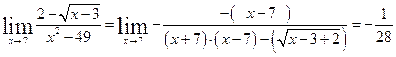 .
. все ее элементы меньше
все ее элементы меньше  сходится к
сходится к  , то число
, то число  .
.  .
. все ее элементы больше
все ее элементы больше  , то число
, то число  .
. .
. . Найти
. Найти  .
.
 .
. .
.