 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методические указания. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9 По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ Наименование работы: ИНТЕГРИРОВАНИЕ ЗАМЕНОЙ ПЕРЕМЕННОЙ И ПО ЧАСТЯМ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ. ВЫЧИСЛЕНИЕ ПЛОЩАДИ, ОБЪЕМА С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск 2012 г. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9 По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (2 курс) Наименование работы: ИНТЕГРИРОВАНИЕ ЗАМЕНОЙ ПЕРЕМЕННОЙ И ПО ЧАСТЯМ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ. ВЫЧИСЛЕНИЕ ПЛОЩАДИ, ОБЪЕМА С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ. 1. Цель работы:Приобретение навыков интегрирования заменой переменной и по частям в определенном интеграле. Приобретение навыков использования определенного интеграла для вычисления площадей плоских фигур, объемов тел вращения, вычисление несобственных интегралов с бесконечными пределами, интегралов от разрывных функций. 2. Литература: 2.1. В.А. Подольский, А.М. Суходольский "Сборник задач по математике" гл.12 §1-7 М.: Высшая школа, 1978 г. 2.2. Г.М. Гусак, Д.А. Капуцкая “Математика для подготовительных курсов” гл.11 §4-6 Минск: Высшая школа, 1989 г. 3. Подготовка к работе: 3.1. Изучить теоретический материал по теме: «Интегрирование заменой переменной и по частям в определенном интеграле. Вычисление площади, объема с помощью определенного интеграла. Вычисление несобственных интегралов». 3.2. Подготовить бланк отчета по практической работе. 3.3. Подготовить ответы на вопросы допуска к работе: 3.3.1. Понятие первообразной. 3.3.2. Понятие определенного интеграла. 3.3.3. Формула интегрирования заменой переменной и по частям. 3.3.4. Геометрический смысл определенного интеграла функции f(x) на отрезке. 3.3.5. Понятие несобственного интеграла. 4. Основное оборудование: 4.1. Литература, конспект. 5. Задание: 5.1. См.приложение. 6. Порядок выполнения работы: 6.1. Записать задание своего варианта в отчет. 6.2. Выполнить задание, согласно своему варианту. 6.3. Записать ответы, оформить отчет. 6.4. Подготовить ответы на контрольные вопросы. 7. Содержание отчета: 7.1. Титульный лист. 7.2. Цель работы. 7.3. Результаты и ход выполнения работы. 7.4. Выводы, ответы. 8. Контрольные вопросы: 8.1. Понятие первообразной. 8.2. Понятие определенного интеграла. 8.3. Свойства определенного интеграла. 8.4. Формула интегрирования заменой переменной. 8.5. Формула интегрирования по частям. 8.6. Геометрический смысл определенного интеграла функции f(x) на отрезке [a,b]. 8.7. Формула вычисления объема тела вращения вокруг оси OX, вокруг оси OY. 8.8. Понятие несобственного интеграла с бесконечным низшим (верхним) пределом, с двумя бесконечными пределами. 8.9. Понятие несобственного интеграла от разрывной функции. 8.10. Сходимость несобственных интегралов. 9. Приложение: Вариант 1 1. Вычислите определение интегралы: а) 2. Вычислить площадь плоской фигуры, ограниченной линиями y = x 3. Найти несобственный интеграл Вариант 2 1. Вычислите определение интегралы: а) 2. Вычислить площадь плоской фигуры, ограниченной линиями y=е 3. Найти несобственный интеграл
Вариант 3 1. Вычислите определение интегралы: а) 2. Вычислить площадь плоской фигуры, ограниченной линиями y = - 3. Найти несобственный интеграл Вариант 4 1. Вычислите определение интегралы: а) 2. Вычислить площадь плоской фигуры, ограниченной линиями y= sinx; x = - 3. Найти несобственный интеграл Вариант 5 1. Вычислите определение интегралы: а) 2. Вычислить площадь плоской фигуры, ограниченной линиями y = lnx; x = 3. Найти несобственный интеграл Вариант 6 1. Вычислите определение интегралы: а) 2. Вычислить площадь плоской фигуры, ограниченной линиями y =6x - x 3. Найти несобственный интеграл
Дополнительное задание: Вычислить объем тела, полученного вращением плоской фигуры вокруг одной из осей координат у = x
Методические указания.
Поиск по сайту: |
 ; б)
; б)  .
.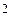 ; y = 9 (сделать чертеж).
; y = 9 (сделать чертеж).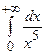 .
.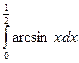 ; б)
; б)  .
. , x=0,5; x=1; y=0 (сделать чертеж).
, x=0,5; x=1; y=0 (сделать чертеж). .
.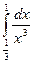 ; б)
; б)  .
. ; x = 1; x = 5 (сделать чертеж).
; x = 1; x = 5 (сделать чертеж). .
. ; б)
; б)  .
.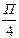 ; x =
; x =  ; y = 0 (сделать чертеж).
; y = 0 (сделать чертеж).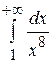 .
. ; б)
; б) 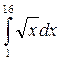 .
. ; x = е; y = 0 (сделать чертеж).
; x = е; y = 0 (сделать чертеж). .
. ; б)
; б)  .
. .
. , ось OX (сделать чертеж).
, ось OX (сделать чертеж).