 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Простейшие дроби и их интегрирование
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8 По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ Наименование работы: ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ И ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск 2012 г. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8 По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (2 курс) Наименование работы: ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ И ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ.
1. Цель работы:Приобретение навыков интегрирования функций, содержащих квадратный трехчлен, имеющих вид простейших рациональных дробей, использование при интегрировании разложение правильной рациональной дроби на сумму простейших дробей. 2. Литература: 2.1. В.А. Подольский, А.М. Суходольский "Сборник задач по математике" гл.11 §1-7 М.: Высшая школа, 1978 г. 3. Подготовка к работе: 3.1. Изучить теоретический материал по теме: «Интегрирование рациональных и иррациональных функций». 3.2. Подготовить бланк отчета по практической работе. 3.3. Подготовить ответы на вопросы допуска к работе. 4. Основное оборудование: 4.1. Литература, конспект. 5. Задание: 5.1. Вычислить неопределенные интегралы. 6. Порядок выполнения работы: 6.1. Учится интегрировать функции, содержащие квадратный трехчлен, имеющий вид простейших рациональных дробей. 6.2. Выполнять задания согласно варианту. 7. Содержание отчета: 7.1. Титульный лист. 7.2. Цель работы. 7.3. Условие, решение и ответ предложенного задания. 7.4. Ответы на контрольные вопросы. 8. Контрольные вопросы: 8.1. Принцип вычисления интеграла вида:
8.2. Разложение правильной рациональной дроби на слагаемые: 8.2.1 8.2.2. 8.3. Записать табличные интегралы вида: 9. Приложение: 9.1. Задания :
Методические указания. Простейшие дроби и их интегрирование. Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) – многочлены. Рациональная дробь называется правильной, если степень P(x) ниже степени Q(x); в противном случае дробь называется неправильной. Простейшими дробями 1, 2, 3, 4 типов называются правильные рациональные дроби следующего вида: 1. 2. 3. 4. Интегрирование простейших дробей 1 и 2 типов производится непосредственно:
Для интегрирования простейшей дроби 4 типа в числителе дроби нужно записать производную квадратного трехчлена и разложить полученный интеграл на сумму двух интегралов. Первый из них подстановкой x2 + px + q = t приведется к виду
Повторяя этот процесс, в конце концов получим интеграл
В практических вычислениях следует использовать не рекуррентную формулу, а метод, с помощью которого она выводится.
Поиск по сайту: |
 ;
; 
 ;
;
 ;
;
 .
.
 где
где  т. е. квадратный трехчлен не имеет действительных корней.
т. е. квадратный трехчлен не имеет действительных корней. где
где 
 2).
2). 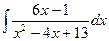
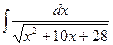 2).
2). 
 2).
2). 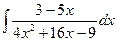
 2).
2). 
 2).
2). 
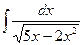 2).
2). 
 2).
2). 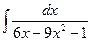
 2).
2).  2)
2) 

 , где m- целое число, большее единицы
, где m- целое число, большее единицы , т.е. квадратный трехчлен x2+px+q не имеет действительных корней.
, т.е. квадратный трехчлен x2+px+q не имеет действительных корней. , где n – целое число, большее единицы, и квадратный трехчлен x2 + px + q не имеет действительных корней.
, где n – целое число, большее единицы, и квадратный трехчлен x2 + px + q не имеет действительных корней.
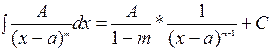
 , а второй имеет вид
, а второй имеет вид  . С помощью подстановки x + p/2 = u он преобразуется в интеграл вида
. С помощью подстановки x + p/2 = u он преобразуется в интеграл вида  , который интегрированием по частям можно свести к более простому интегралу
, который интегрированием по частям можно свести к более простому интегралу  того же типа, но показатель в знаменателе уменьшается на единицу. При этом справедлива формула:
того же типа, но показатель в знаменателе уменьшается на единицу. При этом справедлива формула:

