 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Затверджено на засіданні кафедри СТ
Затверджено на засіданні кафедри ІУС. Протокол № 1 від 31серпня 2011 р. Затверджено на засіданні кафедри СТ. Протокол № від 2011 р. "Узгоджено"
Завідувач кафедри ШІ ________________доц. Рябова Н.В. (підпис) (П.І.Б.)
Завідувач кафедри ІУС _________________проф. Левикін В.М. (підпис) (П.І.Б.)
Завідувач кафедри СТ _________________проф. Петров Е.Г. (підпис) (П.І.Б.)
Ухвалено вченою радою факультету КН Протокол №від “ ” 20 р.
Навчальний графік з дисципліни
"Математичні методи дослідження операцій " для напряму 6.050101 – “Комп’ютерні науки” (назва дисципліни, семестр, шифр потоку) 5-й семестр
2 МЕТА І ЗАВДАННЯ ДИСЦИПЛІНИ
2.1. Мета навчальної дисципліни
Вивчення загально-методологічних принципів побудови операційних моделей, основних етапів і сутності операційних досліджень і здатність їх застосовувати під час аналізу та синтезу інформаційних систем різного призначення та в завданнях організаційно-економічного управління.
2.2. Завдання дисципліни
За результатом вивчання дисципліни студенти повинні: ЗНАТИ: - загальну методологію та методику проведення дослідження операцій; - типові класи задач дослідження операцій; - математичні моделі оптимізаційних задач та класифікацію задач математичного програмування; - методи розв'язання лінійних оптимізаційних задач (графічні та аналітичні); - загальні методи розв'язання задач дискретного, параметричного, динамічного, стохастичного програмування; - математичний апарат розв'язання задач нелінійного програмування, основні алгоритми відшукання розв'язку; - основні методи оптимізації функцій, що диференцюються і що не диференцюються; - основні методи оптимізації в задачах великої розмірності; - основні задачі та методи багатокритеріальної оптимізації; - методи аналізу розв'язку задач оптимізації. ВМІТИ: - аналізувати та моделювати проблемні ситуації; - обгрунтовувати застосування методів оптимізації щодо розв'язання конкретних задач; - проводити геометричну інтерпретацію задач лінійного програмування; - розв'язувати лінійні оптимізаційні задачі за допомогою симплексного методу та його модифікацій; - розв'язувати лінійні оптимізаційні задачі (транспортні задачі) за допомогою спеціальних методів; - розв'язувати нелінійні задачі цілочислового програмування методом Гоморі та методом віток і меж; - здійснювати комп’ютерну реалізацію розв’язання задач лінійного програмування та багатокритеріальних оптимізаційних задач; - аналізувати розв'язки задач оптимізації.
3. ПЕРЕЛІК ЗАБЕЗПЕЧУЮЧИХ ДИСЦИПЛІН
4. ТЕМАТИЧНИЙ ПЛАН
4.1 Розподіл обсягу змістовних модулів за видами занять
4.2 Практичні заняття
4.3 Лабораторні роботи
4.4. Самостійна робота студента
4.4. Рейтингова оцінка за дисципліною
4.4.1 Кількісні критерії оцінювання
Як форма підсумкового контролю для дисципліни «Математичні методи дослідження операцій» використовується комбінований іспит. Рейтингова оцінка
При формуванні оцінок Для оцінювання роботи студента протягом семестру рейтингова оцінка Практичні заняття з урахуванням лекційного матеріалу і матеріалів самостійної роботи, оцінюються за 100-бальною системою. Кількість балів за кожне практичне заняття Лабораторні роботи з урахуванням лекційного матеріалу і матеріалів самостійної роботи, також оцінюються за 100-бальною системою. Кількість балів за кожну лабораторну роботу
Таблиця «Рейтингова оцінка за дисципліною»
При цьому виді контролю підсумкова оцінка Комбінований іспит передбачає поєднання таких видів роботи як письмову відповідь на екзаменаційний білет та усну відповідь. Білет для комбінованого іспиту складається з двох теоретичних запитань та одного практичного завдання. Теоретичні запитання оцінюються за 100-бальною шкалою у 35 балів кожне і практичне завдання – в 30 балів. Питання з самостійної роботи над дисципліною (опрацювання матеріалу додаткової літератури тощо) введені в теоретичну частину іспиту у вигляді теоретичних запитань. Рейтингова оцінка в діапазоні [60-100] вважається позитивною, а в діапазоні [1-59] – незадовільною і підлягає перездачі.
4.4.2 Якісні критерії оцінювання
4.4.2.1 Необхідний обсяг знань для одержання позитивної оцінки
1. Побудова математичних моделей проблемних ситуацій. Загальна методологія та методика проведення дослідження операцій. Типові класи задач дослідження операцій. Загальна математична модель оптимізаційних задач. 2. Задачі математичного програмування (МП). Загальна постановка задачі МП. Класифікація задач МП. 3. Лінійне програмування. Задачі лінійного програмування (ЗЛП). Постановка та форми запису ЗЛП. Приклади практичних задач лінійного програмування. 4. Геометрична інтерпретація ЗЛП. Симплексний метод розв'язування ЗЛП. Основні ЗЛП з штучною базою. М-задача. Двоїстий симплекс-метод. 5. Двоїстість. Двоїстість (спряженість) у лінійному програмуванні. Основні теореми двоїстості та їх економічний зміст. 6. Спеціальні задачі МП. Транспортна задача (Т-задача) та її математична модель. Методи визначення опорного плана. Метод потенціалів. 7. Постоптимальний аналіз. 8. Основні положення параметричного програмування. 9. Нелінійне програмування. Класичні методи оптимізації. ЗНП за умови невід’ємності змінних. Умови Куна-Таккера для ЗНП. 10. Задача квадратичного програмування (ЗКП). Метод і алгоритм Франка-Вулфа. 11. Основні положення сепарабельного програмування. Визначення сеперабельної функції. Метод кусково-лінійної апроксімації. Задачі дробово-лінійного (гіперболічного) програмування 12. Основні положення дискретного програмування. Загальні характеристика дискретних задач. Спеціальні методи вирішення задач дискретного програмування. Клас цілочислових лінійних задач. Метод відсікань (метод Гоморі) розв’язання ЗЦЛП. Метод гілок та меж в задачах цілочислового програмування. 13. Основні положення динамічного програмування. Загальна структура задач динамічного програмування. Задачі розподілу ресурсів. 14. Основні положення стохастичного програмування. Методи розв’язання задач стохастичного програмування. 15. Методи оптимізації функцій, що диференцюються. Методи оптимізації функцій, що не диференцюються. 16. Методи оптимізації в задачах великої розмірності. Задачі та методи багатокритеріальної оптимізації.
4.4.2.2 Необхідний обсяг умінь для одержання позитивної оцінки
1. Уміти аналізувати та моделювати проблемні ситуації, що виникають під час аналізу та синтезу інформаційних систем різного призначення та в завданнях організаційно-економічного управління. 2. Уміти обгрунтовувати застосування методів оптимізації щодо розв'язання конкретних задач. 3. Уміти зводити до канонічної форми загальну задачу лінійного програмування і зводити до стандартної форми канонічну задачу лінійного програмування. 4. Уміти проводити геометричну інтерпретацію задач лінійного програмування. 5. Уміти розв'язувати задачі лінійного програмування за допомогою симплексного методу та його модифікацій. 6. Уміти розв'язувати лінійні оптимізаційні задачі (транспортні задачі) за допомогою методу потенціалів. 7. Уміти розв'язувати нелінійні задачі цілочислового програмування методом Гоморі та методом віток і меж. 8. Уміти вирішувати задачу розподілу ресурсів. 9. Уміти здійснювати комп’ютерну реалізацію розв’язування задач лінійного програмування та багатокритеріальних оптимізаційних задач. 10. Уміти аналізувати розв'язки задач оптимізації.
4.4.2.3 Критерії оцінювання роботи студента протягом семестру
Задовільно, D, E (60-74). Оцінку «задовільно» заслуговує студент, який виявив мінімум знання основного змісту матеріалу з дисципліни в об’ємі, необхідному для подальшого навчання й майбутньої роботи за напрямом (спеціальністю), який справився з виконанням усіх практичних занять, лабораторних робіт і контрольної роботи, що передбачені програмою, але у звітах, результатах домашніх і аудиторних робіт, а також відповідях на запитання є похибки. Добре, С (75-89). Оцінку «добре» заслуговує студент, який виконав усі домашні завдання, відпрацював всі практичні заняття і лабораторні роботи, виконав контрольну роботу (аудиторну), який виявив повне знання програмного матеріалу, вірно розкрив суть проблем та у цілому розв’язав завдання практичних занять і лабораторних робіт, але у змісті відповіді є незначні помилки, або недостатньо обґрунтовано надані відповіді на запропоновані запитання з лекційного матеріалу з дисципліни, з матеріалу практичних занять, лабораторних робіт та матеріалу з самостійної роботи. Відмінно, А, В (90-100). Оцінку «відмінно» заслуговує студент, який виявив всебічні чіткі, систематичні та глибокі знання теоретичного та практичного навчального матеріалу з дисципліни, вірно розкрив суть і достатньо обґрунтував своє ставлення до запропонованих питань, виявив вміння вільно виконувати практичні завдання (і лабораторні роботи), що передбачені програмою, а також безпомилково виконав вправи, вміє аналізувати і систематизувати інформацію.
5. НАВЧАЛЬНО–МЕТОДИЧНІ МАТЕРІАЛИ З ДИСЦИПЛІНИ (Дисципліна вивчається з 1995 р.)
5.1. Основна література
1. Бондаренко, М.Ф. Оптимізаційні задачі в системах прийняття рішень [Текст] : підручник / М.Ф. Бондаренко, А.М. Гвоздинський. – Харків: ХТУРЕ, 1998. – 216 с. 2. Гвоздинський, А.М. Методи оптимізації в системах прийняття рішень [Текст] : навч. посібник / А. М. Гвоздинський, Н. А. Якімова, В. О. Губін. – Харків: ХНУРЕ, 2006, – 325 с. 3. Ларіонов, Ю.І. Дослідження операцій в інформаційних системах [Текст] : навч. посібник / Ю. І. Ларіонов, В. М. Левикін, М. А. Хажмурадов. –Харків: Компанія СМІТ, 2005. – 364 с. 4. Гвоздинський, А.М. Оптимізаційні задачі в організаційному управлінні. Частина 1. Детерміновані моделі [Текст] : навч. посібник / А. М. Гвоздинський. – Харків: ХТУРЕ, 1997. – 116 с. 5. Гвоздинський, А.М. Оптимізаційні задачі в організаційному управлінні. Частина 2. ігрові моделі [Текст] : навч. посібник / А. М. Гвоздинський. – Харків: ХТУРЕ, 1997. – 56 с. 6. Гвоздинський, А.М. Оптимізаційні задачі в організаційному управлінні. Частина 3. Мережні моделі [Текст] : навч. посібник / А.М. Гвоздинський, В.О. Губін, Є.П. Павленко. – Харків: ХТУРЕ, 1997. – 112 с. 7. Вентцель, Е.С. Исследование операций [Текст] / Е. С. Вентцель. – М.: Высш.шк., 2000. – 552 с.
5.2. Додаткова література
8. Ульянченко, О.В. Сучасні моделі дослідження операцій в економіці [Текст] : навч. посібник / О. В. Ульянченко; Харк. держ. аграр. ун-т ім. В. В. Докучаєва. – Харків, 2000. – 141 с. 9. Ларіонов, Ю.І. Дослідження операцій та математичні методи. Частина 1. Методологія дослідження операцій. Лінійне програмування [Текст] : навч. посібник / Ю. І. Ларіонов, В. М. Левикін, М. А. Хажмурадов. –Харків: ХТУРЕ, 1999. – 124 с. 10. Ларіонов, Ю.І. Короткий тлумачний словник із системного аналізу і дослідження операцій. Основні терміни [Текст] : навч. посібник / Ю. І. Ларіонов. – К.: ІСДО, 1994. – 96 с. 11. Акулич, И.Л. Математическое программирование в примерах и задачах [Текст] / И. Л Акулич. – М.: Высш.шк., 1986. – 319 с. 12. Зайченко, Ю.Л. Исследование операций [Текст] : учебник / Ю. Л. Зайченко, С. А. Шумилова. – К.: Вища школа, 1984. – 224 с. 13. Єрмольєв, Ю. М. Математичні методи дослідження операцій [Текст] : навч. посібник / Ю.М. Єрмольєв, І.І. Ляшко. – К.: Вища школа, 1979. – 312 с.
5.3. Методичні посібники та вказівки
14. Методичні вказівки до практичних занять з дисциплін «Математичні методи дослідження операцій», «Дослідження операцій» [Текст] / Упоряд.: А .М. Гвоздинський, В. О. Губін, В. Л. Шергін. – Харків: ХНУРЕ, 2009. – 36 с. 15. Методичні вказівки до лабораторних робіт з дисципліни «Математичні методи дослідження операцій» [Текст] / Упоряд.: А. М. Гвоздинський, В. О. Губін. – Харків: ХНУРЕ, 2011. – 20 с. 16. Методичні вказівки до самостійної роботи з дисципліни «Математичні методи дослідження операцій» для студентів усіх форм навчання напряму 6.050101 – «Комп’ютерні науки» [Текст] / Упоряд.: А. М. Гвоздинський, В.О. Губін, В.Л. Шергін. – Харків: ХНУРЕ, 2010. – 24 с. 17. Методичні вказівки до виконання контрольної роботи з дисципліни «Математичні методи дослідження операцій» [Текст] / Упоряд.: Ю.І. Ларіонов, В.М. Левикін, М.А. Хажмурадов. – Харків: ХНУРЕ, 2008. – 52 с.
5.4 Програмне забезпечення ЕОМ з дисципліни
1. Системне програмне забезпечення: операційні системи Windows 2000, ХР. 2. Прикладне програмне забезпечення: ППП для реалізації симплексного методу; ППП для розв’язання Т-задач; ППП для розв’язання ЗЛП.
6. ПИТАННЯ ОХОРОНИ ПРАЦІ ПРИ ВИВЧЕННІ ДИСЦИПЛІНИ
1. Проведення інструктажів з охорони праці та безпеки життєдіяльності на початку роботи з групами студентів. Розглядання питань щодо правових, соціально-економічних, організаційно-технічних, санітарно-гігієнічних заходів з охорони праці студентів у процесі навчання у вищому навчальному закладі.
Доповнення та зміни у робочій програмі
Перелік деталізованих компетенцій
Доповнення до робочої програми підготував______________________________________________ (підпис, посаду, прізвище, ініціали)
"Узгоджено" Зав.кафедрою ______________________ (підпис, прізвище, ініціали)
Поиск по сайту: |
 сам. роб.
сам. роб.
 з дисципліни «Математичні методи дослідження операцій» має дві складові:
з дисципліни «Математичні методи дослідження операцій» має дві складові:  – кількість балів, отриманих студентом протягом семестру (максимальна рейтингова оцінка протягом семестру – 100 балів) та
– кількість балів, отриманих студентом протягом семестру (максимальна рейтингова оцінка протягом семестру – 100 балів) та  – кількість балів, отриманих студентом на іспиті (максимальний бал також становить 100) і формується у такий спосіб:
– кількість балів, отриманих студентом на іспиті (максимальний бал також становить 100) і формується у такий спосіб: .
.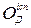 ,
, 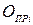 складається з балів
складається з балів  , якими оцінюється присутність і відпрацювання практичного заняття, а також з балів
, якими оцінюється присутність і відпрацювання практичного заняття, а також з балів  , якими оцінюється виконання домашнього завдання з кожного практичного заняття, тобто
, якими оцінюється виконання домашнього завдання з кожного практичного заняття, тобто  .
. складається з балів
складається з балів  , якими оцінюється присутність і відпрацювання лабораторної роботи, а також з балів
, якими оцінюється присутність і відпрацювання лабораторної роботи, а також з балів  , якими оцінюється захист звіту з лабораторної роботи, тобто
, якими оцінюється захист звіту з лабораторної роботи, тобто  . Оцінки за кожне практичне заняття
. Оцінки за кожне практичне заняття  ) наведені в таблиці «Рейтингова оцінка за дисципліною».
) наведені в таблиці «Рейтингова оцінка за дисципліною». , де
, де  -те практичне заняття;
-те практичне заняття; 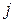 -ту лабораторну роботу;
-ту лабораторну роботу;