 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Зображення синусоїдних величин векторними
Згідно з першим законом Кірхгофа, для вузла (Рис. 4)
При відомих струмах Значно простішими обчислення будуть при заміні синусоїд векторами. Миттєві значення функції
У момент Таким чином, розгляд синусоїдних функцій можна замінити розглядом обертових векторів, а для одержання миттєвих значень потрібно взяти проекцію векторів на вертикальну вісь. Будь-якому обертовому вектору можна поставити у відповідність синусоїду і, навпаки, будь-якій синусоїді можна поставити у відповідність обертовий вектор, а кут відраховувати від горизонтальної осі. Якщо синусоїдні функції мають однакову частоту то відповідні їм вектори обертаються з однаковою кутовою швидкістю, а тому кути між ними незмінні. Отже: якщо в електричному колі протікають синусоїдні струми і діють синусоїдні напруги однієї частоти, то у цьому випадку обертову систему векторів, що зображають синусоїди, можна зупинити (зафіксувати), тому що при обертанні кути між векторами не змінюються. На Рис. 6 зображені вектори
Як відомо з математики, проекція геометричної суми векторів на будь-яку вісь дорівнює алгебраїчній сумі проекцій цих векторів на ту ж вісь. Тобто алгебраїчному додаваню миттєвих значень синусоїд відповідає геометричне додавання зображаючих їх векторів. Векторна діаграма найбільш наочно показує співвідношення амплітуд та кути зсуву фаз між синусоїдними напру-гами і струмами.
Додатнім (напруга випереджає струм) вважається кут зсуву фаз
Векторні діаграми будуються як для амплітуд, так і для діючих значень, в останньому випадку модулі векторів зменшуються в порівнянні з амплітудами в
Поиск по сайту: |
 .
.
 ,
,  струм і1 можна знайти графічно, складаючи ординати синусоїд, і1=
струм і1 можна знайти графічно, складаючи ординати синусоїд, і1=  + +
+ +  =
=  , але це викликає значні труднощі при по-будові.
, але це викликає значні труднощі при по-будові. можна одержати як проекцію на вертикальну вісь відрізка довжиною Im (Рис. 5), який обертається відносно початку прямокутної системи координат з кутовою швидкістю
можна одержати як проекцію на вертикальну вісь відрізка довжиною Im (Рис. 5), який обертається відносно початку прямокутної системи координат з кутовою швидкістю  у пози-тивному напрямку (тобто проти годинникової стрілки). Цей відрізок називають умовним обертовим вектором.
у пози-тивному напрямку (тобто проти годинникової стрілки). Цей відрізок називають умовним обертовим вектором.
 вектор розміщений під кутом
вектор розміщений під кутом  до горизонтальної осі і його проекція на вертикальну вісь дорівнює
до горизонтальної осі і його проекція на вертикальну вісь дорівнює  , тобто митттєвому значенню заданої функції при
, тобто митттєвому значенню заданої функції при  вектор повернеться на кут
вектор повернеться на кут  і буде повернутий відносно горизонтальної осі на кут
і буде повернутий відносно горизонтальної осі на кут  , а його проекція на вер-тикальну вісь буде
, а його проекція на вер-тикальну вісь буде  і т.д.
і т.д.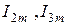 зі своїми кутами
зі своїми кутами 
 та їх сума
та їх сума  з кутом
з кутом  . Діаграма, на якій показані вектори, що зображають синусоїдні напруги і струми з урахуванням зсуву фаз між ними називається векторною діаграмою.
. Діаграма, на якій показані вектори, що зображають синусоїдні напруги і струми з урахуванням зсуву фаз між ними називається векторною діаграмою.
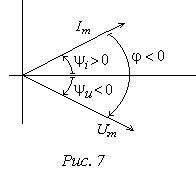
 (відраховуєть-ся від горизонтальної осі проти годиннико-вої стрілки), кут
(відраховуєть-ся від горизонтальної осі проти годиннико-вої стрілки), кут  (відраховується за годинниковою стрілкою). Кут зсуву фаз
(відраховується за годинниковою стрілкою). Кут зсуву фаз  - (струм випереджає напру-гу).
- (струм випереджає напру-гу).
 , що від-раховується від струму до напруги по найкоротшому шляху проти годиннико-вої стрілки (Рис. 8, а), у протилежному випадку кут j - від’ємний (Рис. 8, б).
, що від-раховується від струму до напруги по найкоротшому шляху проти годиннико-вої стрілки (Рис. 8, а), у протилежному випадку кут j - від’ємний (Рис. 8, б).
 раз.
раз.