 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Зведення сил інерції точок твердого тіла до найпростішого вигляду при поступальному, обертальному та плоскопаралельному русі
І. Поступальний рух тіла. При поступальному русі твердого тіла всі його точки мають геометрично рівні швидкості і прискорення, які дорівнюють швидкості і прискоренню центра мас. Приймемо центр мас тіла за центр зведення сил інерції. Оскільки обертання тіла навколо центра мас не відбувається, то головний вектор-момент сил інерції відносно центра мас дорівнюватиме нулю, тобто Отже, при поступальному русі твердого тіла сили інерції його точок зводяться до рівнодійної, що дорівнює головному вектору, яка прикладена в центрі мас тіла та має напрям, протилежний до напряму вектора прискорення:
ІІ. Обертання тіла, що має площину матеріальної симетрії, навколо нерухомої головної центральної осі. В цьому випадку центр мас тіла лежить на осі обертання і є нерухомим, тобто його прискорення
Кінетичний момент тіла, що обертається відносно осі обертання, дорівнює:
При цьому головний вектор – момент сил інерції дорівнюватиме:
або
Отже, при обертанні твердого тіла навколо головної центральної нерухомої осі сили інерції точок тіла зводяться до пари сил, що лежить в площині матеріальної симетрії, а вектор – момент цієї пари дорівнює добутку момента інерції тіла на вектор кутового прискорення і має напрям, протилежно до напряму вектора кутового прискорення.
ІІІ. Плоскопаралельний рух твердого тіла, що має площину матеріальної симетрії. Нехай тіло, що має площину матеріальної симетрії, рухається так, що всі його точки рухаються паралельно до цієї площини (рис. 11.1). Цей рух можна розкласти на поступальний разом із центром мас т. С і на обертальний рух навколо рухомої осі Як відомо, при поступальному русі сили інерції зводяться до головного вектора
Приклад. Кільце, радіуса
Враховуючи (11.3) маємо
Покажемо на рисунку їх напрямки. За модулем Тоді остаточно маємо 11.2. Визначення додаткових динамічних реакцій при русі зв’язаної механічної системи. При русі невільної і-ої матеріальної точки повні реакції в’язей
Аналогічну рівність задовольняють також головні вектори і головні моменти реакцій в’язей при русі зв’язаного твердого тіла
При цьому статичні реакції задовольняють такі шість рівнянь:
Підставимо в рівняння кінетостатики (31.7) величини проекцій головного вектора
Враховуючи в системі рівнянь (11.6) відповідно шість рівнянь (11.5), яким задовольняють статичні реакції, дістанемо рівняння для визначення додаткових динамічних реакцій опор рухомого твердого тіла:
Зазначимо, що при складанні рівнянь (11.7) не потрібно враховувати активні сили. Отже, одним з найпростіших методів визначення додаткових динамічних реакцій є метод кінетостатики.
Поиск по сайту: |
 .
. . (11.1)
. (11.1) , тоді:
, тоді: .
.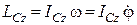 .
.
 .(11.2)
.(11.2) , яка перпендикулярна до площини симетрії і проходить через центр мас.
, яка перпендикулярна до площини симетрії і проходить через центр мас. , а при обертальному русі навколо головної центральної осі сили інерції зводяться до пари сил з вектором-моментом
, а при обертальному русі навколо головної центральної осі сили інерції зводяться до пари сил з вектором-моментом  , тобто тут маємо два фактори сил інерції:
, тобто тут маємо два фактори сил інерції: . (11.3)
. (11.3) Отже, при русі твердого тіла, що має площину матеріальної симетрії, паралельно до цієї площини, сили інерції точок тіла зводяться до однієї сили, що лежить в площині матеріальної симетрії, яку прикладено в центрі мас, що дорівнює головному вектору сил інерції
Отже, при русі твердого тіла, що має площину матеріальної симетрії, паралельно до цієї площини, сили інерції точок тіла зводяться до однієї сили, що лежить в площині матеріальної симетрії, яку прикладено в центрі мас, що дорівнює головному вектору сил інерції  і маси
і маси  , котиться без ковзання за прямолінійною дорогою, маючи в даний момент часу швидкість центра
, котиться без ковзання за прямолінійною дорогою, маючи в даний момент часу швидкість центра  та прискорення
та прискорення  (рис. 11.2). Знайти два фактори сил інерції, які діють на колесо в даний момент часу.
(рис. 11.2). Знайти два фактори сил інерції, які діють на колесо в даний момент часу. Розвязання. Точка дотику колеса і поверхні т.Р –МЦШ. Тоді
Розвязання. Точка дотику колеса і поверхні т.Р –МЦШ. Тоді  . Т.С – центр мас колеса.
. Т.С – центр мас колеса. та
та 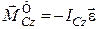 .
. і
і  , де
, де  .
. .
. складаються з статичних реакцій
складаються з статичних реакцій  і додаткових динамічних реакцій
і додаткових динамічних реакцій  :
: .
. ;
;  . (11.4)
. (11.4) ;
; 

 ;
;  ;
;  . (11.5)
. (11.5) і головного момента
і головного момента  реакцій в’язей, визначених рівністю (11.4):
реакцій в’язей, визначених рівністю (11.4): ;
;  ;
; ;
;  ; (11.6)
; (11.6) ;
;  .
. ;
;  ;
; ;
;  ; (11.7)
; (11.7) ;
;  .
.