 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Принцип Д’Аламбера для механічної системи
ПРИНЦИПИ МЕХАНІКИ
Принцип Д’Аламбера для матеріальної точки Розглянемо рух невільної матеріальної точки під дією заданих сил. Векторне рівняння руху цієї точки з урахуванням реакцій в’язей має вигляд:
Тут Якщо
Введемо таке позначення : Вектор сили Враховуючи (10.2), рівняння (10.1) набуває вигляду:
Вектор сили Рівняння (10.3) являє собою принцип Д’Аламбера для матеріальної точки: Якщо до рухомої невільної матеріальної точки умовно прикласти її силу інерції, тоді геометрична сума заданих сил, реакцій в’язей і умовно прикладеної сили інерції дорівнюватиме нулю. Отже, за допомогою принципу Д’Аламбера рівнянням динаміки можна надати форми рівнянь статики (іншими словами, задачі динаміки можна розв’язувати методами статики). Такий метод складання рівнянь руху має назву метода кінетостатики і широко застосовується в інженерних розрахунках при визначенні динамічних реакцій опор твердих тіл. Властивостідаламберової сили інерції 1) Це – сила фіктивна. Вона, на відміну від фізичних сил, не має свого джерела виникнення. Фізично даламберових сил інерції в дійсності не існує. 2) Третій закон Ньютона (рівності дії і протидії) на неї не поширюється. 3) Прикладається умовно, штучно, щоб надати рівнянням руху вигляд рівнянь рівноваги. Принцип Д’Аламбера для механічної системи Розглянемо рух невільної механічної системи, що складається з Застосуємо метод кінетостатики, а попередньо, принцип звільнення від в’язей до кожної точки системи, що розглядається:
Тут Рівняння (10.4) являють собою принцип Д’Аламбера для механічноїсистеми, який формулюється так: В рухомій невільній механічній системі в будь-який момент часу для кожної матеріальної точки системи геометрична сума прикладених до неї внутрішніх, зовнішніх сил, реакцій в’язей та її сили інерції дорівнює нулю. Покажемо, що з принципу Д’Аламбера для механічної системи можна отримати два векторних або шість аналітичних рівнянь, які дозволяють розв’язувати задачі динаміки методами статики. Підсумовуючи всі
або
Тут З рівняння (10.5) випливає: Для рухомої невільної механічної системи в будь-який момент часу геометрична сума головних векторів заданих сил, реакцій в’язей і сил інерції всіх точок цієї системи дорівнює нулю. Якщо векторно домножити радіус-вектор
або
Тут З рівняння (10.6) випливає: Для рухомої невільної механічної системи в будь-який момент часу сума головних векторів-моментів заданих сил, реакцій в’язей і сил інерції всіх точок системи відносно будь якого нерухомого центра дорівнює нулю. Проектуючи два векторні рівняння (10.5) і (10.6) на кожну з трьох координатних осей відповідно, отримаємо шість аналітичних рівнянь:
Якщо задана механічна система складається з кількох з’єднаних тіл, то рівняння (10.7) можна записати окремо для кожного тіла.
Поиск по сайту: |
 .
. – рівнодійна заданих сил,
– рівнодійна заданих сил,  – рівнодійна реакцій в’язей.
– рівнодійна реакцій в’язей. перенести в праву частину рівності, то матимемо:
перенести в праву частину рівності, то матимемо: . (10.1)
. (10.1) . (10.2)
. (10.2) який дорівнює добутку маси точки на вектор її прискорення називається даламберовою силою інерції і спрямований він протилежно до вектора прискорення.
який дорівнює добутку маси точки на вектор її прискорення називається даламберовою силою інерції і спрямований він протилежно до вектора прискорення. . (10.3)
. (10.3) матеріальних точок. В загальному випадку на кожну точку можуть діяти задані сили і реакції в’язей.
матеріальних точок. В загальному випадку на кожну точку можуть діяти задані сили і реакції в’язей.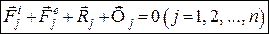 . (10.4)
. (10.4)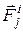 – рівнодійна всіх прикладених до точки внутрішніх сил;
– рівнодійна всіх прикладених до точки внутрішніх сил; 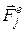 – рівнодійна всіх прикладених до точки зовнішніх сил;
– рівнодійна всіх прикладених до точки зовнішніх сил;  – рівнодійна реакцій в’язей, накладених на цю точку;
– рівнодійна реакцій в’язей, накладених на цю точку; 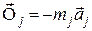 – сила інерції точки.
– сила інерції точки.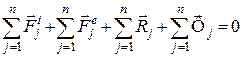 ,
,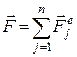 – головний вектор всіх зовнішніх сил;
– головний вектор всіх зовнішніх сил;  – головний вектор реакцій в’язей;
– головний вектор реакцій в’язей;  – головний вектор сил інерції всіх точок механічної системи. За першою властивістю внутрішніх сил механічної системи маємо
– головний вектор сил інерції всіх точок механічної системи. За першою властивістю внутрішніх сил механічної системи маємо  .
.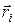 точки
точки  на кожне з співвідношень (10.4) і підсумувати всі
на кожне з співвідношень (10.4) і підсумувати всі 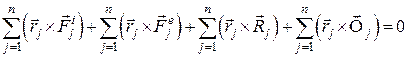
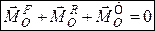 . (10.6)
. (10.6) – головний вектор-момент відносно центра
– головний вектор-момент відносно центра  всіх зовнішніх сил;
всіх зовнішніх сил;  – головний вектор-момент відносно центра
– головний вектор-момент відносно центра  – головний вектор-момент відносно центра О сил інерції всіх точок системи. За другою властивістю внутрішніх сил механічної системи маємо
– головний вектор-момент відносно центра О сил інерції всіх точок системи. За другою властивістю внутрішніх сил механічної системи маємо  (10.7)
(10.7)