ПЗУ как универсальная комбинационная микросхема

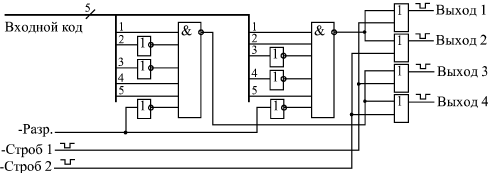
Одно из самых распространенных применений микросхем ПЗУ — замена ими сложных комбинационных схем. Такое решение позволяет существенно упростить проектируемое устройство и снизить количество используемых комбинационных микросхем, а иногда даже уменьшить потребляемый ток и увеличить быстродействие схемы.

Суть предлагаемого подхода сводится к следующему. Если рассматривать адресные входы микросхемы ПЗУ как входы комбинационной схемы, а разряды данных — как выходы этой комбинационной схемы, то можно сформировать любую требуемую таблицу истинности данной комбинационной схемы. Для этого всего лишь надо составить таблицу прошивки ПЗУ, соответствующую нужной таблице истинности. В этом случае не надо ни подбирать логические элементы, ни оптимизировать их соединения, ни думать о том, можно ли вообще построить заданную комбинационную схему из стандартных микросхем. Важно только, чтобы количество требуемых входов не превышало количества адресных разрядов ПЗУ, а количество требуемых выходов не превышало разрядности шины данных ПЗУ.

В качестве примера рассмотрим довольно сложную комбинационную схему (рис. 11.5), имеющую восемь входов и четыре выхода. Функция схемы сводится к следующему. Прежде всего она распознает два различных 5-разрядных входных кода (11001 и 10011) в случае, когда на входе разрешения "–Разр." присутствует нулевой сигнал, а при приходе сигналов "–Строб 1" и "Строб 2" схема выдает на выход отрицательные импульсы. Причем первый выходной сигнал вырабатывается в случае, когда входной код равен 11001 и пришел сигнал "–Строб 1", второй выходной сигнал — при том же коде, но по входному сигналу "–Строб 2". Третий и четвертый выходной сигналы вырабатываются при входном коде 10011 и при приходе соответственно управляющих сигналов "–Строб 1" и "–Строб 2". То есть логика работы довольно сложная и разнообразных логических элементов требуется немало.

Рис. 11.5. Пример комбинационной схемы, заменяемой ПЗУ

Рис. 11.6. Включение ПЗУ для замены комбинационной схемы, показанной на рис. 11.5

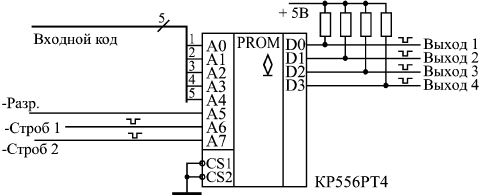
Но всю эту схему можно заменить всего лишь одной микросхемой ПЗУ, например, типа РТ4, имеющей 8 адресных входов и 4 выхода данных (рис. 11.6). При этом пять разрядов входного кода подаются на младшие разряды адреса ПЗУ (А0...А4), входной сигнал "Разр." — на адресный вход А5, сигнал "–Строб 1" — на вход А6, сигнал "–Строб 2" — на вход А7. Младший разряд данных памяти D0 используется для первого выходного сигнала, D1 — для второго выходного сигнала, D2 — для третьего выходного сигнала, D3 — для четвертого выходного сигнала. Микросхема ПЗУ всегда выбрана (управляющие сигналы –CS1 и –CS2 — нулевые). На выходах данных памяти включены резисторы, так как тип выходов микросхемы РТ4 — ОК.

Составим карту прошивки ПЗУ. Активные выходные сигналы — нулевые, а пассивные — единичные. Значит, в большинстве ячеек ПЗУ будут записаны коды F (все выходные сигналы пассивны). Активному (нулевому) первому выходному сигналу при пассивных остальных будет соответствовать двоичный код данных 1110 (16-ричный код — Е), активному второму выходному сигналу будет соответствовать двоичный код 1101 (16-ричный — D), активному третьему выходному сигналу — двоичный код 1011 (или В), активному четвертому выходному сигналу — двоичный код 0111 (или 7). То есть только содержимое четырех ячеек памяти будет отличаться от F.

Например, код Е будет записан в ячейку с таким адресом, пять младших разрядов которого (A0...А4) равны селектируемому входному коду 11001, разряд А5 равен нулю (сигнал "Разр." активен), разряд А6 равен нулю (сигнал "Строб 1" активен), а разряд А7 равен единице (сигнал "Строб 2" пассивен). Таким образом, получаем двоичный код адреса 10011001 (или в 16-ричном коде 99). Точно так же код D будет записан в ячейку с адресом 01011001 (то есть 16-ричное 59), код В — в ячейку с адресом 10010011 (то есть 93), а код 7 — в ячейку с адресом 01010011 (то есть 53). Получившаяся карта прошивки ПЗУ приведена в табл. 11.2. Она полностью совпадает с таблицей истинности заменяемой комбинационной схемы.

Может показаться, что такое использование микросхемы ПЗУ чересчур расточительно, избыточно, но это не так. Гораздо важнее, что схема сильно упрощается. Если же взять комбинационную схему с более сложной таблицей истинности, то возможности ПЗУ будут использованы полнее. К тому же большое достоинство такого решения состоит в том, что при необходимости изменения логики работы комбинационной схемы потребуется всего лишь перепрошивка ПЗУ, а не проектирование новой схемы из логических элементов. Задержка ПЗУ при замене комбинационной схемы любой сложности остается одной и той же, она равна задержке выборки адреса микросхемы ПЗУ. При сложной заменяемой комбинационной схеме ПЗУ может оказаться даже быстрее.

Однако использование ПЗУ для замены комбинационных схем имеет и довольно серьезные недостатки. Дело в том, что микросхемы ПЗУ еще больше, чем комбинационные микросхемы, чувствительны к моменту изменения входных сигналов (адресных разрядов). На выходах данных микросхем ПЗУ при любом изменении входного кода адреса могут появляться короткие паразитные импульсы. Поэтому лучше всего использовать ПЗУ для замены таких комбинационных схем, которые работают в статическом режиме и в которых короткие импульсы не имеют значения.

Рис. 11.7. Методы синхронизации выходных сигналов ПЗУ с помощью сигнала CS (а) и выходного регистра (б)

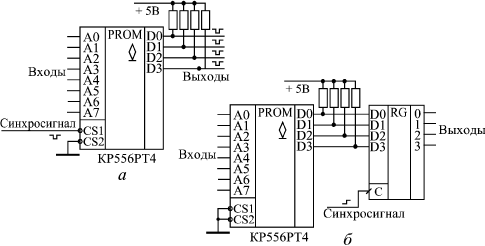
Можно также применять методы синхронизации выходных сигналов ПЗУ (рис. 11.7) с помощью управляющих сигналов выбора микросхемы CS (а) или же с помощью выходных триггеров и регистров (б). Суть синхронизации состоит в том, что выходные сигналы ПЗУ надо разрешать или фиксировать с помощью синхросигнала только тогда, когда все переходные процессы внутри микросхемы, вызванные сменой кода адреса, уже закончились и паразитные импульсы на выходах гарантированно отсутствуют.

Микросхемы ПЗУ могут заменять собой любые комбинационные микросхемы: дешифраторы, шифраторы, компараторы кодов, сумматоры, мультиплексоры, преобразователи кодов и т.д. Однако при подобной замене всегда стоит подумать, не лучше ли использовать уже готовые микросхемы, чем изготавливать новые (программировать ПЗУ). Микросхемы ПЗУ могут оказаться медленнее стандартных комбинационных микросхем и потреблять больший ток питания. К тому же они могут требовать выходных резисторов, если микросхемы имеют выходы ОК или при использовании входов CS у микросхем с выходами 3С. Другое дело, когда ПЗУ выполняет функцию, отличающуюся от функции стандартной комбинационной микросхемы. Простейший пример — дешифратор с положительными, а не с отрицательными (как в стандартных сериях) активными выходными сигналами.

В общем случае ПЗУ можно рассматривать как преобразователь входного кода (кода адреса) в выходной код (код данных) по произвольному закону, задаваемому разработчиком. Это позволяет не только преобразовывать друг в друга различные стандартные коды, но и выполнять множество других функций, например, использовать ПЗУ как простейший табличный вычислитель. Для этого нужно на адресные разряды ПЗУ подать код входного числа (аргумента), а на выходах разрядов данных получить код выходного числа (функции). Такой табличный вычислитель имеет очень высокое быстродействие по сравнению с другими типами вычислителей (время вычисления функции равно задержке выборки адреса ПЗУ).

В качестве простейшего примера рассмотрим вычислитель для возведения в квадрат 4-разрядного двоичного числа (рис. 11.8). Вычислитель выполнен на микросхеме ПЗУ типа РЕ3, у которого использованы четыре разряда адреса и восемь разрядов данных. Он позволяет получать двоичные коды квадратов любых чисел в диапазоне от 0 (или в двоичном коде 0000, в 16-ричном коде 0) до 15 (или в двоичном коде 1111, в 16-ричном коде F), которые принимают значения от 0 (или в двоичном коде 00000000, в 16-ричном — 00) до 225 (или в двоичном коде 11100001, в 16-ричном — E1).

Рис. 11.8. Вычислитель квадратов входных чисел

Карта прошивки ПЗУ вычислителя квадратов (табл. 11.3) будет очень проста: код данных в каждой ячейке равен квадрату кода адреса этой ячейки. Используется всего 16 ячеек памяти, содержимое остальных 16 ячеек не имеет значения (что обозначено в таблице ХХ).

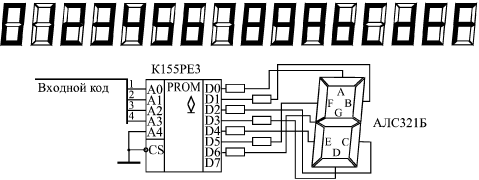
На такой же точно схеме (рис. 11.8) можно сделать и вычислитель квадратов в двоично-десятичном коде. В этом случае будет использовано всего лишь десять ячеек памяти с адресами от 0 до 9, а в ячейках будут записаны их квадраты от 0 до 81.

Недостаток любого табличного вычислителя на ПЗУ — это необходимость увеличения вдвое требуемого объема памяти при увеличении разрядности входного числа на единицу. Например, при 8-разрядных входных числах требуется ПЗУ с количеством ячеек 256, при 16-разрядных входных числах — ПЗУ с количеством ячеек 64К, а при 32-разрядных входных числах — ПЗУ с количеством ячеек 4Г. Такие большие объемы очень трудно реализовать на серийно выпускаемых микросхемах. Поэтому табличные вычислители на ПЗУ обычно строятся только для разрядности входных чисел не более 16.

Одно из наиболее распространенных применений ПЗУ как преобразователя кодов — это построение на их основе всевозможных индикаторов, отображающих на экране буквы и цифры. ПЗУ в данном случае переводит код (номер) буквы или цифры в ее изображение. Конечно, в данном случае заменить ПЗУ комбинационной схемой совершенно невозможно, так как букв и цифр очень много, а их изображения очень разнообразны.

Простейший пример данного применения ПЗУ — это управление знаковым семисегментным индикатором, знакомым всем по калькуляторам, кассовым аппаратам, электронным часам, весам и т.д. В семисегментных индикаторах изображение всех цифр от 0 до 9 строится всего из семи сегментов (отрезков линий) (рис. 11.9).

Рис. 11.9. Дешифратор знакового семисегментного индикатора на ПЗУ

Чтобы отобразить в виде цифры 4-разрядный двоичный код, надо этот код преобразовать в 7-разрядный код, каждому разряду которого будет соответствовать один сегмент индикатора. То есть коду 0000 должно соответствовать изображение нуля (6 сегментов, расположенных по периметру), а коду 0001 — изображение единицы (два правых вертикальных сегмента). Для повышения универсальности индикатора удобно дополнить десять цифр еще и шестью буквами, использующимися в 16-ричном коде (A, B, C, D, E, F). Семь сегментов индикатора позволяют сделать и это, правда, изображения букв получаются не слишком качественными.

ПЗУ типа РЕ3, используемое в качестве дешифратора индикатора, имеет 4 входа и 7 выходов (старший разряд адреса и старший разряд данных не используются). Карта прошивки ПЗУ приведена в табл. 11.4. Нулевой сигнал на каждом из выходов данных ПЗУ зажигает соответствующий ему сегмент.

ПЗУ позволяют также формировать и более сложные изображения букв и цифр — матричные. Такие изображения используются, например, в табло типа "бегущая строка", на экранах мониторов, в больших рекламных табло. Каждая буква, цифра, другой знак располагается в данном случае на прямоугольной матрице, называемой знакоместом и состоящей из нескольких строк и нескольких столбцов точечных элементов изображения, которые могут зажигаться независимо друг от друга. Чем больше строк и столбцов в знакоместе, тем более качественное изображение букв и цифр можно получить. Минимально возможный размер знакоместа — 5 столбцов на 7 строк, то есть всего 35 элементов изображения.

ПЗУ в данном случае содержит в себе информацию об изображениях всех возможных букв и цифр (обычно этот набор включает в себя 256 символов). Но выходной код ПЗУ имеет мало разрядов, поэтому каждый такой код, соответствующий одному адресу, представляет собой информацию об изображении не целого символа, а только одной его строки (или столбца). Информация о целом символе занимает в ПЗУ столько ячеек, сколько в изображении символа имеется столбцов (или строк). Пример матричного знакогенератора на ПЗУ приведен на рис. 11.10.

Рис. 11.10. Матричный знакогенератор на ПЗУ

В данном случае используется знакоместная матрица из 8 строк и 8 столбцов. В каждую ячейку ПЗУ записывается код изображения одной из 8 строк одного из 256 символов. Изображение одного символа занимает 8 последовательно расположенных ячеек в ПЗУ. Для букв и цифр правый столбец знакоместа не используется, он служит для отделения знаков друг от друга, но для специальных символов (например, для графических) он может и использоваться. В случае матричного светодиодного индикатора перебор строк может осуществляться 3-разрядным счетчиком с дешифратором 3–8 на его выходе. В случае телевизионного монитора перебор строк осуществляется с помощью генератора вертикальной развертки изображения.

Составление карты прошивки такого ПЗУ непросто, оно обычно производится с помощью специальных программ на компьютере. Но принцип составления прост. Например, если активному (зажженному) элементу изображения соответствует единичный сигнал, то для нулевой строки символа "М", показанного на рисунке, в ПЗУ надо записать 10000010, для первой строки — код 11000110, для второй — код 10101010, для третьей — 10010010 и т.д.

Поиск по сайту: