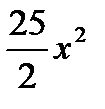|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Использование признака Даламбера при исследовании на сходимость рядов
По дисциплине «Элементы высшей математики» 1. В результате умножения матриц 1) 2 2) 18 3) 0 4) -2 1.1 Задана матрица 1)
1.2 Задана матрица 1)
3. Определитель 1) 6 2) -6 3) 8 4) 0 4. Переменная y системы уравнений 1)
5.1 Длина вектора 1) 6 2) 3) 20 4) 5.2 Даны векторы 1) (1; 16) 2) (5; 4) 3) (-5; -2) 4) (-1; 4)
6. Уравнение прямой, проходящей через две данные точки А(-1; 1) и В(7; 0), имеет вид… 1) 2) 3) 4)
7. Уравнение 1) эллипс 2) окружность 3) параболу 4) гиперболу
8.1 Сумма 1) 2) 3) 4)
8.2 Разность 1) 2) 3) 4)
8.3 Произведение 1) 2) 3) 4)
8.4 Частное 1) 2) 3) 4) Данному изображению точки А соответствует комплексное число
1) 2) 3) 4) 10. Корнем уравнения 1) 2) 3) -3 4) -1 11.1 Точка х = 1 для функции 1) Разрывом II рода 2) Разрывом I рода 3) Точкой непрерывности 4) Точкой устранимого разрыва
11.2 Точка х = 1 для функции 1) Разрывом II рода 2) Разрывом I рода 3) Точкой непрерывности 4) Точкой устранимого разрыва 12.1 Значение предела 1) 3 2) ¥ 3) 0 4) -3 12.2 Значение предела 1) ¥ 2) 0 3) 4) 3 13. Значение предела 1) - 2) 3) 0 4) ¥ 14. Значение предела 1) 2) 2 3) 0 4) 15. Производная функции 1) 2) 3) 4) 16.1 Точка перегиба графика функции 1) (0; -1) 2) (1; -3) 3) (-1; -5) 4) (2; -5) 16.2 График функции 1) 2) 3) 4) 16.3 График функции 1) 2) 3) 4) 17. Множество всех первообразных функции 1) 2) 3) 4) 18. В результате подстановки 1) 2) 3) 4)
19. Площадь фигуры, изображенной на рисунке, определяется интегралом:
1) 2) 3) 4) 20.1 Повторный интеграл 1) 2) 3) 4) 20.2 Повторный интеграл 1) 2) 3) 4)
21. Частная производная 1) 2) 3) 4) 22. Разделение переменных в дифференциальном уравнении 1) 2) 3) 4)
23. Общее решение дифференциального уравнения 1) 2) 3) 4)
24.1 Общее решение дифференциального уравнения
1) 2) 3) 4)
24.2 Если общее решение линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами имеет вид 1) 2) 3) 4) 25. Четвертый член числового ряда 1) 2) 3) 4)
26.1 Использование радикального признака Коши при исследовании на сходимость рядов А)
1) Ряды А и В сходятся 2) Ряд А сходится, ряд В расходится 3) Ряд А расходится, ряд В сходится 4) Ряды А и В расходятся
Использование признака Даламбера при исследовании на сходимость рядов А) 1) Ряды А и В сходятся 2) Ряды А и В расходятся 3) Ряд А сходится, ряд В расходится 4) Ряд А расходится, ряд В сходится 27.1 Для функции
1) 2) 3) 4)
27.2 Для функции
1) 2) 3) 4)
Поиск по сайту: |
 и
и 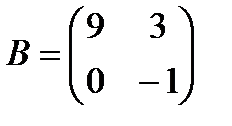 элемент а21 равен
элемент а21 равен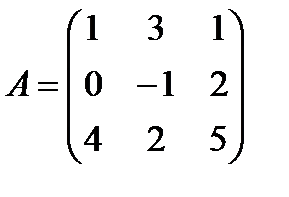 . Алгебраическое дополнение А11 вычисляется по формуле…
. Алгебраическое дополнение А11 вычисляется по формуле… 2)
2)  3)
3) 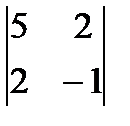 4)
4) 
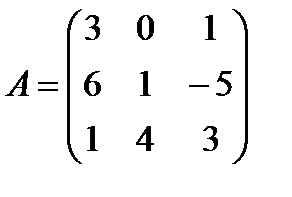 . Минор М12 вычисляется по формуле…
. Минор М12 вычисляется по формуле…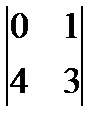 2)
2)  3)
3)  4)
4) 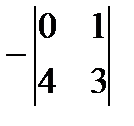
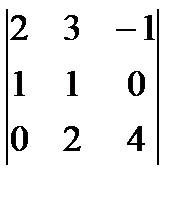 равен…
равен… определяется по формуле...
определяется по формуле...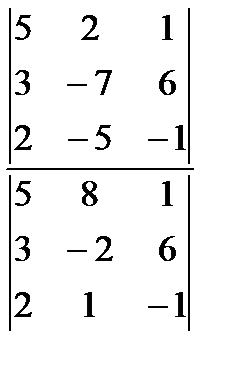 2)
2) 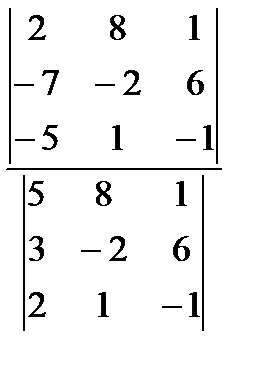 3)
3)  4)
4) 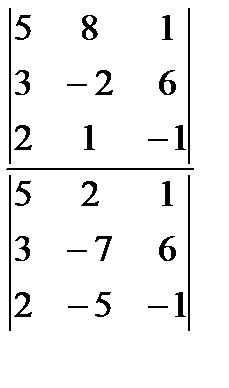
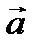 = (-2; 4) равна:
= (-2; 4) равна: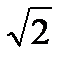
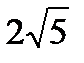
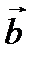 = (-3; 1). Тогда координаты вектора
= (-3; 1). Тогда координаты вектора 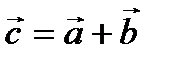 равны:
равны:
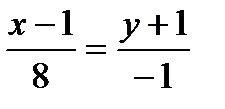


 задает на плоскости
задает на плоскости комплексных чисел
комплексных чисел  и
и 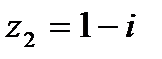 равна…
равна…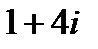
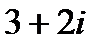
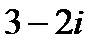

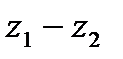 комплексных чисел
комплексных чисел 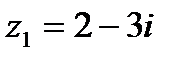 и
и 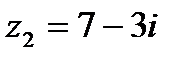 равна…
равна…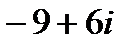



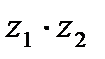 комплексных чисел
комплексных чисел 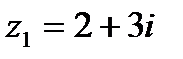 и
и  равно…
равно…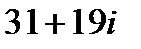
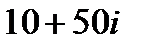
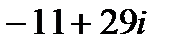

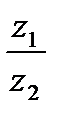 комплексных чисел
комплексных чисел 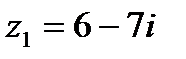 и
и 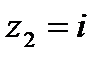 равно…
равно…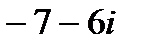
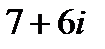
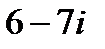
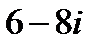
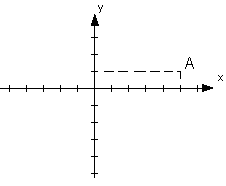

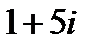

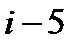
 является число…
является число…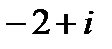
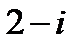
 является:
является: является:
является: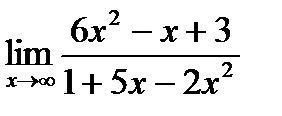 равно
равно равно
равно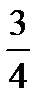
 равно
равно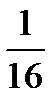
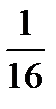
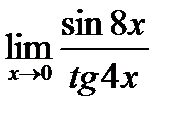 равно:
равно:

 имеет вид:
имеет вид: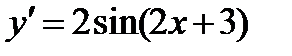


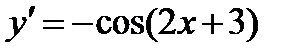
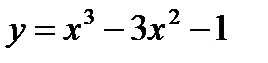 имеет координаты
имеет координаты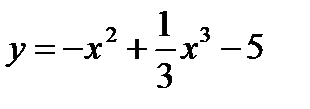 является выпуклым на промежутке
является выпуклым на промежутке
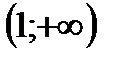
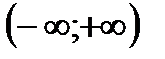

 является вогнутым на промежутке
является вогнутым на промежутке имеет вид:
имеет вид: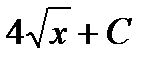
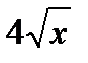
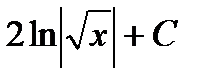
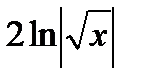
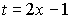 интеграл
интеграл  приводится к виду
приводится к виду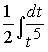

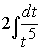




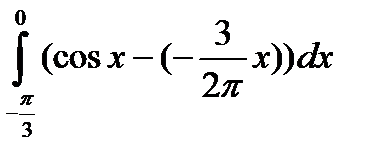

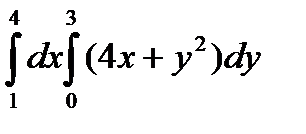 сводится к определенному интегралу:
сводится к определенному интегралу:

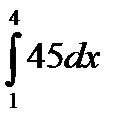

 сводится к определенному интегралу:
сводится к определенному интегралу: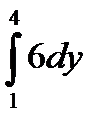

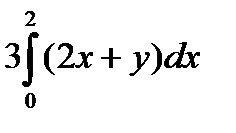

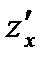 функции
функции 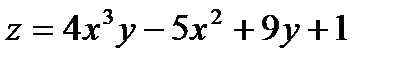 имеет вид:
имеет вид: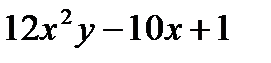
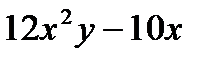


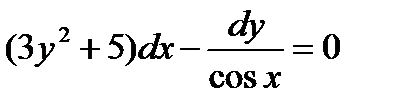 приведет его к виду:
приведет его к виду: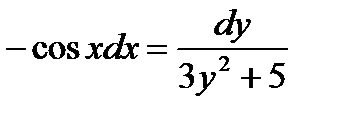

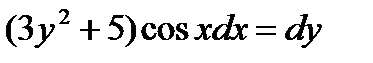
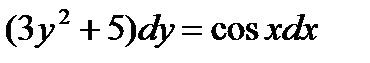
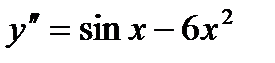 имеет вид:
имеет вид: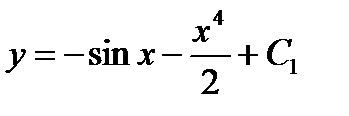

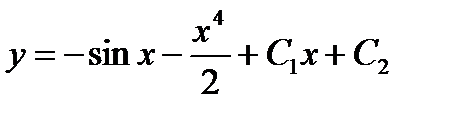
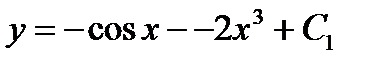
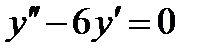 имеет вид:
имеет вид: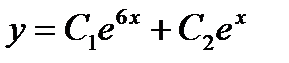
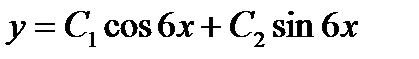
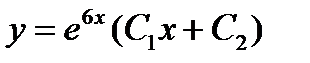
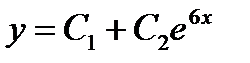
 , то корни характеристического уравнения равны:
, то корни характеристического уравнения равны: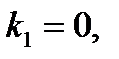
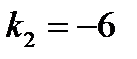
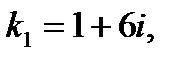
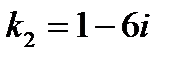
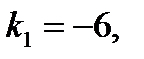
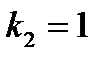

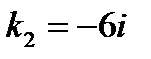
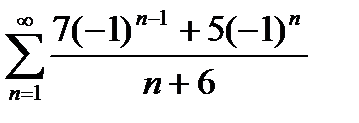 равен:
равен:
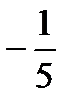
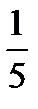

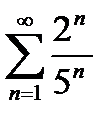 и В)
и В) 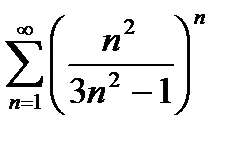 позволяет сделать вывод:
позволяет сделать вывод: и В)
и В)  позволяет сделать вывод:
позволяет сделать вывод: первый ненулевой член ряда Маклорена
первый ненулевой член ряда Маклорена имеет вид:
имеет вид: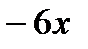
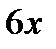
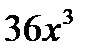

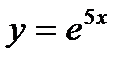 второй член ряда Маклорена
второй член ряда Маклорена