 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение систем линейных уравнений. ЛАБОРАТОРНАЯ РАБОТА №7
ЛАБОРАТОРНАЯ РАБОТА №7 Решение уравнений и систем уравнений в Matlab. 1. Решение уравнений вида Для простоты будем рассматривать случай, когда Для нахождения корней многочлена в Matlab используется функция roots. Полином задаётся в виде вектора коэффициентов при степенях
Решение систем линейных уравнений Система линейных алгебраических уравнений в самом общем случае имеет вид:
Для вычислений в Matlab удобно представлять такую систему в виде матрицы коэффициентов
Тогда систему (1) можно записать в виде:
где
Способ 1. Метод обратной матрицы. Если
Таким образом, нам необходимо посчитать обратную матрицу для матрицы коэффициентов и перемножить её со столбцом свободных членов.
Пример 2. Решение системы методом обратной матрицы A=[1 -2 1; 2 -5 -1; -7 0 1]; b=[2; -1; -2]; x=inv(A)*b % Решение системы x=A-1b
Способ 2. Метод Крамера. Суть метода Крамера состоит в следующем. Если для представления системы уравнений (1.1) соблюдается условие
и т. д., где
т. е. определитель матрицы А (1.1), в которой
Пример 3. Решение системы методом Крамера A = [1 2 3 4; -1 2 -3 4; 0 1 -1 1; 1 1 1 1]; b = [30;10;3;10]; % Проверим невырожденность системы rank(A) >> ans = 4 % По правилу Крамера по очереди заменяем столбцы исходной матрицы % столбцом свободных членов. Для этого создаём 4 копии матрицы – по % числу столбцов A1 = A; A2 = A; A3 = A; A4 = A; A1(:,1) = b; A2(:,2) = b; A3(:,3) = b; A4(:,4) = b; % вычисляем определители x1 = det(A1) / det(A); x2 = det(A2) / det(A); x3 = det(A3) / det(A); x4 = det(A4) / det(A); x=[x1;x2;x3;x4]; % Проверим решение A*x - b>> ans = 0 Способ 3. Метод Гаусса. Метод Гаусса предполагает проведение преобразований с так называемой расширенной матрицей системы уравнений, т. е. с матрицей вида В Matlab для решения систем уравнений методом Гаусса используется встроенная функция rref.
Пример 4. Решение системы уравнений методом Гаусса A = [1 2 3; 1 -3 2; 1 1 1]; b = [7;5;3]; % Формируем расширенную матрицу системы C = [A b]; % Приведём её к ступенчатому виду, выполнив прямой и обратный ход % метода Гаусса D = rref(C)>> D = 1 0 0 1 0 1 0 0 0 0 1 2 % Последний столбец матрицы есть решение x = D(:,4); % Проверим его A*x - b>> ans = 0
Поиск по сайту: |

 - полином, т. е. имеет вид
- полином, т. е. имеет вид  . Тогда, согласно следствию из основной теоремы алгебры, уравнение
. Тогда, согласно следствию из основной теоремы алгебры, уравнение  имеет ровно
имеет ровно  в общем случае комплексных корней.
в общем случае комплексных корней.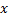 , т. е. имеет вид
, т. е. имеет вид  .
.
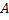 и вектора свободных членов
и вектора свободных членов 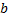 :
:

 – вектор-столбец неизвестных.
– вектор-столбец неизвестных.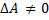 , то тогда система (1) имеет единственное решение, которое выражается как
, то тогда система (1) имеет единственное решение, которое выражается как
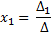

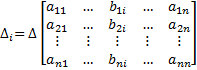
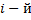 столбец заменён столбцом свободных членов
столбец заменён столбцом свободных членов  с целью приведения её к виду
с целью приведения её к виду 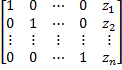 . Последний столбец будет содержать значения неизвестных. Система будет иметь единственное решение, когда
. Последний столбец будет содержать значения неизвестных. Система будет иметь единственное решение, когда 