 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Должен ли инженер уметь программировать?Стр 1 из 2Следующая ⇒
Лабораторная работа № 3. Разработка программ. Синтаксис файлов-функций, управляющие структуры MATLAB Должен ли инженер уметь программировать?
Вопрос этот закономерный. Индустрия программного обеспечения (software) предлагает для решения самых разнообразных задач уже готовые мощные программные комплексы. Это, например, рассматриваемый здесь MATLAB для математических вычислений, NASTRAN для задач строительной механики, CorelDraw для графических работ и так далее, и так далее. Так не лучше ли воспользоваться этими профессионально выполненными продуктами, а не заниматься кустарщиной. Практика, однако, показывает, что полностью предусмотреть все возможные потребности пользователя, несмотря на громкие рекламные заявления, производителям программного обеспечения пока не удается. Более того, часто подтверждается наблюдение Джадда Д.Р. [1]: «Программное обеспечение, рассчитанное на широкий круг пользователей, оказывается непригодным для конкретных применений». Поэтому в любом КБ, несмотря на оснащенность современными программными средствами, сотрудникам то и дело приходится составлять собственные программы. Простой пример. Предположим, вы получили задание выполнить расчет изгибных колебаний тонкостенной балки (лопасти вертолета, или крыла самолета, или еще чего-нибудь в этом роде). Необходимая программа в вашем отделе есть, но в качестве исходных данных для нее необходимо подготовить жесткостные и инерционные характеристики сечений балки:
Вообще-то эти характеристики можно рассчитать вручную, используя известные методики из учебников строительной механики. Однако такие ручные расчеты весьма трудоемки и имеют невысокую точность. Между тем даже для одной балки эти характеристики требуется получить хотя бы для 20-30 сечений. А ведь не исключено, что ваш начальник вскоре вновь поручит вам аналогичный расчет. Поэтому имеет прямой смысл потратить время на то, чтобы написать собственную небольшую программу расчета этих характеристик. Это позволит вам сэкономить много времени в будущем, избавит от утомительных расчетов и поднимет ваш авторитет в глазах коллег и начальства. В практике любого инженерного подразделения подобные задачи возникают регулярно. Кстати и в упомянутых ранее программных продуктах их создатели предоставляют возможность пользователю дополнить уже имеющиеся средства своими собственными программами. Например, в известной программе FEMAP этой цели служит встроенный язык программирования FEMAP Basic Scripting Language. Что касается MATLAB’а, то он оснащен мощным языком программирования, с которым вы ненавязчиво знакомитесь с первой страницы этого пособия (команды, файлы-сценарии, операции с массивами и т.д.). Итак, надеемся, что мы сумели доказать, что инженер обязан уметь программировать. Впрочем, если наши аргументы вас не убедили, приведем еще один. Без зачета по вычислительной практике к экзаменам вы допущены не будете. К сожалению, авторы должны заметить, что хотя студенты вроде бы начинают изучать программирование с первого курса, умение программировать у большинства практически отсутствует. Как правило, знания, в лучшем случае, распространяются на синтаксис языка программирования, основные операторы и встроенные функции. Но вот как из этих кирпичиков сложить действующую программу для решения конкретной задачи, большинство студентов не знает. Между тем уже давно программирование не считается уделом избранных. Если еще 40-50 лет назад считалось, что программировать, как писать стихи, дано не каждому, то уже с 70-х годов XX века программирование из разряда искусств перешло в разряд ремесел. То есть имеются определенные приемы и правила, следуя которым любой человек может написать действующую программу для решения достаточно сложных задач. Обучение этому ремеслу и является целью настоящей главы. Основной акцент будет сделан именно на методике построения программ. Подробного перечня зарезервированных слов, используемых символов, синтаксических правил здесь не приводится. Для этого существуют справочники и HELP. Тем не менее, хотя основные программные конструкции: подпрограммы, операторы цикла, условные операторы и т.п. сходны во всех языках программирования, они все-таки имеют и некоторые различия. Поэтому прежде чем перейти к технологии, коротко ознакомимся с основными инструментами: подпрограммами MATLAB’а – М‑функциями и управляющими структурами – if, for, while, switch.
М-файл – функция
Ранее вы уже встречались с программированием в MATLAB’е, когда познакомились с М-файлами – сценариями (script files). Используя только файлы-сценарии, можно решать достаточно сложные задачи. Однако, у файлов-сценариев имеются и существенные недостатки.
% Script: длина гипотенузы x = a^2 + b^2; c = sqrt(x) Сохраним этот файл под именем hyposcr.m (сокращение слов hypotenuse и script). Теперь посмотрим, как будет выглядеть фрагмент сеанса, если нам потребуется рассмотреть несколько треугольников:
>> a=3; >> b=4; >> hyposcr c = >> a=6; >> b=3; >> hyposcr c = 6.7082 >> a=5.3; >> b=2.1; >> hyposcr c = 5.7009
Уже здесь бросается в глаза надоедливая обязанность: перед каждым вызовом сценария надо вручную присваивать новые значения переменным Гораздо более удобно использование другой разновидности М-файлов: файлов-функций. Создайте в редакторе следующий файл:
% Function: длина гипотенузы function c = hypofun(a,b) x = a^2 + b^2; c = sqrt(x);
Сохраните его под именем hypofun.m. С использованием этого файла-функции рассмотренный ранее фрагмент будет выглядеть гораздо компактней.
>> c1 = hypofun(3,4); >> c2 = hypofun(6,3); >> c3 = hypofun(5.3,2.1); Внешне файл-функция отличается от файла-сценария только одной строчкой ‑ первой. Она начинается с ключевого слова function. Далее следует имя переменной, в которую надо будет поместить результат вычислений. После знака = следует идентификатор, который придумывает автор функции (в данном случае – мы с вами). Это имя функции. Обратите внимание, что это же имя мы использовали для файла, в котором сохранили эту функцию. После имени функции в круглых скобках список входных параметров – аргументов функции. Вызов функции, созданной нами, осуществляется так же, как и вызов стандартных функций MATLAB’а – мы записываем имя функции, и в скобках задаем значения аргументов. На этом примере уже можно отметить первое преимущество функций перед сценариями: здесь гораздо удобнее организована передача аргументов и возврат результата вычислений.
С использованием функции
>> x=2; >> a=4; >> b=3; >> AD = hypofun(a,b) + x AD = 7
С использованием сценария
>> x=2; >> a=4; >> b=3; >> hyposcr; c = >> AD = c + x AD = 30 Здесь мы видим, что использование сценария оказалось не просто менее удобным, но и вообще привело к неправильному результату. Хотя на самом деле виноват в этом не файл-сценарий, а неправильное его использование, полезно разобраться в причинах появления этой ошибки.
Сначала, пока мы присваиваем переменным Далее выделяются ячейки под внутренние переменные функции. В нашей функции такая переменная только одна ‑ Наконец, после того как функция будет выполнена и переменной-результату >> AD = hypofun(a,b) + x После этого ячейки памяти, отведенные под локальные переменные функции, освобождаются. Локализация переменных является важным средством, защищающих нас от многих возможных ошибок. Благодаря ей вы можете, один раз написав нужную вам функцию, свободно использовать ее и в командном окне, и в других функциях, не опасаясь за содержимое важных переменных. Замечание. Такой способ передачи параметров называется передачей по значению. Существует и другой способ, называемый передачей по ссылке. В этом случае функция будет работать не с копией аргумента, а с самим аргументом. Такой способ бывает очень полезен, например, при работе с большими матрицами. Однако при этом увеличивается опасность ошибок. Поэтому, пока вы не стали опытными программистами, передачу по ссылке лучше не использовать.
Возможно, вам потребуется, чтобы ваша функция возвращала не один результат, а несколько. Например, в рассмотренном выше примере, кроме гипотенузы вам нужна еще и площадь треугольника. В этом случае нашу функцию следует изменить следующим образом:
% Function: Гипотенуза и площадь прямоугольного треугольника function [c,S] = hypoarea(a,b) x = a^2 + b^2; c = sqrt(x); S = a*b;
Отличие в этом случае заключается лишь в том, что список результатов (выходных параметров) заключается в квадратные скобки. Аналогично изменяется и вызов такой функции:
>> [g,S]=hypoarea(3,4) g = S =
В заключение параграфа о том, когда и зачем следует использовать М-функции. 1. Первое напрашивающееся и очень полезное применение. Если в ходе решения какой-то задачи вам очень часто приходится набирать одно и то же выражение, например cos(x)^2*sin(x) – sinh(2*x) имеет смысл создать функцию с каким-нибудь запоминающимся именем вроде c2sh() и использовать ее далее, экономя время и снижая вероятность ошибки при наборе с клавиатуры. 2. Второе и главное применение – создание приложений. Приложения (Applications) – это программы, которые полностью решают некоторую прикладную задачу. Примеры приложений – Блокнот, для работы с небольшими текстовыми файлами, Калькулятор, для выполнения арифметических вычислений. К приложениям, но неизмеримо более сложным, можно отнести такие системы, как MathCad и MATLAB. Даже самые простые приложения представляют собой взаимодействующую совокупность не одной, а, по крайней мере, нескольких функций.
Поиск по сайту: |
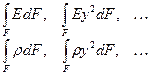
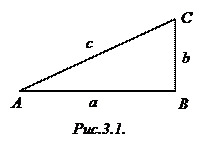 Рассмотрим вновь учебный пример из первого занятия: вычисление гипотенузы прямоугольного треугольника
Рассмотрим вновь учебный пример из первого занятия: вычисление гипотенузы прямоугольного треугольника  (рис.3.1). Для решения этой задачи можно использовать такой script-файл:
(рис.3.1). Для решения этой задачи можно использовать такой script-файл: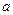 и
и  . Есть и еще одна неприятность. Если вам сейчас потребуется гипотенуза первого треугольника, то, оказывается, что в переменной
. Есть и еще одна неприятность. Если вам сейчас потребуется гипотенуза первого треугольника, то, оказывается, что в переменной 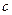 этого значения уже нет. Все придется повторять заново.
этого значения уже нет. Все придется повторять заново. Механизм передачи данных имеет и более серьезные преимущества, чем простое удобство. Рассмотрим для иллюстрации следующую простую задачу (рис. 3.2): Требуется определить длину AD при заданных
Механизм передачи данных имеет и более серьезные преимущества, чем простое удобство. Рассмотрим для иллюстрации следующую простую задачу (рис. 3.2): Требуется определить длину AD при заданных  . Такие задачи вам приходилось решать на уроках физики в восьмом классе (определить перемещение точки при движении по заданной траектории). Попробуем решить эту задачу, сначала используя файл-функцию, а затем файл-сценарий:
. Такие задачи вам приходилось решать на уроках физики в восьмом классе (определить перемещение точки при движении по заданной траектории). Попробуем решить эту задачу, сначала используя файл-функцию, а затем файл-сценарий: Оперативную память компьютера можно упрощенно представить в виде длинного ряда ячеек, в каждой из которых может храниться число. При использовании файла-сценария распределение памяти изображено на рис 3.3. При использовании сценария сначала последовательно выделяются ячейки памяти и в них заносятся значения переменных
Оперативную память компьютера можно упрощенно представить в виде длинного ряда ячеек, в каждой из которых может храниться число. При использовании файла-сценария распределение памяти изображено на рис 3.3. При использовании сценария сначала последовательно выделяются ячейки памяти и в них заносятся значения переменных 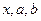 . Затем следует вызов сценария. Напомним, что сценарий выполняется построчно так, как если бы вы набирали его строки с клавиатуры. Первая же строка сценария (посмотрите на предыдущую страницу) проясняет причину ошибки. Оказывается, что мы использовали переменную
. Затем следует вызов сценария. Напомним, что сценарий выполняется построчно так, как если бы вы набирали его строки с клавиатуры. Первая же строка сценария (посмотрите на предыдущую страницу) проясняет причину ошибки. Оказывается, что мы использовали переменную 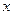 для того, чтобы поместить в нее сумму квадратов катетов. А нужное нам значение (x=2) оказалось испорченным.
для того, чтобы поместить в нее сумму квадратов катетов. А нужное нам значение (x=2) оказалось испорченным.