 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Представление данных матрицами
Матрицей размерности Если матрица имеет размер Если матрица имеет размер Если матрица имеет размер В MATLAB все числовые данные представляются в виде матриц. Поэтому любое число рассматривается как матрица размера Рассмотрим самый простой задания матриц в MATLAB. Для задания вектора-строки (т.е. матрицы размера >> B=[1 3 -1] B = 1 3 -1 >> B=[1, 3, -1] B = 1 3 -1 Для задания вектора-столбца (т.е. матрицы размера >> C=[-1;2.1] C = -1.0000 2.1000 Комбинируя оба варианта разделителя, можно задать матрицу, число строк и столбцов которой больше одного (двумерный массив): >> A=[1 2 3 4;0 1 3 2] A = 1 2 3 4 0 1 3 2 Любое число рассматривается в MATLAB как матрица размера >> n=3 n = >> m=[3] m = >> whos A B C n m Name Size Bytes Class Attributes A 2x4 64 double B 1x3 24 double C 2x1 16 double m 1x1 8 double n 1x1 8 double Для доступа к отдельным элементам матриц указываются их индексы. Например, A(1,3) – элемент матрицы А, стоящий в 1-й строке и 3-м столбце; В(2) (В(1,2)) – второй элемент вектора-строки В. Далее мы будем часто использовать векторы-строки, элементы которых образуют арифметическую прогрессию. Они задаются следующим образом: >> v=1:2:7 v = 1 3 5 7 Элементами матриц могут быть любые выражения, допустимые в MATLAB. >> S=[-1+2*3 sqrt(2) abs(-3)] S = 5.0000 1.4142 3.0000 Упражнение 4. 1) Задать какую-нибудь матрицу R размерностью 2) Заменить значения элемента R(2,3) на противоположный (R(2,3)=–R(2,3)), вывести обновленную матрицу R в командное окно. Уменьшить на 4 элемент, стоящий в первой строке и третьем столбце, вывести обновленную матрицу R в командное окно. Удвоить все элементы второго столбца (>> R(:,2)=2*R(:,2)). Утроить все элементы первой строки, вывести обновленную матрицу R в командное окно. 3) Задать векторы-строки размерности 4) Задать вектор-строку с элементами от -2 до 10 с шагом 2, утроить все ее элементы. 5) Задать вектор-строку с элементами от 45 до 5 с шагом -5, определить ее размерность.
Поиск по сайту: |
 называется прямоугольная таблица, состоящая из n строк и m столбцов. Традиционно в математике эту таблицу заключают в круглые скобки. Например,
называется прямоугольная таблица, состоящая из n строк и m столбцов. Традиционно в математике эту таблицу заключают в круглые скобки. Например, 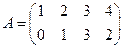 - матрица размерности
- матрица размерности  ;
; , т.е. состоит только из одной строки, то ее называют вектором-строкой. Например,
, т.е. состоит только из одной строки, то ее называют вектором-строкой. Например,  - матрица размерности
- матрица размерности 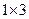 , т.е. вектор-строка.
, т.е. вектор-строка. , т.е. состоит только из одного столбца, то ее называют вектором-столбцом. Например,
, т.е. состоит только из одного столбца, то ее называют вектором-столбцом. Например,  - матрица размерности
- матрица размерности 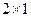 , т.е. вектор-столбец.
, т.е. вектор-столбец. , т.е. состоит из одного столбца и одной строки, то ее называют скаляром. Например,
, т.е. состоит из одного столбца и одной строки, то ее называют скаляром. Например,  - матрица размерности
- матрица размерности 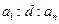 :
: .
. и
и  , задать 3 вектора-столбца разной размерности.
, задать 3 вектора-столбца разной размерности.