Разработка аналитических моделей

ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ

ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С ПРИМЕНЕНИЕМ

ИНСТРУМЕНТАЛЬНЫХ ПАКЕТОВ СИСТЕМЫ MATLAB

Цель работы: освоение вариационных методов решения задач оптимального управления с помощью точных и приближенных аналитических моделей, а также с использованием средств символьной обработки математической системы MATLAB и имитационного моделирования инструментального пакета Simulink.

Постановка задач исследования

В данной лабораторной работе рассматриваются задачи оптимального управления, решаемые классическими вариационными методами. Для предлагаемых функционалов требуется построить точные и приближенные аналитические модели нахождения экстремалей этих функционалов, а также точные и приближенные значения их экстремумов. Используя средства символьной обработки математической системы MATLAB, необходимо разработать программную модель для решения указанных задач. С помощью инструментального пакета Simulink построить имитационные модели нахождения экстремалей и значений функционалов, произвести верификацию всех разработанных моделей и оценку влияния помех на качество управления.

Разработка аналитических моделей

Формализация многих задач оптимального управления приводит к интегральным функционалам классического вариационного исчисления, отображающих функцию или набор функций в число. Решение задачи в этом случае заключается в нахождении таких функций, которые обеспечивают минимальное или максимальное значение соответствующего функционала. Эти функции называются экстремалями задачи. В вариационном исчислении доказывается, что экстремали должны удовлетворять некоторым дифференциальным уравнениям. Однако удовлетворение этим уравнениям представляет собой лишь необходимое условие экстремума функционала. Поэтому, решив дифференциальные уравнения и найдя экстремали, необходимо тем или иным способом определить, что они обеспечивают экстремум рассматриваемого функционала.

В зависимости от вида функционала необходимые условия записываются следующим образом:

а) для функционала

:

(1)

где F_y – частная производная по y от функции F;

F_y¢ – частная производная по y′ от той же функции F (это условие называется уравнением Эйлера);

б) для функционала

:

		(2)
		(3)

где F_z и F_z¢– соответствующие частные производные;

в) для функционала

:

		(4)
		(5)

г) для функционала

:

		(6)
		(7)

д) для функционала

:

(8)

где u_x и u_y – частные производные от искомой функции u(x, y) соответственно по x и y.

F_u, F_ux, F_uy – частные производные от подынтегрального выражения;

u_l(x, y)– граничные условия, т.е. значения функции u(x, y) на контуре области интегрирования B (это дифференциальное уравнение называется уравнением Остроградского);

е) для функционала

:

(9)

где u_s(x, y, z)– значения функции u(x, y, z) на поверхности S объема интегрирования V;

ж) если в выражение функционала J[u(x, y, z)] входят производные функции u(x, y, z) до порядка n, то уравнение Остроградского имеет вид:

(10)

В табл. 1 приведено несколько примеров вариационных задач.

Таблица 1

Варианты задач для функционала типа J[y(x)]

№ п/п	Вид функционала	Функционал	Граничные условия
			y(0) = 0; y(1) = 0
			y(0) = 0; y(1) = 0
			y(0) = 0; y(2) = 0
			y(0) = 0; y(2) = 0
			y(-1) = 1; y(1) = 2

Нахождение экстремалей позволяет вычислять относительные, или локальные экстремумы. Математическое определение понятия локального экстремума интегрального функционала производится с помощью ε- окрестностей функций и их классов. Например, для простейшего функционала

,

(11)

в котором F является непрерывной функцией всех трех аргументов вместе с ее производными до второго порядка в некоторой области B плоскости (x, y) и при любых значениях y′, экстремаль ищется в классе функций C₁, имеющих в промежутке [x₀, x₁]непрерывную производную. В этом классе определяется ε-окрестность кривой y = y(x) как множество кривых y_i(x), которые во всем промежутке [x₀, x₁]удовлетворяют неравенству |y_i(x) − y(x)| ≤ ε. Иногда, кроме этого неравенства, добавляют еще одно: |y_i′(x) − y′(x)| ≤ ε. В первом случае говорят об ε-близости нулевого порядка, а во втором случае, при наличии двух неравенств, говорят об ε-близости первого порядка. Если окажется, что величина этого функционала для y(x), лежащей внутри упомянутой области B, принадлежащей классу C₁и удовлетворяющей предельным условиям:

не меньше (или не больше) его величины для любых других кривых класса C₁, находящихся в некоторой ε-близости к y(x) и удовлетворяющих тем же предельным условиям, то говорят, что функционал J[y(x)] достигает локального экстремума для кривой y(x).

Наряду с понятием локального экстремума вводится понятие абсолютного экстремума для некоторого класса функций D, для которых интеграл J[y(x)] имеет смысл. Говорят, что функционал J[y(x)] достигает в классе D абсолютного экстремума для кривой y(x), если величина этого функционала для y(x) не меньше (или не больше) его величины для всех других кривых класса D.

Для функционала аналогом дифференциала функции является его вариация ∂J, т.е. изменение функционала при замене функции из рассматриваемого класса на ε-близкую функцию из того же класса. Так, для функционала (11) вблизи экстремали y(x) его первая вариация записывается следующим образом:

(13)

где δy =αη(x), так что ε-близкая к y(x) функция будет y(x) +αη(x);

α – малый численный параметр;

η(x) – произвольная функция класса C₂, принимающая нулевые значения на концах промежутка интегрирования.

В качестве примера найдем точное и приближенное решение задачи о минимуме функционала

.

(14)

Построим графики функций y(x), y₀(x)и y₁(x), а также вычислим v[y(x)], v[y₀(x)]и v[y₁(x)], где y(x)– точное решение задачи.

Сначала найдем точное решение задачи. Функция y(x)должна удовлетворять уравнению Эйлера

.

(15)

В нашем случае

.

(16)

Тогда уравнение Эйлера будет иметь вид

.

(17)

Это линейное неоднородное уравнение. Его общее решение состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение имеет вид

.

(18)

Характеристическое уравнение r² − 1 = 0 имеет корни r₁= 1, r₂= −1. Общее решение однородного уравнения будет таким:

.

(19)

Частное решение неоднородного уравнения будем искать в виде y₂ = Ax. Подставляя это значение в неоднородное уравнение, получим: −Αx = 6x.Тогда Α = −6, y₂ = −6x.

Таким образом, общее решение неоднородного уравнения принимает вид:

.

(20)

Используя краевые условия, получим следующую систему уравнений для определения C₁и C₂.

.

(21)

Решая полученную систему, находим

Тогда

.

(22)

Учитывая, что

(23)

получим

.

(24)

В таком случае

.

(25)

С помощью MATLAB находим

.

(26)

Теперь найдем первое приближение точного решения. Его будем искать в виде

.

(27)

Тогда

.

(28)

В таком случае

.

(29)

Чтобы найти минимум j(a₀)возьмем производную и приравняем ее к нулю. Производную возьмем под знаком интеграла. Имеем

.

(30)

После преобразований получим

.

(31)

Взяв интеграл и приравняв его нулю, получим

.

(32)

Отсюда находим

Тогда

	.	(33)
	.	(34)

Теперь найдем второе приближение точного решения. Будем его искать в виде

.

(35)

Раскроем скобки и приведем подобные члены

.

(36)

Тогда

.

(37)

Функционал будет иметь вид

(38)

Чтобы найти минимум j(a₀, a₁), возьмем частные производные по a₀ и a₁и приравняем их к нулю. Решая полученную систему, определим a₀ и a₁:

.

Взяв интеграл и выполнив некоторые преобразования, получим первое уравнение

(39)

Аналогично

После преобразований получим второе уравнение

(40)

Решая систему уравнений, находим

Тогда второе приближение будет таким

.

(41)

В таком случае

.

(42)

Значение функционала

.

(43)

В нашем случае

.

что подтверждает правильность решения задачи.

Ниже приведено решение задачи с помощью MATLAB, построены графики функций y(x), y₀(x), y₁(x), а также графики функций
z₁(x) = y(x) – y₀(x), z₂(x) = y(x) – y₁(x).

Поиск по сайту: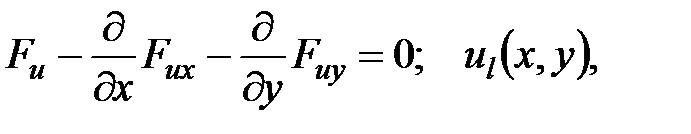
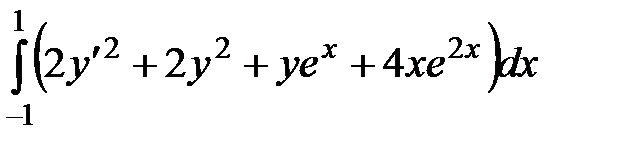
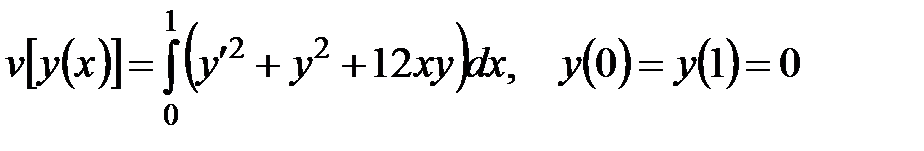
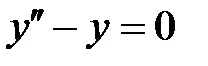
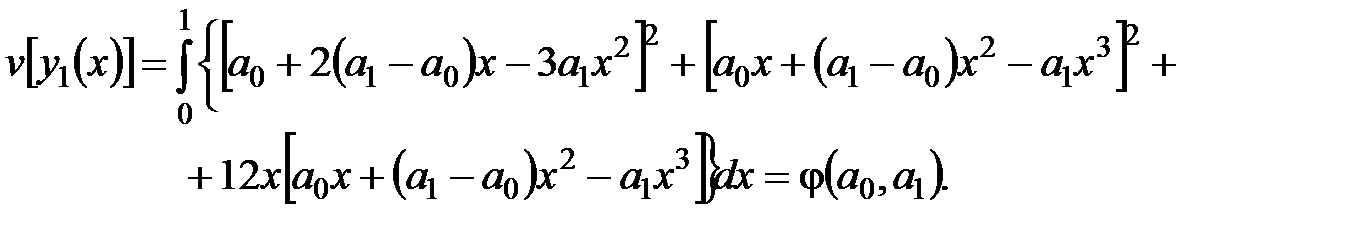
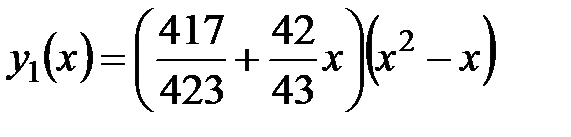
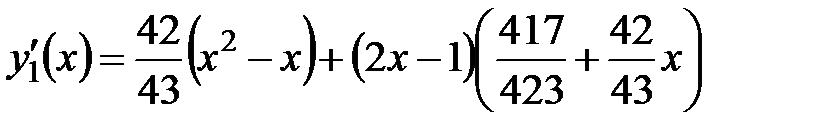