 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Диференціальне рівняння обертального руху твердого тіла навколо нерухомої осі
ДИНАМІКА ТВЕРДОГО ТІЛА В ЗАЛЕЖНОСТІ ВІД ТИПУ ЙОГО РУХУ
Диференціальні рівняння поступального руху твердого тіла Для розв’язування задач динаміки необхідно вміти складати диференціальні рівняння в залежності від виду руху твердого тіла. Основою для отримання таких рівнянь є загальні теореми динаміки механічної системи. При поступальному русі твердого тіла всі його точки (включаючи центр мас) мають геометрично рівні швидкості та прискорення. Отже, використовуючи теорему про рух центра мас, можемо записати:
Проектуючи векторне рівняння (9.1) на декартові координатні осі, маємо:
Рівняння (9.2) єдиференціальними рівняннями поступального руху твердого тіла. За їх допомогою можна розв’язувати дві основні задачі щодо поступального руху твердого тіла: 1. За заданим законом руху твердого тіла певної маси визначати головний вектор всіх зовнішніх сил, які діють на точки цього тіла 2. За заданими зовнішніми силами і початковими умовами визначити рівняння руху твердого тіла певної маси.
Диференціальне рівняння обертального руху твердого тіла навколо нерухомої осі Розглянемо обертання твердого тіла навколо нерухомої осі під дією зовнішніх сил Запишемо теорему про зміну кінетичного моменту механічної системи в проекціях на вісь
Характеристикою інертності тіла при обертальному русі є момент інерції тіла відносно осі обертання Перетворимо ліву частину рівняння (9.3), враховуючи, що
Тоді рівняння (9.3) матиме такий вигляд:
або
Рівняння (9.4) єдиференціальним рівнянням обертального руху тіла навколо нерухомої осі,що дозволяє розв’язувати такі задачі:
1. За заданим законом обертання тіла 2. За заданими зовнішніми силами, моментом інерції тіла і початковими умовами обертання визначати закон обертального руху тіла. 3. За заданими зовнішніми силами і кутовим прискоренням тіла
Поиск по сайту: |
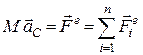 , де
, де  . (9.1)
. (9.1) ,
,  ,
, 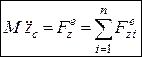 . (9.2)
. (9.2)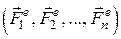 (рис. 9.1). Застосуємо принцип звільнення від в’язей.
(рис. 9.1). Застосуємо принцип звільнення від в’язей. :
: . (9.3)
. (9.3) Якщо розглядати обертання тіла за відсутністю сил тертя, то сума моментів реакцій в’язей відносно осі
Якщо розглядати обертання тіла за відсутністю сил тертя, то сума моментів реакцій в’язей відносно осі  .
. :
: .
. , (9.4)
, (9.4) . (9.4.а)
. (9.4.а) і його моментом інерції
і його моментом інерції  , що діють на тверде тіло.
, що діють на тверде тіло. визначити момент інерції
визначити момент інерції