 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приклади оформлення задач до розділу
Самостійна робота №2 Тема: Розв’язування задач з теми «Операції над випадковими подіями». Мета: Закріпити набуті знання та навички, перевірити їх при виконанні практичних завдань. Завдання 1. Засвоїти теоретичний матеріал згідно теми; 2. Дати відповіді на поставлені питання (лекція 2); 3. Виконати письмово приведені завдання; 4. Випишіть питання, що виникли в ході засвоєння матеріалу; 5. Зробіть висновки. Рекомендована література: 1. Барковський В.В. Теорія ймовірностей та математична статистика – К: Центр учбової літератури, 2010р. 2. Кочетков Е.С. Теорія ймовірностей і математична статистика – М: Форум, 2011р
Теоретичний матеріал Випадкові події та операції над ними. Забезпечення певного комплексу умов називають випробуванням або дослідом, а можливий результат випробування — подією. Наприклад, підкидання монети є випробуванням, а випадання «герба» або «номіналу» — подіями. Події позначатимемо великими латинськими літерами: А, В, C. Подію називають випадковою, якщо вона може відбутися або не відбутися в даному випробуванні. Достовірною називають подію, яка обов'язково відбудеться в даному випробуванні. Неможливою називають подію, яка точно не відбудеться в даному випробуванні. Зауважимо, що будь-яка подія пов'язана з певним випробуванням. Дві події називають сумісними, якщо поява однієї з них не виключає появи іншої в одному й тому самому випробуванні. Дві події називають несумісними, якщо вони не можуть відбутися одночасно в одному й тому самому випробуванні. Попарно несумісні випадкові події А1,А2,...,Ап утворюють повну групу подій, якщо внаслідок випробування одна з них обов'язково відбудеться. Наприклад, події «виграш», «програш» і «нічия» (для певного гравця) утворюють повну групу подій у випробуванні — грі в шахи двох суперників. Елементарними подіями (наслідками) у певному випробуванні називають усі можливі результати цього випробування, які не можна розкласти на простіші. Множину всіх можливих елементарних подій ω називають простором елементарних подій, який позначають Ω. Наприклад, при підкиданні грального кубика простір елементарних подій утворюють події ωі = {випаде і очок}, і = 1, 2, 3, 4, 5, 6. Елементарні події, при появі яких відбувається певна подія, називають сприятливими для цієї події. Наприклад, при підкиданні грального кубика для події А={випаде парне число очок} сприятливими є елементарні події ω1, ω3, ω5. Кожну подію можна розглядати як деяку підмножину простору елементарних подій у даному випробуванні. Зокрема, подія А = Ω є достовірною, а подія В = ∅ — неможливою. Наприклад: Монету підкидають двічі. Для даного випробування описати простір елементарних подій. Розв'язання. При двократному підкиданні монети можливі чотири елементарних наслідки: (А, А); (А, Р); (Р, А); (Р, Р), де А — випадання аверса (зображення «герба»), Р — випадання реверса (зображення «номіналу»). Очевидно, вони утворюють повну групу подій, тому Ω = {(А, А); (А, Р);(Р, А); (Р, Р)} є простір елементарних подій даного випробування. Операції над подіями Сумою двох випадкових подій А і В називають таку подію, яка полягає в появі хоча б однієї з подій А або В, і позначають А + В (або А È В). Сумою п випадкових подій А1,А2,...,Аn називають таку подію, яка полягає в появі принаймні однієї з цих подій (позначається Добутком двох випадкових подій А і В називають таку подію, яка полягає в сумісній появі обох подій А і В, і позначають А • В (або А Ç В). Добутком п випадкових подій А1,А2,...,Ап називають таку подію, яка полягає в сумісній появі всіх цих подій (позначається Різницею двох випадкових подій А і В називають таку подію, яка полягає в виконанні події А і не виконанні події В, позначається як А – В, або А \ В. Подію Поняття суми і добутку подій можуть бути узагальнені на випадки будь-якого числа подій. З визначення операцій додавання і множення слідують співвідношення: 1) A + А = A; A ‧ А = A ; 2) A + U = U; A ‧ U = A; 3) A+ Æ = A ; A‧ Æ = Æ; 4) A + B = B + A ; A ‧ B = B ‧ A; 5) (A + B) + C = A + (B + C); (A ‧ B) ‧ C = A‧ (B ‧ C); 6) A ‧ (B + C) = A ‧ B + A ‧ C. Приклад 1. У ящику містяться кульки білого та чорного кольору. Навмання з нього виймають одну кульку. Подія А = {вийнято кульку білого кольору}, подія В = {вийнято кульку чорного кольору}. Сумісні чи несумісні ці події? Розв’язання. Ці події несумісні, тому що поява події А виключає виконання події В(кулька може бути або чорною або білою), також події А і В утворюють повну групу подій і є протилежні: Приклад 2. Підкидають два гральних кубики. Нехай події Аі = {випаде і очок на першому кубику}, і = 1, 2, 3,4, 5, 6, Bj = {випаде і очокна другому кубику}, і = 1, 2, 3,4, 5, 6. Виразити через Аі, і Bj такі події: а) сума очок на двох кубиках дорівнює п'яти; б) випаде в сумі хоча б десять очок; в) випаде в сумі не більше трьох очок. Розв'язання. а) Нехай С1= {сума очок на двох кубиках дорівнює п’яти}. Ця подія можлива тільки тоді, коли на першому кубику випаде і очок, а та другому j очок так, щоб і + j = 5, тобто і =1, j =4, або і = 2, j = 3, або і = 3, j = 2, або і = 4, j = 1. Отже, С1= А1• В4 + А2 • В3 + А3 • В2 + А4 • В1. б) Позначимо С2 = {випаде в сумі хоча б десять очок}. Подія С2 відбудеться тоді, коли на двох кубиках у сумі випаде або 10, або 11, або 12 очок, тобто і =4, j =6 або і =5, j =5 або і =6, j = 4 або і =6, j =5 або і =5, j =6 або і =6, j =6. Отже С2= А4• В6 + А5 • В5 + А6 • В4 + А6 • В5. + А6 • В6. + А5 • В6. в) Нехай Сз={випаде в сумі не більше трьох очок}. Оскільки найменша кількість очок, яка може випасти на кожному кубику, дорівнює одиниці, то подія Сз можлива лише тоді, коли сума очок на двох кубиках дорівнюватиме двом або трьом. Тому Сз = А1 • В1 + А2 • В1 + А1 • В2.. Приклад 3. Два стрільці роблять постріл у мішень по одному разу. Позначимо події А = {у мішень влучив перший стрілець}, В = {у мішеньвлучив другий стрілець}. Виразити через А і В такі події: С = {два влучення в мішень} D = {жодного влучення в мішень} Е = {хоча б одне влучення в мішень} F = {лише одне влучення в мішень}. Розв'язання. Простір елементарних подій складається з чотирьох подій А • В, Подія С відбудеться тоді, коли обидва стрільці влучать с мішень. Тому вона є добутком двох подій А і В. Отже С = А • В Подія D полягає в тому, що в мішень не влучить жодний стрілець, тобто не влучить ані перший ( Подія Е відбудеться тоді, коли влучить хоча б один стрілець. Це може бути толі, коли обидва стрільці влучать с мішень, або влучить перший, але не влучить другий, або не влучить перший, але влучить другий. Тоді лець. Це може бути тоді, коли або обидва стрільці влучать у мішень, або перший влучить, другий не влучить, або перший не влучить, а другий влучить. Тому Е = АВ + Подія F полягає в тому, що перший стрілець влучить в мішень, а другий не влучить, або другий влучить, а перший не влучить. Тому F = Приклади оформлення задач до розділу Задача 1.Два стрільці роблять по одному пострілу в мішень. Сумісні чи несумісні події А і В, якщо А = { перший стрілець влучив у мішень}, В = { другий стрілець влучив у мішень}. Відповідь.Сумісні. Задача 2.Перевірити, чи утворюють повну групу такі події: а) А = {випаде не менше трьох очок } В = {випаде більше трьох очок} у випробовуванні – підкиданні грального кубика б) А ={ один промах} В = { одне влучення} С = { два влучення} у випробовуванні, яке полягає в тому, що два стрільця роблять одному пострілу в мішень; в) А ={ випадання двох аверсів} В ={випадання хоча б одного реверсу} у випробовуванні – підкиданні двох монет. Відповідь.У всіх випадках події не утворюють повної групи подій і не є протилежними. Задача 3.Описати простір елементарних подій для випробування, яке полягає в підкиданні грального кубика. Відповідь. Ω = {ω1; ω2; ω3 ; ω4; ω5; ω6 }, де ωі ={випаде і очок}. Задача 4.Підкидають двічі гральний кубик. Нехай Аі = {випаде і очок при першому підкиданні} Ві = {випаде і очок при другому підкиданні } Виразити через Аі і Ві такі події: А = {обидва рази випаде парна кількість очок}, В = {сума очок при двох підкиданнях дорівнює 6}, С = { сума очок при двох підкиданнях більше 8}, D = {обидва рази випаде однакова кількість очок}. Відповідь.А = В=А1В5+ А2В4+ А3В3+ А4В2+ А5В1; С= А3В6+ А4В5+ А4В6+ А5В4+ А5В5+ А5В6+ А6В3+ А6В4+ А6В5+ А6В6; D= А1В1+ А2В2+ А3В3+ А4В4+ А5В5+ А6В6; Задача 5.Студент на екзамені відповідає на білет, у якому три питання. Нехай Аі = {студент відповів на і-те питання}. Виразити через Аі такі події: А ={Студент відповів принаймні на два питання }, В ={Студент не відповів на жодне питання }, С ={студент відповів тільки на одне питання }. Відповідь.А = С= Задача 6.Підкидають три монети. Для даного випробування записати простір елементарних подій і розкласти на елементарні такі події: А = {на двох монетах випаде «аверс»}, В = {на жодній монеті не випаде «реверс»}, С = {хоча б на одній монеті випаде «реверс»}. Відповідь. Ω = {(А, А, А); (А, А, Р); (А, Р, А); (А, Р, Р); (Р, А, А); (Р, А, Р);(Р, Р, А); (Р, Р, Р)}, А = {(А, А, Р); (А, Р, А); (Р, А, А)}; В = {(А, А, А)}; С = {(А, А, Р); (А, Р, А); (А, Р, Р); (Р, А, А); (Р, А, Р); (Р, Р, А); (Р, Р, Р)}. Задача 7.Стрілець виконує чотири постріли в мішень. Нехай подія Аі = {влучення в мішень при і-му пострілі}. Виразити через Аі такі події: А = {три влучення }, В = {хоча б один промах }, С = {не більше одного влучення }, D = {хоча б одне влучення}. Відповідь.А = В = С = D = Задача 8.Підкидають чотири рази монету. Розкласти на елементарні такі події: А = { на двох монетах випаде «аверс»} В = {випаде не більше одного «реверса» } Відповідь.А = {(А, А, Р, Р); (А, Р, А, Р); (А, Р, Р, А); (Р, А, А, Р); (Р, А, Р, А); (Р, Р, А, А)}, В = {(А, А, А, А); (А, А, А, Р);(А, А, Р, А); (А, Р, А, А);(Р, А, А, А)}.
Для самостійної роботи: Варіант 1 1. Перевірити, чи утворюють повну групу такі події: А = {випаде більше трьох очок }, В = {випаде не більше трьох очок} у випробовуванні – підкиданні грального кубика 2. Випробовування – з короба з шаховими фігурами відбирають навмання 1 фігуру. Позначимо події: А= {фігура чорного кольору}, В = {взята фігура - слон}. Чи сумісні події А і В, чи протилежні, чи утворюють повну групу подій? Виразити через А і В такі події: С= {фігура чорного кольору, але не слон}, D={фігура - слон чорного кольору}, Е={фігура – не слон білого кольору}. 3. Стрілець виконує три постріли в мішень. Нехай подія Аі = {влучення в мішень при і-му пострілі}. Виразити через Аі такі події: А = {три влучення }, В = {хоча б один промах }, С = {не більше одного влучення }, D = {хоча б одне влучення}. 4. Привести приклад випробовування і кількох подій до нього. Прокоментувати події, що є сумою, добутком, різницею приведених подій.
Варіант 2 1. Перевірити, чи утворюють повну групу такі події: А = {карта бубнова}, В = {карта – не туз} у випробовуванні – вийняти карту з колоди в 36 карт. 2. Випробовування – кидають ігровий кубик. Позначимо події: А= {випадає парне число очок}, В = {випаде число очок більше 3}. Чи сумісні події А і В, чи протилежні, чи утворюють повну групу подій? Виразити через А і В такі події: С= {випаде 4 або 6 очок}, D={випаде 2, 4, або 6 очок}, Е={випаде 2 очок}. 3. Студент на екзамені відповідає на білет, у якому три питання. Нехай Аі = {студент відповів на і-те питання}. Виразити через Аі такі події: А ={Студент відповів на два питання }, В ={Студент не відповів на жодне питання }, С ={студент відповів на всі питання }. 4. Привести приклад випробовування і кількох подій до нього. Прокоментувати події, що є сумою, добутком, різницею приведених подій.
Варіант 3 1. У випробовуванні – підкиданні двох монет позначимо події А ={ випадання двох реверсів} В ={випадання хоча б одного аверсу}. Перевірити, чи утворюють повну групу такі події. 2. Випробовування – виймають навмання карту з колоди в 36 карт. Позначимо події: А= {випадає бубнова карта}, В = {випаде карта числова (6-10)}. Чи сумісні події А і В, чи протилежні, чи утворюють повну групу подій? Виразити через А і В такі події: С= {карта – бубнова лялечка (валет, дама, король, туз)}, D={числова карта але не бубнова}. 3. Підкидають три рази монету. Розкласти на елементарні такі події: А = { на трьох монетах випаде «аверс»}, В = {випаде не більше одного «аверсу»}. 4. Привести приклад випробовування і кількох подій до нього. Прокоментувати події, що є сумою, добутком, різницею приведених подій.
Варіант 4 1. У випробовуванні – вибір студента в групі позначимо події А ={студент навчається на 4 і 5} В ={студент має борги}. Перевірити, чи утворюють повну групу такі події. 2. Випробовування – вибір навмання деталі з партії, серед яких є браковані та стандартні, крім того деталь виготовляється трьома виробниками – X, Y, Z. Позначимо події: В = {деталь – бракована}, X, Y, Z={деталь виготовлена виробником відповідно X, Y, Z}. Чи сумісні події X, Y, Z і В, чи протилежні, чи утворюють повну групу подій? Виразити через X, Y, Z і В такі події: E= {вибрана деталь стандартна і виготовлена виробником X або Y}, F={ вибрана деталь бракована і виготовлена виробником Х}. 3. В кошику фрукти 4-х видів: груші, яблука, банани та лимони. Випробовування– вибір навмання 3-х фруктів. Позначимо події Гі, Бі, Яі, Лі – і – кількість взятих груш, бананів, яблук або лимонів відповідно. Позначити через Гі, Бі, Яі, Лі події А ={взяті різні фрукти}, В={взято хоч одне яблуко}. 4. Привести приклад випробовування і кількох подій до нього. Прокоментувати події, що є сумою, добутком, різницею приведених подій.
Варіант 5 1. У випробовуванні – вибір потрібного потяга позначимо події А ={прибуває вранці} В ={прибуває вночі}, С ={прибуває вдень}. Перевірити, чи утворюють повну групу такі події. 2. На полиці стоять підручники з математики, фізики та хімії. Випробовування – вибір 2-х підручників навмання. Позначимо події: Мі, Фі, Хі – і – кількість взятих підручників з математики, фізики чи хімії. .Виразити через Мі, Фі, Хі такі події: E= {вибрані підручники з різних дисциплін}, F={вибрані підручники з однакових дисциплін }, G={серед вибраних підручників є хоч один з хімії }. 3. В двох шухлядах білі та чорні кулі. З обох шухляд навмання вибирають по одній кулі. Позначимо події: В1 – з першої шухляди вийнята біла куля, В2 – з другої шухляди вийнята біла куля, 4. Привести приклад випробовування і кількох подій до нього. Прокоментувати події, що є сумою, добутком, різницею приведених подій.
Варіант 6 1. Два студенти в книжковому магазині шукають потрібну книгу. Позначимо події: А ={книгу знайшов перший студент} В ={книгу знайшов другий студент}. Перевірити, чи утворюють повну групу такі події. 2. На полиці стоять підручники з математики, фізики та хімії. Випробовування – вибір 2-х підручників навмання. Позначимо події: М, Ф, Х– вибраний підручник відповідно з математики, фізики чи хімії. .Виразити через М, Ф, Хтакі події: E= {вибрані підручники з різних дисциплін}, F={вибрані підручники з однакових дисциплін }, G={серед вибраних підручників є хоч один з хімії }. 3. Підкидають двічі гральний кубик. Нехай Аі = {випаде і очок при першому підкиданні} Ві = {випаде і очок при другому підкиданні } Виразити через Аі і Ві такі події: А = {обидва рази випаде не парна кількість очок}, В = {сума очок при двох підкиданнях дорівнює 10}, С = { сума очок при двох підкиданнях менше 4}, D = {обидва рази випаде однакова кількість очок}. 4. Привести приклад випробовування і кількох подій до нього. Прокоментувати події, що є сумою, добутком, різницею приведених подій. Критерії оцінювання: 1-4бали – конспект приведених прикладів; Кожен розв’язаний приклад – 2 бали. Максимальна кількість балів – 12.
Поиск по сайту: |
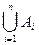 ).
). ).
).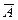 називають протилежною до події А в даному випробуванні, якщо вона відбувається, якщо не відбувається подія А, тобто
називають протилежною до події А в даному випробуванні, якщо вона відбувається, якщо не відбувається подія А, тобто 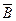 = А.
= А.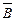 ). Тому D =.
). Тому D =. 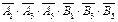 ;
; ; В=
; В=  ;
;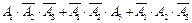 .
.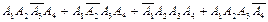 ;
; ;
;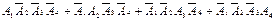 ;
; .
. – з першої шухляди вийнята не біла (чорна) куля,
– з першої шухляди вийнята не біла (чорна) куля, 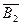 – з другої шухляди вийнята чорна куля. Скласти повну групу подій для визначеного випробовування, описуючи їх через елементарні події В1, В2.
– з другої шухляди вийнята чорна куля. Скласти повну групу подій для визначеного випробовування, описуючи їх через елементарні події В1, В2.