|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ВІДПОВІДІ ТАРЕЗУЛЬТАТИ ОБЧИСЛЕНЬ
Корисні рекомендації Для отримання найбільш точних та достовірних даних при обчисленні певних величин число десяткових знаків після коми не може бути меншим, ніж 4. Для Вашої зручності та для зручності викладача, який приймає цю роботу, в кінці цих методичних вказівок подана форма, яку потрібно заповнити та розмістити в кінці роботи (додаток А). Рекомендований вигляд титульної сторінки поданий у додатку Б. У додатку В поданий бланк завдання, котрий повинен бути заповнений та розміщений відразу після титульної сторінки. Організаційні вимоги Не виконувати якого-небудь із завдань не дозволяється! Увага! Розрахункова робота повинна бути здана до початку проведення другого модульного контролю! У випадку невчасної здачі розрахункової роботи бали за її виконання не виставляються. Увага! У випадку не написання, невчасної здачі роботи студент не допускається до складання іспиту! ЗАВДАННЯ 1 Відповідно до номера варіанта дати обґрунтовану (в тому числі графічну та за допомогою формул, якщо це можливо) відповідь на такі питання:
ЗАВДАННЯ 2
Дати правильну відповідь на такі питання, обґрунтовуючи цю відповідь:
1. Закон попиту передбачає, що: a) зростання доходів споживачів призведе до збільшення кількості придбаних благ; b) зростання ціни товару, зменшить обсяг запланованих закупівель; c) перевищення пропозиції над попитом знизить ціну; d) крива попиту має позитивний нахил. 2. Якщо ціна товару вища від ціни ринкової рівноваги, то виникає така ситуація: a) зростає безробіття; b) надлишок; c) дефіцит; d) зменшується попит і зростає пропозиція. 3. Який з перерахованих нижче факторів прямо не впливає на пропозицію; a) смаки й вподобання споживачів; b) ціни на ресурси; c) технологія виробництва; d) податки й дотації. 4. Якщо попит нееластичний, то: a) наслідком зростання ціни на 2% є зменшення величини попиту більш як на 2%; b) зростання ціни на 2% матиме наслідком зменшення величини попиту на 2%; c) зростання ціни на 2% матиме наслідком зменшення величини попиту менш як на 2%; d) наслідком зростання ціни на 2% є збільшення величини попиту менш як на 2%. 5. Всі комбінації ринкових кошиків, що пропонують однаковий рівень задоволення потреб споживача ілюструються за допомогою: a) кривої попиту; b) бюджетної лінії; c) кривої трансформації; d) кривої байдужості. 6. Максимальна кількість товару А, від якої треба відмовитись для споживання додаткової одиниці товару В називається: a) граничною нормою заміни; b) граничною нормою технічної заміни; c) граничною корисністю; d) граничною продуктивністю. 7. У міру збільшення споживання блага його гранична корисність, як правило: a) зменшується; b) збільшується; c) залишається незмінним; d) спочатку зростає, потім зменшується. 8. Всі комбінації праці та капіталу для виробництва одного й того самого обсягу продукції ілюструються за допомогою: a) кривої байдужості; b) ізокости; c) ізокванти; d) кривої попиту. 9. В короткостроковому періоді: a) рівень принаймні одного з ресурсів неможливо змінювати; b) не існує фіксованої кількості ресурсів; c) всі ресурси фіксовані; d) кількість праці неможливо змінювати. 10. Яке з наведених значень змін загальної корисності при збільшенні кількості спожитого товару ілюструє дію закону спадної граничної корисності: a) 200; 400; 700; 1000; b) 150; 350; 450; 600; c) 200; 250; 270; 280; d) 400; 500; 600; 700. 11. Для яких товарів перехресна еластичність дорівнює нулю: a) незалежних товарів; b) товарів-субститутів; c) товарів-комплементів; d) товарів Джіффена. 12. Якою є середня продуктивність праці при К = 4 для функції виробництва a) Q/L; b) 1; c) L/Q; d) 0,5Q/L. 13. Середня продуктивність змінного фактора виробництва – це: a) відношення сукупного продукту до кількості цього фактора, що зайнята у виробництві; b) загальний обсяг випуску продукції, який відповідає певній кількості змінного фактора за умови незмінності усіх інших факторів; c) збільшення сукупного продукту відносно до збільшення змінного фактора на одиницю; d) відношення граничного продукту до кількості змінного фактора, що зайнята у виробництві. 14. Досягнення максимального обсягу випуску при певній технології означає, що: a) гранична продуктивність дорівнює нулю, а середня продуктивність зменшується; b) середня і гранична продуктивності рівні; c) середня продуктивність досягла свого максимуму, а гранична дорівнює нулю; d) гранична продуктивність досягла свого максимуму при мінімальному значенні середньої продуктивності. 15. Негативна дія ефекту масштабу має місце, коли в результаті подвійного збільшення кількості залучених ресурсів: a) обсяг випуску продукції зростає більш як вдвічі; b) обсяг випуску продукції зростає вдвічі; c) обсяг випуску продукції зростає менш як вдвічі; d) обсяг випуску продукції не змінюється. 16. Всі можливі комбінації факторів виробництва при заданому обсязі витрат ілюструє: a) ізокоста; b) ізокванта; c) крива пропозиції; d) крива Енджела. 17. Середні змінні чи середні загальні витрати мінімальні, коли: a) граничні витрати від’ємні; b) вони дорівнюють граничним; c) граничні витрати досягають точки мінімуму; d) вони перетинаються із середніми постійними витратами. 18. Втрачений зиск від альтернативного використання ресурсів, що знаходяться у власності виробника – це: a) економічні витрати; b) явні витрати; c) альтернативна вартість ресурсів; d) загальні витрати. 19. У короткостроковому періоді конкурентна фірма, яка максимізує прибуток або мінімізує збитки, не буде продовжувати виробництво, якщо: a) ціна товару не покриває середніх загальних витрат; b) ціна товару менша мінімуму середніх змінних витрат; c) середні витрати вищі від ціни товару; d) ціна товару менша від граничних витрат. 20. Ринкове обмеження діяльності конкурентної фірми полягає в тому, що: a) фірма не має повної інформації про ринкову кон’юнктуру; b) відсутність можливості диференціювати продукцію; c) відсутність прибутку у довгостроковому періоді; d) відсутність можливості впливати на ціну. 21. У монополіста граничні витрати, як правило, менші від ціни продукції тому, що: a) ціна більша за граничний дохід; b) граничні витрати перевищують середні витрати; c) ціна менша за граничний дохід; d) граничні витрати менші від середніх витрат. 22. Якщо при певному обсязі виробництва граничні витрати фірми, яка працює в умовах монополістичної конкуренції, менші за її середні загальні витрати і дорівнюють граничному доходу, то це означає, що: a) фірма отримує прибутки; b) фірма досягла рівноважного обсягу виробництва; c) фірма зазнає збитків; d) правильної відповіді немає. 23. У моделі монополії вважається, що: a) вхід на ринок нових фірм не можливий; b) у покупців є альтернатива вибору іншого товару; c) виробляється стандартизована продукція; d) продавці і покупці сприймають ціни як задані. 24. В умовах рівноваги Курно: a) обсяг більший, ніж при змові, але менший ніж при досконалій конкуренції; ціна більша, ніж при досконалій конкуренції, але менша, ніж при змові; b) обсяг менший, ніж при змові, але більший ніж при досконалій конкуренції; ціна менша, ніж при досконалій конкуренції, але більша, ніж при змові; c) і ціна, і обсяг більші, ніж при змові; d) прибуток кожної фірми більший, ніж при змові. 25. Рівновага Курно – це: a) ситуація, коли встановлюється таке співвідношення обсягів виробництва кожної фірми, коли прибуток кожної з фірм максимальний, якщо інші фірми не змінюють обсягів виробництва; b) ситуація, коли встановлюється таке співвідношення обсягів виробництва кожної фірми, коли прибуток кожної з фірм максимальний, навіть якщо одна з фірм змінить обсяг виробництва; c) ситуація, коли встановлюється таке співвідношення обсягів виробництва кожної фірми, коли прибуток кожної з фірм більший, ніж прибуток, який могла б отримати кожна фірма, вступивши в змову; d) рівновага, яка досягається на ринку при змові. 26. Попит на ресурси залежить від: a) попиту на товар, що виготовлений за допомогою цих ресурсів; b) ціни ресурсів-замінників; c) продуктивності цих ресурсів; d) всі відповіді правильні. 27. Якщо в певному виробничому процесі капітал і праця виступають субститутами, то при зростанні ціни капіталу крива попиту на працю: a) зміщується праворуч; b) залишається без змін; c) зміщується ліворуч; d) стає вертикальною лінією. 28. Крива попиту на працю на конкурентному ринку збігається з: a) кривою граничних витрат на оплату праці; b) кривою граничного продукту праці; c) кривою граничного продукту праці у грошовому вираженні; d) кривою граничних витрат продукту, що виробляється. 1. Виробництво певного товару характеризується такими даними: a) більше праці і капіталу; b) менше праці і капіталу; c) більше праці, але менше капіталу; d) менше праці, але більше капіталу. 30. Яке з наведених тверджень, що стосується кривої граничних витрат у короткостроковому періоді, є неправильним: a) MC=AC, якщо АС набирають мінімального значення; b) якщо АС скорочуються, то МС менші за них; c) МС>АС у тому випадку, коли обсяг продукції більший за оптимальний; d) на розмір МС не впливають зміни цін на фактори виробництва. 31. Сума збитків фірми, яка закривається в короткостроковому періоді в умовах досконалої конкуренції: a) дорівнює змінним витратам; b) дорівнює нулю; c) дорівнює постійним витратам; d) не може бути визначена. 32. Бар’єром для вступу у галузь, де функціонує монополіст, можуть бути: a) патенти і ліцензії; b) більш низькі витрати крупного виробництва; c) законодавче оформлення виключних прав; d) все перелічене – правильне. 33. У стані довгострокової рівноваги фірма за умов монополістичної конкуренції: a) досягає виробничої ефективності; b) не досягає ні розподільної, ні виробничої ефективності; c) досягає розподільної ефективності; d) усі відповіді неправильні. 34. Якщо зростає частка затрат на ресурс у витратах фірми, то еластичність попиту на даний ресурс: a) збільшується; b) зменшується; c) не змінюється; d) можливий будь-який з варіантів. 35. Крива пропозиції прав на забруднення: a) має негативний нахил; b) абсолютно еластична; c) абсолютно нееластична; d) має позитивний нахил. ЗАВДАННЯ 3 За даними таблиці дати вичерпні відповіді на поставлені нижче питання:
N – номер варіанта. 1.Записати рівняння попиту і пропозиції та побудувати їхні криві. 2.Визначити точку ринкової рівноваги. 3.Встановити як зміниться ситуація на ринку, якщо ціна на товар буде: а) на 25+N грн вищою за рівноважну; і б) на 50– 0,01N² нижчою. Обрахувати. 4.Обчислити як зміняться рівноважні ціна і обсяг продукції, якщо: 1) попит зросте на 10% (для варіантів №1-17) чи попит зменшиться на 10% (для варіантів №18-35); 2) пропозиція зменшиться на 20% (для варіантів №1-17) чи пропозиція зросте на 20% (для варіантів №18-35). 5.Схематично проілюструвати як зміняться рівноважна ціна і рівноважний обсяг продукції, якщо:
a) знизяться доходи покупців; b) очікується зростання ціни товару; c) очікується зниження ціни товару; d) зросте число покупців товару; e) зменшиться число покупців товару; f) зростуть ціни на ресурси; g) знизяться ціни на ресурси; h) держава введе податок на продаж товару; i) держава надасть дотацію виробникам товару; j) на підприємствах галузі буде введена нова, більш прогресивна, технологія виробництва товару; k) фірми в галузі змушені перейти на стару технологію; l) підвищаться ціни на інші товари; m) знизяться ціни на інші товари; n) кількість продавців товару зросте; o) кількість продавців товару зменшиться; p) смаки споживачів змінились на користь товару; q) смаки споживачів стосовно товару погіршились; r) очікується зростання рівня доходів споживачів; s) очікується зниження рівня доходів споживачів. 6.Розрахувати коефіцієнти цінової еластичності попиту для всіх інтервалів цін і встановити відрізки еластичного та нееластичного попиту на кривій попиту. 7.Розрахувати дохід фірми за кожного рівня цін. 8.Встановити залежність динаміки доходу від еластичності попиту на основі побудови кривих доходу та попиту. 9.Визначити, при якій ціні дохід фірми міг би бути максимальним і визначити величину цього доходу. 10.Якщо фірма продає рівноважну кількість продукції за ціною ринкової рівноваги, то що вигідніше їй зробити для збільшення доходу – підвищувати чи знижувати ціну: а) на Z1 грн вищу за рівноважну; б) на Z2 грн нижчою за рівноважну. Примітка: інформацію про величини Z1 та Z2 викладач надає студенту тільки після виконання попередніх 9 пунктів і ніяким іншим чином.
Приклад розв’язування
Покажемо розв’язок цього завдання на прикладі варіанта № 36.
1.Записуємо рівняння попиту і пропозиції, пам’ятаючи, що їхні загальні рівняння мають такий вигляд: Для таблиці ΔР= –512,96. Отже,
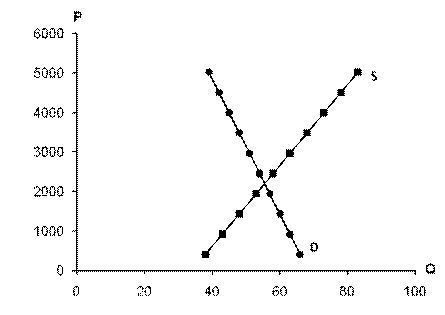
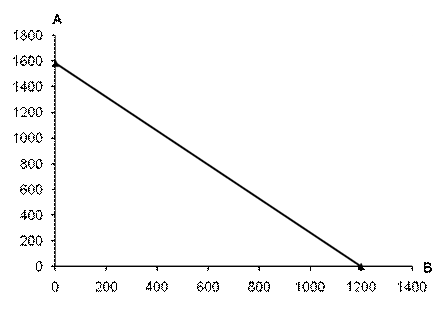
Будуємо криві попиту і пропозиції:
Рис. 3.1. Криві попиту і пропозиції
2.Визначаємо точку ринкової рівноваги. Як відомо в точці ринкової рівноваги QD = QS. Отже, прирівнюємо рівняння попиту і пропозиції:
3.Як зміниться ситуація на ринку, якщо ціна на товар буде: а) на 25 + N, тобто на 61 грн вищою за рівноважну. Р1 = 2201,76 + 61 = 2262,76 Обчислюємо:
QS > QD, отже на ринку утворився надлишок в розмірі: QS – QD = 0,95. б) на 50 – 0,01N², тобто на 37,04 грн нижчою за рівноважну. Р2 = 2201,76 – 37,04 = 2164,72 Обчислюємо:
QD > QS, отже на ринку утворився дефіцит в розмірі: QD – QS = 0,58. 4. а) якщо попит зменшиться на 10 %, то крива попиту переміститься вліво, а рівняння попиту набуде вигляду: Для визначення нового стану рівноваги потрібно нове рівняння попиту прирівняти до рівняння пропозиції. б) якщо пропозиція зросте на 20%, то крива пропозиції переміститься вправо, а рівняння пропозиції набуде вигляду: Для визначення нового стану рівноваги потрібно нове рівняння пропозиції прирівняти до рівняння попиту. 5.В даному завданні наведені конкретні зміни нецінових факторів попиту чи пропозиції, які треба проілюструвати на графіку, зазначаючи при цьому, як змінились ціна і кількість ринкової рівноваги, наприклад: “Зросли ціни на ресурси” – це неціновий фактор пропозиції, впливає на її зменшення.
Рис. 3.2. Зміна стану ринкової рівноваги в результаті зменшення пропозиції
Як видно з рис. 3.2. переміщення кривої пропозиції вліво призвело до зміни стану ринкової рівноваги, що супроводжується зростанням ціни рівноваги та зменшенням кількості рівноваги. 6.Розраховуємо коефіцієнти цінової еластичності попиту за формулою цінової еластичності попиту :
Як видно всі коефіцієнти еластичності
Рис. 3.3. Нееластичний попит 7.Розраховуємо дохід фірми за формулою:
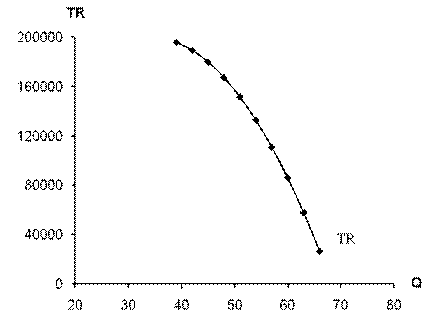
8.Будуємо криві доходу і попиту.
Рис. 3.4. Криві загального доходу і попиту Як видно з графіка зі зростанням обсягу продажу товару величина загального доходу зменшується. Пов’язано це з тим, що попит на продукцію фірми є нееластичним, тобто слабо реагує на зміну в ціні, і коли продавець зменшує ціну (зверху вниз по таблиці) на певний відсоток, то величина попиту хоча і реагує на це зростанням, однак на менший відсоток. В результаті такого зниження ціни продавець втрачає. При накладанні графіків видно, що вся крива попиту, на якій попит власне є нееластичним відповідає спадній криві доходу. 9.Знаючи, що найбільший дохід отримується, коли попит є одинично еластичним, тобто 10.Визначаємо, що вигідніше – підвищувати чи знижувати ціну фірмі. Це ми будемо визначати на підставі даних про зміну доходу. Насамперед визначимо який має дохід фірма при ціні ринкової рівноваги:
а) Отож, збільшуємо ціну на Z1 грн, а саме Обчислюємо QD:
Обчислюємо нове значення доходу:
Порівнюємо отримане значення доходу із початковим та робимо висновок про доцільність підняття ціни, обґрунтовуючи чому збільшення ціни призвело саме до такого результату. б) Зменшуємо ціну на Z2 грн, і тоді вона становитиме: Тоді Відповідно Також на основі порівняння початкового та отриманого значень доходів робимо висновок про доцільність зниження ціни та обґрунтовуємо свою думку. Робимо загальний висновок до пункту 10 про те, що потрібно робити фірмі із ціною для збільшення доходу. ЗАВДАННЯ 4
1.Певний споживач купує два товари А та В. Ціна товару А становить 2N грн., ціна товару В – 3N грн. На купівлю цих товарів він витрачає 100N²+100 грн. Функція загальної корисності споживача задана таким чином: На основі цих даних: Ø визначити, яку кількість товару А та товару В купить раціональний споживач; Ø яку величину задоволення отримає споживач; Ø записати рівняння бюджетної лінії та побудувати цю лінію; Ø показати на графіку стан рівноваги споживача. 2.Нехай ціна на товар А зростає на 10 грн. Визначити: Ø як зміниться структура оптимального споживчого кошика і величина задоволення споживача; Ø записати рівняння нової бюджетної лінії та побудувати її; Ø показати на графіку новий стан рівноваги споживача. 3.Визначити структуру оптимального споживчого кошика та величину витрат споживача, якщо споживач бажає отримувати той самий рівень задоволення, що він отримував до зростання ціни на товар А. На основі нових даних: Ø записати рівняння бюджетної лінії та побудувати її; Ø зобразити новий стан споживчої рівноваги. 4.В результаті проведених обрахунків у п. 1–3 встановити, коли діяли ефекти доходу та заміщення, і визначити їхні величини.
Приклад розв’язування
Покажемо розв’язок цього завдання на прикладі варіанта № 36.
1.Отже, споживач купує два товари А та В. Ціна товару А становить 72 грн., ціна товару В – 108 грн. На купівлю цих товарів він витрачає 129700 грн. Функція загальної корисності споживача задана таким чином: Для обчислення оптимального споживчого кошика, потрібно скористатись правилом максимізації корисності: Функції граничних корисностей кожного із товарів, MU, записують таким чином: Величина задоволення обчислюється з функції загальної корисності:
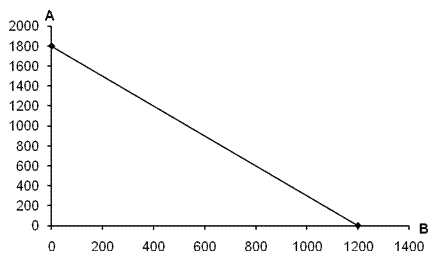
Рівняння бюджетної лінії має такий вигляд:
Нижче зображена ця бюджетна лінія.
Рис. 4.1. Бюджетна лінія
Виходячи із функції загальної корисності:
Рис. 4.2. Початковий стан рівноваги
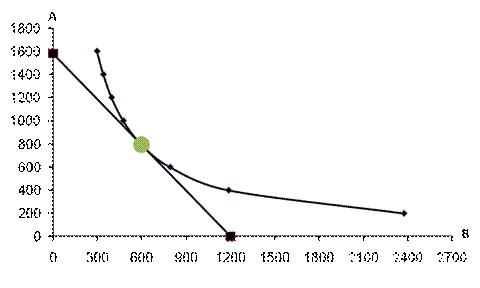
2.Нехай ціна на товар А зростає на 10 грн, тобто буде становити 82 грн. Зрозуміло, що зростання ціни на товар за незмінного рівня бюджету призведе до зміни до структури оптимального споживчого кошика. Для обчислення оптимального споживчого кошику за нової ціни треба здійснити всі аналогічні обчислення, що і в попередньому пункті. Отже, оптимальний кошик споживача складатиметься з 790,854 од. товару А, і 600,462 од. товару В, тобто зростання ціни товару А призвело до зниження споживання цього товару і до відповідної зміни структури споживчого кошика. Зрозуміло, що за меншої кількості товару А величина задоволення споживача зменшиться і буде становити: Нове рівняння бюджетної лінії матиме такий вигляд: Нижче зображена ця нова бюджетна лінія.
Рис. 4.3. Бюджетна лінія після зростання ціни товару А
За аналогією із попереднім пунктом будуємо модель рівноваги споживача після зростання ціни товару А.
Рис. 4.4. Новий стан рівноваги після зміни ціни товару А
3.Якщо споживач не бажає зменшувати величину свого задоволення, то абсолютно зрозуміло, що після зростання ціни товару А він повинен витрачати більше грошей. Для того, щоб визначити структуру оптимального споживчого кошика, треба записати систему з таких трьох рівнянь:
Розв’язками цієї системи є нова структура споживчого кошика: Аопт3=843,989; Вопт3=640,8, та величина витрат, потрібна для купівлі такої кількості товарів:
Рівняння цієї бюджетної лінії матиме такий вигляд: Нижче зображені нова бюджетна лінія та новий стан споживчої рівноваги.
Рис. 4.5. Бюджетна лінія після зростання ціни товару А і при більшому бюджеті споживача
Рис. 4.6. Новий стан рівноваги після зміни ціни товару А за незмінного рівня корисності 4.В результаті проведених обрахунків у п. 1–3 можна встановити, що діяли два ефекти: доходу і заміщення. Для обчислення кількісних величин цих ефектів треба пам’ятати, в чому їхня суть. Отже: ü ефект доходу показує, як впливає зміна ціни товару на реальний дохід споживача, і, отже, на кількість придбаного товару; при цьому номінальний дохід залишається незмінним, а кількість задоволення змінюється; ü ефект заміщення ілюструє вплив зміни ціни товару на його відносну ціну стосовно іншого товару, і відповідно на обсяг споживання; при цьому номінальний дохід змінюється, а рівень задоволення залишається незмінним. В початковій ситуації оптимальний кошик мав таку структуру: Аопт1=900,694; Вопт1=600,462. Згодом, після зростання ціни товару А, кількість обох товарів становила: Аопт2=790,854; Вопт2=600,462. Як видно, змінилась кількість товару А, тому в даному випадку спостерігається ефект доходу, який становитиме: 790,854–900,694=–199,84. Якщо ж споживач бажає отримувати початковий рівень задоволення, його кошик повинен виглядати таким чином: Аопт3=843,989; Вопт3=640,8. Порівняно з початковим кошиком змінились кількості обох товарів внаслідок зміни відносних цін, що свідчить про дію ефекту заміщення. Тому ефект заміщення, який спостерігається в даній ситуації, становитиме: для товару А: 843,989–900,694=–56,705 для товару В: 640,8–600,462=40,338.
ЗАВДАННЯ 5 Виробничий процес фірми характеризують такі дані: Ø β = 0,55 – N²/10000 (варіанти 1-14) або β = 0,7 – N²/10000 (варіанти 15-35); Ø α = 0,99 – β + N²/10000; Ø A = N +10. Використовуючи ці та інші дані виконати такі завдання: 1.На основі даних таблиці довести, що існує спадна віддача від праці, припускаючи, що приріст кількості праці становить початкове її значення. Проілюструвати спадну віддачу від праці на графіку.
2.На основі даних таблиці довести, що існує спадна віддача від капіталу, припускаючи, що приріст кількості капіталу становить початкове його значення. Проілюструвати спадну віддачу від капіталу на графіку.
3.На основі даних таблиці довести, що існує певний тип віддачі (залежно від того, якою є сума α + β стосовно 1).
4.Заповнити таблицю при умові, що кожне наступне значення L менше від попереднього на 10 (варіанти 1-5), на 8 (варіанти 6-14), на 6 (варіанти 15-35) та виконати такі завдання:
1)Записати рівняння виробничої функції та алгебраїчний вираз ізокванти. 2)Побудувати ізокванту, обчислити граничну норму технічної заміни для кожної точки ізокванти; 3)При цінах на ресурси: Примітка: значення Z3 можна отримати у викладача тільки після повного виконання завдань 3 та 4, а також завдання 5 включно із попереднім пунктом. 4)З’ясувати, чи є визначений в попередньому пункті рівень витрат найменшим, який потрібний для виробництва заданого обсягу при заданих комбінаціях праці і капіталу. Якщо так – побудувати відповідну модель виробництва певного обсягу продукції за найменших витрат. Якщо ні – визначити, якими повинні бути величини праці і капіталу, аби витрати були найменші, і відповідно побудувати модель виробництва за найменших витрат.
Приклад розв’язування
Покажемо розв’язок цього завдання на прикладі варіанта № 36.
Для нашого варіанту початкові дані мають вигляд: β = 0,5704; α = 0,5492; A = 46. 1.
Як видно, кількість праці зростає на однакову величину, а саме: ΔL=2,1026. В результаті збільшення кількості праці обсяг виробництва також зріс, проте темп приросту сповільнюється: ΔQ1=1745,767; ΔQ2=1371,015. За таких умов, коли збільшення кількості праці на певну фіксовану величину при незмінній кількості капіталу призводить до сповільнення зростання обсягу виробництва, існує спадна віддача від праці.
Рис. 5.1. Спадна віддача від праці 2.
Отже, з таблиці видно, що кількість капіталу зростає на однакову величину, а саме: ΔК=3,83. Кількість праці при цьому залишається незмінною. В результаті нарощування кількості капіталу обсяг виробництва зростає, однак темп приросту сповільнюється: ΔQ1=2501,679; ΔQ2=1970,857. За таких умов говорять про спадну віддачу від капіталу.
Рис. 5.2. Спадна віддача від капіталу 3.
В даному випадку α + β = 1,1196 > 1, отже, повинна існувати віддача від масштабів, що зростає. Це доводиться таким чином. Як видно з таблиці, кількість вхідних ресурсів: праці і капіталу, – зростає вдвічі. Обсяг виробництва, проте, зростає більше, як вдвічі, а саме: Q2/Q1=2,172867>2 Q3/Q2=2,172867>2 Отже, існує зростаюча віддача від масштабів. 4.
1) Щоб записати рівняння виробничої функції потрібно початкові дані підставити у виробничу функцію Кобба-Дугласа, зокрема: Для запису алгебраїчного виразу ізокванти, потрібно у виробничу функцію підставити значення Q з таблиці та виразити L через K чи навпаки. 2) Будуємо ізокванту:
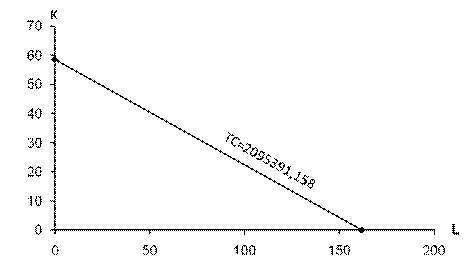
Рис. 5.3. Ізокванта Обчислюємо граничну норму технічної заміни для кожної точки ізокванти, використовуючи таку формулу: 3) При PL = 12960; PK = 35795,52 визначаємо витрати виробництва для кожної з комбінацій праці і капіталу. Витрати виробництва визначаються за такою формулою: Отже, TC1=2114344,03; TC2=2100122,254; TC3=2095391,158; TC4=2102430,766; TC5=2124311,596; TC6=2165268,688; TC7=2231309,704; TC8=2331247,584; TC9=2478548,378. Серед усіх визначених значень витрат мінімальним є значення TC3. Таке значення досягається при такій комбінації праці і капіталу: L=82; К=28,8491732. Рівняння ізокости матиме такий вигляд: Будуємо цю ізокосту:
Рис. 5.4. Ізокоста 4) Щоб з’ясувати, чи є обчислений в попередньому пункті рівень витрат найменшим, потрібно скористатись правилом найменших витрат:
Примітка. Зверніть увагу на важливість правильного обчислення показників у контексті необхідної мінімальної кількості десяткових знаків після коми. У випадку недотримання цієї поради у Ви можете отримати неправдиві результати та зробити неправдиві висновки. Тому, виходячи з рівності В результаті обчислень ми отримаємо такі оптимальні значення праці та капіталу: Lопт=82,3706; Копт=28,7144. Оптимальне, тобто міняльна значення витрат, становитиме:
Рівняння ізокости матиме такий вигляд: Будуємо модель виробництва за найменших витрат.
Рис. 5.5. Модель виробництва за найменших витрат ЗАВДАННЯ 6
Використовуючи дані, що характеризують діяльність фірми, яка працює в умовах недосконалої конкуренції в довгостроковому періоді: 1.Визначити при якому обсязі виробництва і ціні фірма матиме максимальний прибуток і визначити величину цього прибутку. 2.Побудувати криві середніх, граничних витрат, граничного і середнього доходів. 3.Побудувати модель максимізації прибутку за допомогою порівняння загального доходу і загальних витрат, а також за допомогою порівняння граничних витрат та граничного доходу. 4.Проаналізувати залежність між загальним і граничним доходами.
Початкові дані:
Приклад розв’язування
Покажемо розв’язок цього завдання на прикладі варіанта № 36.
Заповнюючи таблицю, треба пам’ятати, що на ринку недосконалої конкуренції ціна не є фіксованою величиною для окремої фірми, а певною мірою залежить від цієї фірми. Для того, щоб заповнити 4 колонку потрібно скористатись рівнянням попиту: Примітка: визначаючи величини MR та MC у таблиці, краще скористатись функціями MR та MC, а саме: MR=TR´ та MC=TC´. 1.Якщо дивитись на результати обчислень у таблиці, то максимальний прибуток в розмірі 860,4 досягається при ціні 288 грн. і обсязі виробництва 4 одиниці. Проте чи є цей прибуток найбільшим. Для цього треба скористатись правилом максимізації прибутку: 2.Будуємо криві середніх та граничних витрат, а також криві середнього і граничного доходів.
Рис. 6.1. Криві середніх і граничних витрат
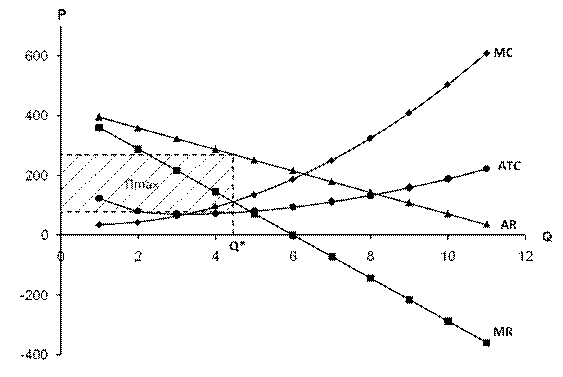
Рис. 6.2. Криві граничного і середнього доходів 3.Будуємо моделі максимізації прибутку.
Рис. 6.3. Максимізація прибутку фірмою, яка працює в умовах недосконалої конкуренції, за методом порівняння загальних витрат і загального доходу Як видно з графіка крива загального доходу до певного обсягу виробництва лежить над кривою загальних витрат, тобто дохід при цих обсягах виробництва повністю покриває загальні витрати, і фірма отримує прибутки. Максимальний прибуток досягається в точці, де відстань по вертикалі між кривими загального доходу і загальних витрат є найбільшою. Ця точка визначається в попередньому пункті. Зрештою найбільший прибуток можна дослідити і за кривою прибутку.
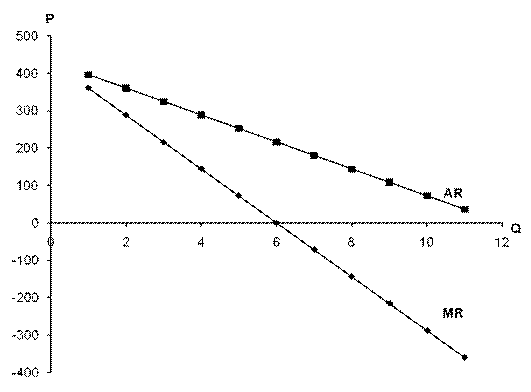
Рис. 6.4. Максимізація прибутку фірмою, яка працює в умовах недосконалої конкуренції, за методом порівняння граничних витрат і граничного доходу
Як видно з рис. 6.4. фірма максимізує прибуток при обсязі виробництва Q*, що визначається точкою перетину MR і MC; крива попиту (AR) лежить над кривою середніх загальних витрат, отже ціна є більшою від середніх витрат і фірма отримує прибуток. Прибуток показаний площею заштрихованого прямокутника і обчислюється таким чином: 4.Для пояснення залежності між загальним і граничним доходом побудуємо їхні криві.
Рис. 6.5. Залежність між загальним і граничним доходами Дивлячись на графік, ми бачимо, що коли граничний дохід є додатнім, загальний при цьому зростає, і коли граничний дохід стає від’ємним, загальний дохід реагує на це зменшенням. При нульовому значення граничного доходу загальний дохід досягає свого максимуму. ЗАВДАННЯ 7 В таблиц
Поиск по сайту: |
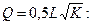
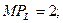

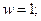
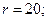
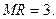 Щоб отримати максимальний прибуток фірма повинна використовувати:
Щоб отримати максимальний прибуток фірма повинна використовувати: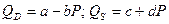 .
.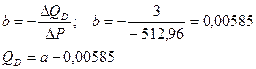 Визначаємо вільний член “а”, підставляючи у рівняння будь-яку комбінацію QD i P з таблиці:
Визначаємо вільний член “а”, підставляючи у рівняння будь-яку комбінацію QD i P з таблиці:
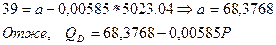
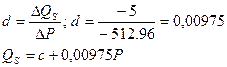 Визначаємо вільний член “с”, підставляючи у рівняння будь-яку комбінацію QS i P з таблиці:
Визначаємо вільний член “с”, підставляючи у рівняння будь-яку комбінацію QS i P з таблиці:

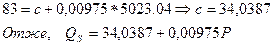



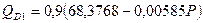 .
.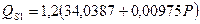 .
.
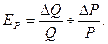
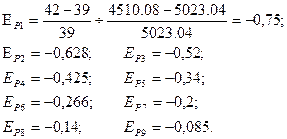
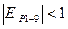 . Це означає, що попит є нееластичним впродовж усієї кривої попиту, тобто на усіх відрізках, що задані за умовою. Нееластичний попит зображено на рис. 3.3.
. Це означає, що попит є нееластичним впродовж усієї кривої попиту, тобто на усіх відрізках, що задані за умовою. Нееластичний попит зображено на рис. 3.3.
 .
.
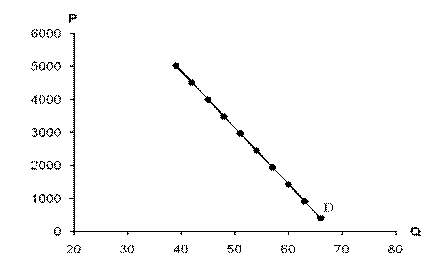
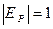 , враховуючи формулу еластичності:
, враховуючи формулу еластичності: 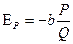 , – а також беручи до уваги рівняння попиту обчислюємо ціну, при якій дохід максимальний, а згодом і сам дохід.
, – а також беручи до уваги рівняння попиту обчислюємо ціну, при якій дохід максимальний, а згодом і сам дохід.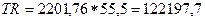 – це дохід, з яким будуть порівнюватись всі наступні зміни.
– це дохід, з яким будуть порівнюватись всі наступні зміни. .
.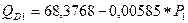 .
. .
.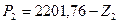 .
. .
. .
.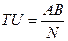 .
.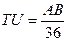 .
.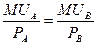 .
. . Використовуючи також бюджетне обмеження:
. Використовуючи також бюджетне обмеження: 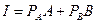 , – потрібно записати систему цих двох рівнянь і обчислити оптимальні значення товарів. В нашому випадку: Аопт1=900,694; Вопт1=600,462.
, – потрібно записати систему цих двох рівнянь і обчислити оптимальні значення товарів. В нашому випадку: Аопт1=900,694; Вопт1=600,462.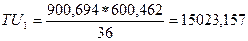
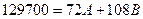 .
.

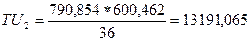 .
.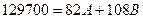 .
.
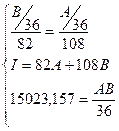
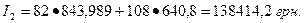
 .
.

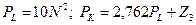 , – визначити витрати виробництва для кожної величини праці і капіталу. Встановити серед усіх визначених значень витрат мінімальне та вказати комбінацію праці і капіталу, при якій досягається такий рівень витрат. Для визначеного рівня витрат записати рівняння ізокости та зобразити її графічно.
, – визначити витрати виробництва для кожної величини праці і капіталу. Встановити серед усіх визначених значень витрат мінімальне та вказати комбінацію праці і капіталу, при якій досягається такий рівень витрат. Для визначеного рівня витрат записати рівняння ізокости та зобразити її графічно.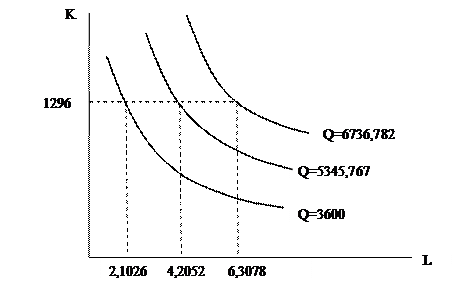
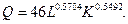

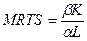 .
.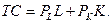
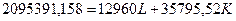 .
.
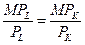 . Для спрощення дане правило записують в такому форматі:
. Для спрощення дане правило записують в такому форматі: 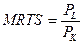 . Отже, в нашому випадку виявлено, що для виробництва заданого обсягу продукції при виявленій комбінації праці і капіталу: L=82; К=28,8491732, – дана рівність не досягається, тобто:
. Отже, в нашому випадку виявлено, що для виробництва заданого обсягу продукції при виявленій комбінації праці і капіталу: L=82; К=28,8491732, – дана рівність не досягається, тобто: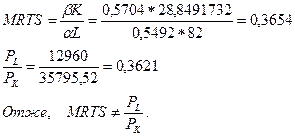
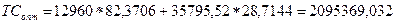 .
.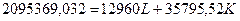 .
.
 ;
;  ;
; 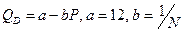 .
.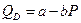 .
.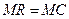 . Як видно при даному обсязі виробництва MR = 180, а MC = 77,4. Зрозуміло, що ці величини не рівні. Тому потрібно проводити обчислення далі для обчислення оптимального значення ціни та обсягу виробництва, при яких прибуток буде максимальним. Для цього знову ж таки користуємось рівністю
. Як видно при даному обсязі виробництва MR = 180, а MC = 77,4. Зрозуміло, що ці величини не рівні. Тому потрібно проводити обчислення далі для обчислення оптимального значення ціни та обсягу виробництва, при яких прибуток буде максимальним. Для цього знову ж таки користуємось рівністю 

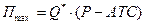 .
.