 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Моменти інерції за повороту осей. Головні осі та головні моменти інерції
ТЕМА 4 (лекції 8,9) ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ
Статичні моменти та моменти інерції плоских фігур
:
де Осьові моменти інерції:
Подібно, як і у випадку статичних моментів, вирази (4.3) можна записати і в іншому вигляді:
де
Відцентровим моментом інерції
Відношення осьових моментів інерції до величин, що виражають найбільшу відстань граничної точки перерізу до відповідної осі називаються осьовими моментами опору плоскої фігури:
Тут Полярним моментом опоруплоскої фігури називається величина
де
Моменти інерції та моменти опору деяких простих фігур Прямокутник, квадрат.Знайдемо момент інерції прямокутника з основною
Рис. 4.2
Для визначення величини
і, очевидно,
Так само отримаємо
Моменти опору будуть, відповідно:
Для квадрата із стороною
Круг. Кругове кільце. Розглянемо круг діаметром
Полярний момент інерції круга
Для визначення осьових моментів круга скористаємось рівнозначністю осей
Для визначення моментів опору круга скористаємось формулою
Тоді
Рис. 4.3 Для визначення полярного моменту інерції кругового кільця (рис. 4.3) із зовнішнім діаметром
Формули для осьових моментів інерції кільця наступні:
Відповідні формули для моментів опору кільця знайдемо на основі формул (4.13) – (4.15):
Визначення статичних моментів та осьових моментів інерції складних перерізів, що складаються із простих (коло, прямокутник, трикутник) вимагає більш складніших розрахунків та використання формул паралельного переносу та повороту осей координат фігури. Геометричні характеристики типових перерізів зведені в табл. 4.1.
Таблиця 4.1 – значення геометричних характеристик деяких типових перерізів
4.3. Моменти інерції за паралельного переносу Розглянемо плоску фігуру з площею
  
a) б) Рис. 4.4
Враховуючи, що перший інтеграл рівності (4.16) дорівнює моменту інерції
Так само можна показати, що
Аналізуючи виведені формули, можна прийти до висновку, що момент інерції плоскої фігури відносно довільної осі завжди буде більшим від момента інерції відносно центральної осі, що паралельна першій.
Моменти інерції за повороту осей. Головні осі та головні моменти інерції Візьмемо довільну плоску фігуру, моменти інерції якої відносно осей координат
Необхідно знайти величини
де Тоді основний момент
Після відповідних перетворень:
Аналогічно, для інших моментів інерції будемо мати:
Із формул (4.21), (4.22) неважко зауважити, що сума Аналіз формули (4.23) показує, що зміна відцентрового моменту Такі осі координат називаються головними осями інерції. А якщо початок координат співпадає з центром ваги фігури, то такі осі будуть називатися головними центральними осями. Шляхом диференціювання за змінною
Аналізуючи попередній абзац, можна зробити висновок, що головними, являються ті осі, для яких осьові моменти інерціїприймають найбільшічи найменші значення. Формули для знаходження головних моментів інерції будуть наступними:
Виключивши з цих формул величини
Тут величиною Запитання для самоконтролю 1. Які Ви знаєте геометричні характеристики плоских перерізів? 2. Що таке статичний момент плоскої фігури? 3. Яка розмірність осьових моментів інерції? 4. Дайте визначення осьового моменту опору плоскої фігури. 5. Дайте визначення полярного моменту інерції. 6. Які значення може приймати відцентровий момент інерції плоскої фігури? 7. Що таке полярний момент опору плоскої фігури? 8. Запишіть моменти інерції та опору прямокутника. 9. Запишіть полярний момент інерції та полярний момент опору круга. 10. Як знаходиться полярний момент інерції кільця 11. Визначення осьових моментів інерції за паралельного переносу осей. 12. Що є інваріантом в залежностях між осьовими моментами інерції? 13. Які осі координат називаються головними центральними осями? 14. Які осьові моменти інерції називаються головними?
Поиск по сайту: |
 ,
,  . (4.1)
. (4.1) ,
, 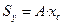 , (4.2)
, (4.2) ,
,  – координати центра ваги фігури.
– координати центра ваги фігури. ,
,  . (4.3)
. (4.3) ,
, 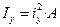 , (4.4)
, (4.4) ,
,  – середні значення ординат до відповідних осей, які ще називають радіусами інерції перерізу.
– середні значення ординат до відповідних осей, які ще називають радіусами інерції перерізу. . (4.5)
. (4.5)
 . (4.6)
. (4.6) . (4.7)
. (4.7) ,
, 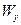 – відповідно моменти опору фігури відносно осей
– відповідно моменти опору фігури відносно осей  і
і  ;
; 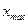 ,
,  – відстань від осей до найвіддаленіших точок фігури.
– відстань від осей до найвіддаленіших точок фігури.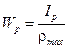 , (4.8)
, (4.8) – відстань від початку координат до найвіддаленішої точки фігури.
– відстань від початку координат до найвіддаленішої точки фігури. і висотою
і висотою  відносно осей
відносно осей 
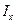 скористаємося формулами (4.3). Двома нескінченно близькими одна до одної прямими виріжемо елементарну смужку з основою
скористаємося формулами (4.3). Двома нескінченно близькими одна до одної прямими виріжемо елементарну смужку з основою  , що знаходиться на відстані
, що знаходиться на відстані  від осі
від осі 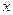 . Її площа
. Її площа  рівна
рівна
 . (4.9)
. (4.9) . (4.10)
. (4.10)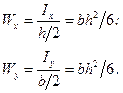 (4.11)
(4.11) отримаємо:
отримаємо: (4.12)
(4.12) (рис. 4.2, б). Двома концентричними колами з радіусами
(рис. 4.2, б). Двома концентричними колами з радіусами  і
і  , виріжемо елементарну площинку з площею
, виріжемо елементарну площинку з площею .
. . (4.13)
. (4.13)
 .
. .
.
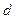 використаємо формулу (4.13) з інтегруванням у межах від
використаємо формулу (4.13) з інтегруванням у межах від  до
до  , тобто
, тобто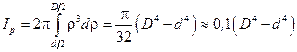 . (4.14)
. (4.14)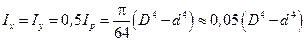 . (4.15)
. (4.15) ,
, 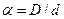 ;
; .
.

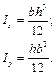
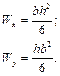





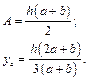

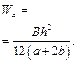
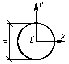


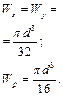







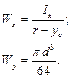


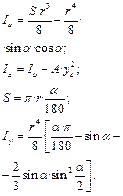







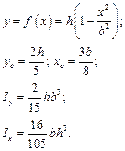
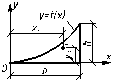
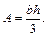
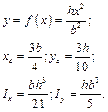
 , віднесену до довільної прямокутної системи координат
, віднесену до довільної прямокутної системи координат  (рис. 4.3). Нехай точка
(рис. 4.3). Нехай точка  є центром ваги цього перерізу, а осі
є центром ваги цього перерізу, а осі  і
і  . Тоді, за означенням (4.3), момент інерції
. Тоді, за означенням (4.3), момент інерції  відносно осі
відносно осі 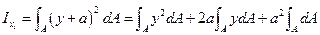 . (4.16)
. (4.16) . (4.17)
. (4.17) , (4.18)
, (4.18) .
. відомі і записуються у вигляді:
відомі і записуються у вигляді: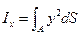 ,
,  ,
,  . (4.19)
. (4.19) ,
,  відносно повернутих осей
відносно повернутих осей  ,
, 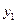 (рис. 4.3, б). Після повороту осей нові координати елементів площі
(рис. 4.3, б). Після повороту осей нові координати елементів площі  ,
,  , (4.20)
, (4.20) – кут повороту.
– кут повороту.
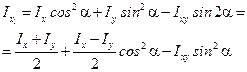 (4.21)
(4.21)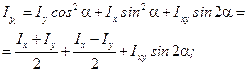 (4.22)
(4.22)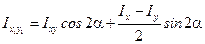 . (4.23)
. (4.23) є величиною сталою і дорівнює полярному моменту інерції фігури відносно початку координат.
є величиною сталою і дорівнює полярному моменту інерції фігури відносно початку координат. до
до 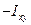 . Тобто, при певному повороті координатних осей
. Тобто, при певному повороті координатних осей 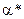 відцентровий момент інерції
відцентровий момент інерції  перетворюється на кут в нуль.
перетворюється на кут в нуль.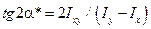 . (4.24)
. (4.24)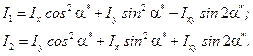 . (4.25)
. (4.25) та
та  , після низки перетворень, отримаємо значення максимального і мінімального моментів інерції:
, після низки перетворень, отримаємо значення максимального і мінімального моментів інерції: . (4.26)
. (4.26)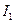 позначається більший з двох головних моментів інерції, а величиною
позначається більший з двох головних моментів інерції, а величиною  – менший. Ураховуючи, що сума осьових моментів інерції відносно двох взаємно перпендикулярних осей перерізу є величиною сталою, можна дійти висновку, що в цьому випадку момент інерції
– менший. Ураховуючи, що сума осьових моментів інерції відносно двох взаємно перпендикулярних осей перерізу є величиною сталою, можна дійти висновку, що в цьому випадку момент інерції