 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вектори, лінійні операції над векторами
ЛЕКЦІЯ 6. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ ПЛАН 1. Системи координат 2. Вектори, лінійні операції над векторами 3. Скалярний, векторний, мішаний добуток векторів Системи координат Три взаємно перпендикулярні осі Ох, Оу, Оz, які мають спільний початок точку О і однакову масштабну одиницю, утворюють прямокутну декартову систему координат у просторі. Якщо таких осей дві: Ох і Оу, то маємо систему координат на площині.
Рис. 2.
Осі Ох, Оу, Оz називаються відповідно осями абсцис, ординат і аплікат, точка О — початок системи координат. Нехай М — довільна точка в просторі або на площині. Декартовими координатами x, y, z точки М називатимемо відповідно довжини ОА, ОВ, ОС напрямлених відрізків Таким чином, кожній точці простору відповідає впорядкована трійка чисел (x, y, z), а на площині — впорядкована пара чисел (x, y), тобто встановлюється відповідність між геометричним образом — точкою і впорядкованою множиною чисел. Ця відповідність дає можливість використовувати рівняння для відображення геометричних образів, таких як лінія, площина тощо, та застосовувати алгебраїчні методи для розв’язування геометричних задач. Полярна система координат складається з деякої точки площини О, яка називається полюсом, променя ОА, що виходить з цієї точки і називається полярною віссю. Крім того, задається одиниця масштабу для вимірювання довжин відрізків.
Рис. 4 Полярними координатами точки М називаються числа r — відстань від полюса О до точки М і j — кут, на який треба повернути полярну вісь ОА до її збігу з ОМ, проти годинникової стрілки. Полярний радіус Зв’язок між полярними і декартовими координатами точки (рис. 4) встановлюють формули:
Приклад. Знайти полярні координати точки М (2, 2). З формули (2.1) маємо Розглянемо такі перетворення систем координат: 1) паралельний зсув осей, коли змінюється положення початку системи координат, а напрям осей залишається таким самим; 2) поворот осей, коли обидві осі повертаються на деякий кут відносно початку системи координат.
1. Нехай точка М у старій системі координат Оху має координати (х, у), а в новій системі координат
де (х0, у0) — декартові координати початку нової системи координат (точка О´) у старій системі координат. Розв’язуючи рівняння (1.2) відносно 2. Повернемо тепер стару систему координат Оху відносно точки О на кут a і дістанемо нову систему Ох¢y¢ (рис. 6). Розглянемо також дві полярні системи координат з полюсом у точці О і полярними осями Ох і Ох¢. Тоді згідно з рис. 6 маємо
Крім того, g = a + b, підставляючи це значення gу формули, остаточно будемо мати:
Розв’язуючи рівності (1.3) відносно
Здобуті формули відбивають зв’язок між старими (x, y) і новими Вектори, лінійні операції над векторами Означення. Вектором називається напрямлений відрізок. Позначати вектори будемо Вектор, в якого початок і кінець збігаються, називається нульовим вектором. Вектор вважається заданим, коли відома його довжина Два вектори Вектори 1) колінеарні; 2) однаково напрямлені; 3) їхні довжини рівні. З останнього випливає, що при паралельному перенесенні вектора дістаємо новий вектор, що дорівнює попередньому, тому вектори в аналітичній геометрії називають вільними. Нехай у просторі задано деяку вісь l і вектор
Означення. Проекцією вектора Позначається проекція вектора прl де Якщо розглянути прямокутну декартову систему координат і точки початку А (х1, у1, z1) і кінця В (х2, у2, z2) вектора Ох: ах = х2 – х1, Оу: ау = у2 – у1, Оz: аz = z2 – z1. Довжина вектора подається формулою:
Якщо позначити a, b, g — кути між вектором
У подальшому називатимемо їх напрямними косинусами вектора cos2a + cos2b + cos2g = 1. Дії з векторами виконуються за правилами: 1. Додавання:
2. Множення вектора на число a Î R:
Для лінійних операцій з векторами виконуються властивості: 1. 2. 3. 4. 5. Теорема. Проекція суми двох векторів на вісь дорівнює сумі їхніх проекцій на цю вісь:
Теорема. При множенні вектора на число його проекція на цю вісь також множиться на це число:
Нехай вектори
3. Скалярний, векторний, мішаний добуток векторів Означення. Скалярним добутком двох ненульових векторів Отже:
де j — кут між векторами. Використовуючи формулу проекції вектора, можна також записати:
Властивості скалярного добутку: 1. 2. 3. 4. 5. Нехай вектори
Отже, З рівності (1.7) випливає, що: 1. Необхідною і достатньою умовою перпендикулярності векторів 2. Кут між двома векторами
Означення. Векторним добутком вектора 1) довжина вектора 2) вектор
3) вектор Модуль векторного добутку двох неколінеарних векторів дорівнює площі паралелограма, побудованого на векторах як на сторонах. Властивості векторного добутку: 1. 2. 3. 4. Знайдемо векторні добутки одиничних векторів
Знайдемо координати вектора
або
Означення. Мішаним добутком векторів Розглянемо геометричний зміст мішаного добутку. Для цього побудуємо на векторах Знайдемо об’єм паралелепіпеда, побудованого на векторах
З останнього випливає, що модуль мішаного добутку чисельно дорівнює об’єму паралелепіпеда, побудованого на векторах
Враховуючи формули (1.7) і (1.8) знаходження скалярного і векторного добутків, маємо:
або
Властивості мішаного добутку: 1. 2.
Поиск по сайту: |
 Рис. 1
Рис. 1


 Рис. 3
Рис. 3

 може змінюватись у межах
може змінюватись у межах 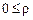 < ∞, полярний кут, як правило, змінюється в межах
< ∞, полярний кут, як правило, змінюється в межах  <
<  .
. (1.1)
(1.1) , tgj = 1. Згідно з останньою рівністю
, tgj = 1. Згідно з останньою рівністю  , або
, або  , але у = 2 > 0 і х = 2 > 0, маємо
, але у = 2 > 0 і х = 2 > 0, маємо 
 Рис. 5
Рис. 5
 Рис. 6
Рис. 6 —
—  . Знайдемо зв’язок між ними. З рис. 2.5 бачимо, що
. Знайдемо зв’язок між ними. З рис. 2.5 бачимо, що , (1.2)
, (1.2) і
і  , маємо
, маємо  .
. .
. (1.3)
(1.3)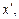
 дістаємо:
дістаємо: = х cosa + y sina,
= х cosa + y sina,  = – х sina + y cosa.
= – х sina + y cosa. координатами точки.
координатами точки. . Якщо, скажімо, точка А — початок вектора, а точка В — його кінець, то маємо
. Якщо, скажімо, точка А — початок вектора, а точка В — його кінець, то маємо  .
. ,
,  і напрям щодо деякої осі.
і напрям щодо деякої осі. і
і  називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих. і
і  .
. Рис. 7
Рис. 7
 на вісь l називається довжина
на вісь l називається довжина 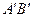 напрямленого відрізка
напрямленого відрізка  на осі l. Слід зазначити, що
на осі l. Слід зазначити, що  , якщо напрям
, якщо напрям  збігається з напрямом l і
збігається з напрямом l і  , якщо напрям
, якщо напрям  ,
, — кут між вектором і віссю.
— кут між вектором і віссю. (1.4)
(1.4)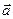 і відповідними осями системи координат, то їх косинуси можна знайти за формулами:
і відповідними осями системи координат, то їх косинуси можна знайти за формулами: . (1.5)
. (1.5) = (ах + bх, ау + bу, аz + bz).
= (ах + bх, ау + bу, аz + bz). .
. .
. .
. .
. .
. .
.

 такі, що за напрямом збігаються відповідно з осями Ох, Оу, Оz і
такі, що за напрямом збігаються відповідно з осями Ох, Оу, Оz і  . Такі вектори надалі називатимемо одиничними векторами осей системи координат. Тоді
. Такі вектори надалі називатимемо одиничними векторами осей системи координат. Тоді (1.6)
(1.6) і
і  називається число (скаляр), яке дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
називається число (скаляр), яке дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.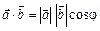 ,
, .
. .
. .
.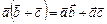 .
. .
. якщо
якщо  і навпаки,
і навпаки,  .
. маємо:
маємо: (1.7)
(1.7)
 є ах bх + ау bу + аz bz = 0.
є ах bх + ау bу + аz bz = 0. .
. , якщо:
, якщо: , де j — кут між двома векторами;
, де j — кут між двома векторами; перпендикулярний до кожного з векторів
перпендикулярний до кожного з векторів 
 Рис. 8
Рис. 8
 , якщо
, якщо  і
і  — колінеарні вектори.
— колінеарні вектори. .
.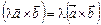 .
. .
. . З колінеарності векторів випливає:
. З колінеарності векторів випливає:  . З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
. З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
 , якщо
, якщо  ,
, 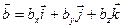 .
.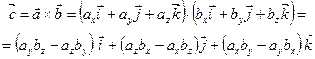 (1.8)
(1.8) .
. Рис. 9
Рис. 9
 називається число, яке дорівнює скалярному добутку вектора
називається число, яке дорівнює скалярному добутку вектора  і
і  , тобто
, тобто 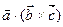 .
. , вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
, вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
 . Висота дорівнює
. Висота дорівнює  . Отже, остаточно маємо:
. Отже, остаточно маємо: . (1.9)
. (1.9) .
. .
.
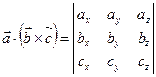 .
. .
. .
.