 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Власні числа і власні вектори матриці
ЛЕКЦІЯ 5. N-ВИМІРНИЙ ВЕКТОРНИЙ ПРОСТІР ПЛАН 1. Основні поняття 2. Зв’язок між базисами 3. Лінійні перетворення 4. Власні числа і власні вектори матриці Основні поняття Означення 1. Сукупність упорядкованих систем з n дійсних чисел, для яких визначено дії додавання і множення на число, утворює n-вимірний векторний простір Vn. Елементами заданого таким чином простору будуть впорядковані системи чисел, які називатимемо n-вимірними векторами і записуватимемо: Додавання двох векторів за правилом:
Множення вектора на число a,
Означення 2. Два вектори Роль нуля відіграє
Означення 3.Вектор Означення 4. Система векторів
Означення 5. Система векторів
Постає запитання: а чи існують взагалі системи лінійно незалежних векторів? Розглянемо систему векторів в n-вимірному просторі Vn:
яку далі називатимемо одиничною системою векторів. Покажемо, що така система векторів лінійно незалежна. Для цього утворимо лінійну комбінацію: Згодом побачимо, що у просторі Vn існує безліч лінійно незалежних систем векторів. Сформулюємо таке важливе твердження. Будь-яка система векторів, що складається з більшої кількості векторів, ніж розмірність простору Vn, буде лінійно залежною. Означення 6. Лінійно незалежна система n-вимірних векторів З розглянутого твердження випливає, що в n-вимірному просторі кожна лінійно незалежна система, яка складається з n векторів, буде максимальною, а також будь-яка максимальна, лінійно незалежна система векторів у цьому просторі складається з n векторів. Означення 7. Базисом векторного простору Vn називається будь-яка максимальна (повна) лінійно незалежна система векторів цього простору. Так, систему векторів:
можна розглядати як базис простору V3. Розглянемо дві системи векторів:
Система векторів (1.3) лінійно виражається через систему векторів (1.2), якщо кожний із них є лінійною комбінацією системи (1.2), тобто Означення 8. Дві системи векторів називаються еквівалентними, якщо кожна з них виражається лінійно через іншу. Означення 9. Кількість векторів, що входять до будь-якої максимальної лінійно незалежної підсистеми даної системи векторів, називається рангом цієї системи. Ранг системи векторів має відповідний зв’язок з рангом матриці. Якщо, наприклад, із компонентів векторів системи (1.2) утворити матрицю 2. Зв’язок між базисами Простір Vn має базис:
Якщо взяти довільний вектор
де хоча б одне з aі відмінне від нуля. Отже, вектор Нехай у просторі Vn задано два базиси:
Кожен вектор нового базису (1.7) однозначно можна аналогічно (1.5) подати через базис (1.6) у вигляді
Означення 9. Матрицю Якщо розглянути дві матриці е і
Водночас, якщо
Скориставшись (1.9) і (1.10), запишемо:
З останньої рівності випливає, що матриця переходу від одного базису до іншого завжди є невиродженою матрицею, а кількість базисів у Vn дорівнює кількості невироджених квадратних матриць. Якщо є два базиси, то матриці переходу від одного до іншого взаємно обернені. Нехай в Vn задано два базиси (1.6) і (1.7) з матрицею переходу
Помноживши рівність (1.11) зліва на матрицю
звідки можна визначити координати вектора в новому базисі Лінійні перетворення Нехай задано векторний простір Vn і вектори Означення 10. Перетворення 1. З означення випливає:
Нехай у просторі Vn задано деякий базис:
Будь-який вектор
З координат векторів
Матриця А задає лінійне перетворення j у базисі (1.13). Якщо через Нехай маємо базиси
і нехай лінійне перетворення j задається в цих базисах відповідно матрицями А і А¢.
Остання рівність (1.17) з урахуванням (1.18) записується у вигляді Зауважимо, що квадратні матриці В і С називаються подібними, якщо вони пов’язані рівністю Таким чином, матриці, що задають одне й те саме лінійне перетворення в різних базисах, подібні між собою. Нехай у просторі
Добутком Легко показати, що перетворення Нехай у базисі Тоді для векторів базису маємо:
Отже, можна стверджувати, що матриця суми і добутку лінійних перетворень дорівнює відповідно сумі і добутку матриць цих перетворень в одному й тому самому базисі. А операції з лінійними перетвореннями мають ті самі властивості, що й операції з матрицями. Власні числа і власні вектори матриці Нехай
Поліном n-го степеня Можна стверджувати, що подібні матриці мають однакові характеристичні поліноми і, як наслідок, однакові власні числа. Наслідок. Лінійне перетворення j в різних базисах має різні матриці, але всі вони мають однакові власні числа. Тому можна стверджувати, що лінійне перетворення j характеризується набором власних чисел, які далі називатимемо спектром лінійного перетворення j, або спектром матриці А. Розглянемо лінійне перетворення j у просторі Vn, таке що переводить відмінний від нуля вектор
Такий вектор Розглянемо тепер задачу відшукання такого базису для лінійного перетворення j, в якому б його матриця мала найпростіший діагональний вигляд. Вважатимемо, що лінійне перетворення j має такий характеристичний поліном, що всі його корені дійсні і різні. Тобто, розв’язавши рівняння n-го порядку Кожному власному числу lі відповідає певний власний вектор. Власних векторів у цьому разі буде також n. Вони утворюють лінійно незалежну систему векторів. Їх можна розглядати як базис Vn, в якому матриця лінійного перетворення A набирає найпростішого діагонального вигляду.
Поиск по сайту: |
 . Числа ai, i = 1, 2, 3, ..., n називаються компонентами вектора
. Числа ai, i = 1, 2, 3, ..., n називаються компонентами вектора  . Якщо розглянути ще один елемент простору Vn — вектор
. Якщо розглянути ще один елемент простору Vn — вектор 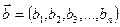 , то у просторі Vn можна виконувати такі дії.
, то у просторі Vn можна виконувати такі дії.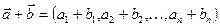 .
. за правилом:
за правилом: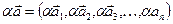 .
. вважаються рівними, якщо виконуються рівності
вважаються рівними, якщо виконуються рівності 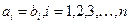 .
. . З означень дій додавання і множення вектора на число випливають властивості:
. З означень дій додавання і множення вектора на число випливають властивості: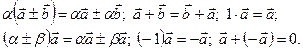
 називається лінійною комбінацією векторів
називається лінійною комбінацією векторів 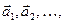
 , якщо існують такі числа
, якщо існують такі числа 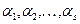 , що
, що 
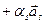 .
. називається лінійно залежною, якщо існують такі числа
називається лінійно залежною, якщо існують такі числа  хоча б одне з яких відмінне від нуля, що виконується рівність
хоча б одне з яких відмінне від нуля, що виконується рівність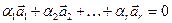 . (1.1)
. (1.1)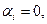
 , що виконується рівність
, що виконується рівність
 . Ліва частина цієї рівності є вектор
. Ліва частина цієї рівності є вектор 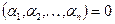 . Звідси випливає, що всі
. Звідси випливає, що всі 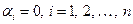 .
. називається максимальною, або повною, лінійно незалежною системою, якщо в результаті додавання до неї будь-якого відмінного від
називається максимальною, або повною, лінійно незалежною системою, якщо в результаті додавання до неї будь-якого відмінного від 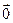 n-вимірного вектора
n-вимірного вектора 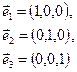
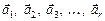 , (1.2)
, (1.2) . (1.3)
. (1.3)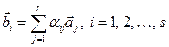 .
.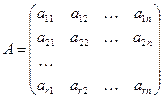 , то її ранг дорівнюватиме рангу системи векторів і вказуватиме на максимальну кількість лінійно незалежних векторів-рядків (стовпців) цієї матриці. Отже, з рангом можна пов’язати і максимальну кількість лінійно незалежних рівнянь у системі лінійних рівнянь.
, то її ранг дорівнюватиме рангу системи векторів і вказуватиме на максимальну кількість лінійно незалежних векторів-рядків (стовпців) цієї матриці. Отже, з рангом можна пов’язати і максимальну кількість лінійно незалежних рівнянь у системі лінійних рівнянь. . (1.4)
. (1.4) , то з максимальності лінійно незалежної системи векторів (1.4) випливає, що
, то з максимальності лінійно незалежної системи векторів (1.4) випливає, що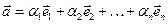 , (1.5)
, (1.5)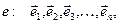 (1.6)
(1.6)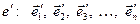 . (1.7)
. (1.7) (1.8)
(1.8) , стовпцями якої є координати векторів нового базису (1.7) у старому базисі (1.6), називатимемо матрицею переходу від базису е до базису
, стовпцями якої є координати векторів нового базису (1.7) у старому базисі (1.6), називатимемо матрицею переходу від базису е до базису  .
. базисів, то рівність (1.8) можна записати в матричному вигляді:
базисів, то рівність (1.8) можна записати в матричному вигляді: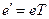 . (1.9)
. (1.9) — матриця переходу від базису (1.6) до базису (1.9), маємо рівність:
— матриця переходу від базису (1.6) до базису (1.9), маємо рівність: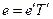 . (1.10)
. (1.10) .
. . Зв’язок між координатами довільного вектора
. Зв’язок між координатами довільного вектора 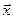 у цих двох базисах подається формулою:
у цих двох базисах подається формулою: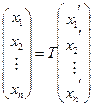 . (1.11)
. (1.11) , дістанемо:
, дістанемо: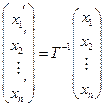 , (1.12)
, (1.12)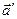 — деякі елементи цього простору.
— деякі елементи цього простору.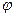 , яке переводить кожен вектор
, яке переводить кожен вектор  у деякий вектор
у деякий вектор 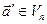 , такий що
, такий що 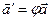 , де вектор
, де вектор  . 2.
. 2.  .
.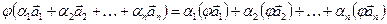 .
. . (1.13)
. (1.13) у базисі (1.13) однозначно задається співвідношенням
у базисі (1.13) однозначно задається співвідношенням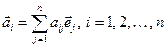 . (1.14)
. (1.14) , записавши координати векторів
, записавши координати векторів  . (1.15)
. (1.15)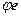 позначимо рядок, складений з векторів бази, то з (1.14) і (1.15) випливає матрична рівність між лінійним перетворенням j і матрицею А в базисі е:
позначимо рядок, складений з векторів бази, то з (1.14) і (1.15) випливає матрична рівність між лінійним перетворенням j і матрицею А в базисі е:  . Знаючи матрицю А лінійного перетворення j в базисі (1.13), можна за координатами вектора
. Знаючи матрицю А лінійного перетворення j в базисі (1.13), можна за координатами вектора  за формулою
за формулою  , якщо
, якщо  . Стовпець координат вектора
. Стовпець координат вектора  (образу) дорівнює матриці А лінійного перетворення j, помноженій справа на стовпець координат вектора
(образу) дорівнює матриці А лінійного перетворення j, помноженій справа на стовпець координат вектора 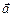 . Якщо порівняти останню рівність з рівністю (1.12), очевидна повна їх аналогія, причому матриця Т була невиродженою.
. Якщо порівняти останню рівність з рівністю (1.12), очевидна повна їх аналогія, причому матриця Т була невиродженою. і
і 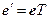 , (1.16)
, (1.16)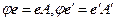 . (1.17)
. (1.17) . А проте
. А проте  . Тому, прирівнюючи праві частини, маємо:
. Тому, прирівнюючи праві частини, маємо: 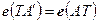 . Звідси на підставі лінійної незалежності базису і єдиності розкладу за базисом випливає:
. Звідси на підставі лінійної незалежності базису і єдиності розкладу за базисом випливає:  . Матриця Т невироджена. Отже, існує Т–1 і остаточно дістанемо співвідношення
. Матриця Т невироджена. Отже, існує Т–1 і остаточно дістанемо співвідношення 
 .
. , де Q — деяка невироджена квадратна матриця.
, де Q — деяка невироджена квадратна матриця. задано лінійні перетворення
задано лінійні перетворення  Назвемо сумою цих перетворень перетворення
Назвемо сумою цих перетворень перетворення 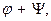 якщо
якщо
 назвемо перетворення, для якого виконується рівність
назвемо перетворення, для якого виконується рівність  Нарешті, добутком лінійного перетворення φ на число
Нарешті, добутком лінійного перетворення φ на число 
 є лінійними.
є лінійними.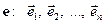 перетворення
перетворення  задаються відповідно матрицями
задаються відповідно матрицями 
 , тобто
, тобто 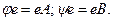

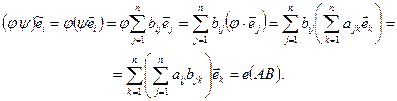
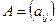 — деяка квадратна матриця розміру
— деяка квадратна матриця розміру  з дійсними елементами,
з дійсними елементами,  — деяке невідоме число. Тоді матриця
— деяке невідоме число. Тоді матриця  , де Е — одинична матриця, називається характеристичною матрицею для матриці А:
, де Е — одинична матриця, називається характеристичною матрицею для матриці А: .
.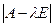 називається характеристичним поліномом матриці А, а його корені – власними числами матриці А.
називається характеристичним поліномом матриці А, а його корені – власними числами матриці А. у вектор, пропорційний до самого вектора
у вектор, пропорційний до самого вектора 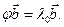 (1.19)
(1.19)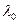 — власним числом, що відповідає цьому власному вектору.
— власним числом, що відповідає цьому власному вектору.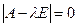 , знайдемо n різних дійсних коренів
, знайдемо n різних дійсних коренів 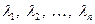 . Якщо виконується така умова, то лінійне перетворення j дійсного лінійного простору Vn має простий спектр.
. Якщо виконується така умова, то лінійне перетворення j дійсного лінійного простору Vn має простий спектр.