 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел функции. Непрерывность функции. Точки разрыва
1.3.10. Среди графиков, приведенных на рис., указать ВСЕ, соответствующие формуле
1.3.11. Среди графиков, приведенных на рис., указать ВСЕ, соответствующие формуле
1.3.13. Указать ВСЕ утверждения, справедливые для графика функции, изображенного на рис. … (выберите несколько вариантов ответа)
1) 4)
1.3.14. Если 1) 5 2) – 5 3) 0 4)
1.3.15. Если 1) 1 2) – 1 3) 0 4)
1.3.16. Если 1) 1 2) – 1 3) 0 4)
1.3.17. Если 1) 3 2) – 3 3) 0 4) 1.3.18. Вычислить 1) 1 2) – 1 3) 0 4) 1.3.19. Вычислить 1) 1 2) – 1 3) 0 4)
1.3.20. Вычислить 1) 1 2) – 1 3) 0 4) 1.3.21. Среди перечисленных вариантов ответа выбрать значение предела 1) 1.3.22. Среди перечисленных вариантов ответа выбрать значение предела 1) 1.3.23.Среди перечисленных вариантов ответа выбрать значение предела 1) 1.3.24. Среди перечисленных вариантов ответа выбрать значение предела 1) 1.3.25.Среди перечисленных вариантов ответа выбрать значение предела 1) 1.3.26.Среди перечисленных вариантов ответов выбрать значение предела 1)
1.3.27. Найти предел функции 1) 2 2) 1 3) -1 4) другой ответ
1.3.28. Найти предел функции 1) 4 2) 6 3) 1.3.29.Найти предел 1) 1/2 2) 1/4 3) 1/5 4) 5/6 1.3.30. Среди перечисленных вариантов ответов выбрать значение предела 1)
1.3.31. Среди перечисленных вариантов ответов выбрать значение предела 1)
1.3.32. Среди перечисленных вариантов ответов выбрать значение предела 1) 1.3.33. Среди перечисленных вариантов ответов выбрать значение предела 1) 1.3.34. Среди перечисленных вариантов ответов выбрать значение предела 1) 1.3.35.Среди перечисленных вариантов ответов выбрать значение предела 1) 1.3.36. Среди перечисленных вариантов ответов выбрать значение предела 1) 1 2) 0 3) 1.3.37.Среди перечисленных вариантов ответов выбрать значение предела 1) 1.3.38. Для функции 1) точкой непрерывности 2) точкой устранимого разрыва 2) точкой разрыва первого рода (скачка) 4) точкой разрыва второго рода (бесконечного)
1.3.39. Для функции 1) точкой непрерывности 2) точкой устранимого разрыва 2) точкой разрыва первого рода (скачка) 4) точкой разрыва второго рода (бесконечного)
1.3.40. Для функции 1) точкой непрерывности 2) точкой устранимого разрыва 3) точкой разрыва первого рода (скачка) 3) точкой разрыва второго рода (бесконечного)
1.3.41. Для функции 1) точкой непрерывности 2) точкой устранимого разрыва 3) точкой разрыва первого рода (скачка) 4) точкой разрыва второго рода (бесконечного)
1.3.42.Для функции 1) точкой непрерывности 2) точкой устранимого разрыва 3) точкой разрыва первого рода (скачка) 4) точкой разрыва второго рода (бесконечного)
1.3.43. Для функции 1) точкой непрерывности 2) точкой устранимого разрыва 3) точкой разрыва первого рода (скачка) 4) точкой разрыва второго рода (бесконечного)
1.3.44. Среди графиков, приведенных на рис., укажите ВСЕ, на которых функция имеет в точке а разрыв второго рода.
1.3.45. Среди графиков, приведенных на рис., укажите ВСЕ, на которых функция имеет в точке «а» разрыв первого рода.
1.3.46. Среди графиков, приведенных на рис., укажите ВСЕ, на которых функция непрерывна в точке «а»:
1.3.47. Известно, что 1) с – точка разрыва первого рода 2) с – точка устранимого разрыва 3) с –точка разрыва второго рода 4) с – точка непрерывности
1.3.48. Известно, что 1) с – точка разрыва первого рода 2) с – точка устранимого разрыва 3) с –точка разрыва второго рода 4) с – точка непрерывности
1.3.49. Укажите, в каком случае в точке «с» функция f(x) имеет устранимый разрыв: 1) 3)
1.3.50.Известно, что f(x) – непрерывная функция. Какое из следующих утверждений верно? 1) 3)
1.3.51. Функция f(x) имеет устранимый разрыв в точке х = 2 и 1) 1 2) –1 3) 0 4) ¥ 5) другой ответ.
1.3.52. Известно, что f(x) и g(x) – непрерывны в точке х = 1; f(1) ¹ 0; g(1) = 0. Укажите ВСЕ функции непрерывные в точке х = 1: 1) f(x)+g(x) 2)
1.3.53. Укажите ВСЕ функции непрерывные в точке х = 1: 1) 1.3.54. Укажите правильное продолжение фразы: "В точке х=2 функция 1) имеет разрыв 1-го рода; 2) имеет разрыв 2-го рода; 3) имеет устранимый разрыв; 4) непрерывна 1.3.55. Известно, что при 1) 2) 3) 4)
1.3.56. Известно, что при 1) 2) 3) 4)
1.3.57. При 1)
Поиск по сайту: |
 … (выберите несколько вариантов ответа)
… (выберите несколько вариантов ответа)
 … (выберите несколько вариантов ответа)
… (выберите несколько вариантов ответа) … (выберите несколько вариантов ответа)
… (выберите несколько вариантов ответа)

 5)
5)  6)
6) 
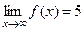 , то
, то  равен …
равен … 5) не существует
5) не существует , то
, то  равен …
равен … , то
, то  и f(x) – четная, то
и f(x) – четная, то  равен …
равен …

 :
:
 2)
2)  3) 1/3 4) 0
3) 1/3 4) 0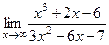 :
: :
: :
: :
: 2)
2)  :
: :
: :
:
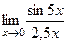 :
: :
: :
: :
: 2)
2)  3)
3)  4)
4) 
 :
: :
: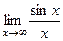 :
: :
: 2)
2)  3) 1/4 4) 3/4
3) 1/4 4) 3/4 точка
точка 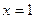 является:
является: точка
точка  точка
точка  является:
является: точка
точка  является:
является: точка
точка  точка
точка 
 . Какое из утверждений верно?
. Какое из утверждений верно? ; f(c) = – 5. Какое из утверждений верно?
; f(c) = – 5. Какое из утверждений верно? f(c) = 5;
f(c) = 5; 4)
4)  2)
2) 
 4)
4) 
 . Тогда
. Тогда  равен
равен 3) f(x).g(x) 4)
3) f(x).g(x) 4)  5)
5) 
 2)
2)  3)
3)  4)
4)  5)
5) 
 …
…
 и
и  – бесконечно малые и
– бесконечно малые и  . Какое из следующих утверждений верно при
. Какое из следующих утверждений верно при  бесконечно малые
бесконечно малые  укажите ВСЕ верные утверждения:
укажите ВСЕ верные утверждения: ~
~  2)
2)  3)
3)  ~
~  4)
4) 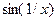 ~
~ 