 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Розрахунок на міцність дерев’яної консольної балки
Розрахунково-графічна робота “Дослідження геометричних характеристик перерізів та розрахунок балок на міцність” Зміст роботи Задача №1 Дослідження геометричних характеристик складного перерізу Для заданого плоского поперечного перерізу, що складається з декількох елементів, визначити основні геометричні характеристики. При дослідженні геометричних характеристик складного перерізу потрібно: 1. Визначити положення центру перерізу відносно допоміжних осей. 2. Обчислити осьові моменти інерції відносно головних центральних осей. 3. Визначити моменти опору перерізу при згині та радіуси інерції. Задача №2 Розрахунок на міцність однопрольотної сталевої двотаврової балки на шарнірних опорах Для однопрольотної сталевої шарнірно обіпертої балки побудувати епюри Q і M аналітичним методом та визначити з умови міцності за нормальними напруженнями номер стандартного прокатного двотаврового профілю при [ ϭ ] = 160 МПа. При розв’язуванні задачі потрібно: 1. Визначити реакції опор аналітичним методом і виконати перевірку визначення реакцій. 2. Скласти рівняння реакцій поперечних сил Q(z) і згинальних моментів M(z) для кожної ділянки балки та побудувати відповідні епюри. 3. Підібрати номер двотаврового профілю, який забезпечує міцність балки. Задача №3 Розрахунок на міцність дерев’яної консольної балки Для консольної клеєної дерев’яної балки прямокутного перерізу із заданим співвідношенням h/b побудувати епюри Q і M, визначити розміри перерізу з умови міцності за нормальними напруженнями при [ ϭ ] = 14 МПа та виконати перевірку міцності за дотичними напруженнями при [ τ ] = 2 МПа. При розв’язуванні задачі потрібно: 1. Скласти рівняння Q(z) і M(z) для кожної ділянки балки і побудувати епюри. 2. Підібрати розміри прямокутного перерізу при заданому співвідношенні h/b. 3. Виконати перевірку міцності за дотичними напруженнями.
Задача №1 Дослідження геометричних характеристик складного перерізу Хід виконання задачі №1 показаний на прикладі визначення геометричних характеристик перерізу, що складається з трьох елементів: швелера №16 і двотавра №20,20. 1. Заданий складний переріз викреслюється на форматі А4 в певному масштабі (ДСТУ ISO 128-50:2005). На креслення наносяться центральні осі кожного з складових елементів – швелера, двотавра, відповідно x1y1, x2y2, x3y3 з центрами c1, c2, c3. 2. Проводиться допоміжна вісь Y0 паралельно осям Y1, Y2, і Y3 для визначення положення центра складного перерізу і центральної осі Y. Другу допоміжну вісь обирати непотрібно, тому що положення центральної осі y відомо – це вісь симетрії перерізу. 3. З таблиць сортаментів прокатної сталі виписуються необхідні дані для швелера і двотавра.
4. Визначаються координати центрів c1, c2 і c3 складових елементів перерізу вілносно допоміжної осі X0. Y1 = 0,5 * b1 = 0,5 * 1 = 0,5см Y2 = b1 + b2 – z0 2= 1+ 5,8 – 1,62 = 5,18см Y3 = b1 + b2 + 0,5 * h3 = 1 + 5,8 + 0,5 * 16 = 14,8см 5. Обчислюється координата центру складного перерізу: Yc = 6. Проводиться центральна вісь X через центр С складного перерізу паралельно допоміжній осі X0. 7. Визначаються величини осьових моментів інерції складного перерізу.
α1 = Х1 – Х0 = 0,5 – 7,18 = - 6,68см
b1 = 1 см
a2 = x2 – x0 = 5,18 – 7,18 = -2 см
b2 = 5,8 см
a3 = X3 – X0 = 14,8 – 7,18 = 7,62см
b3 = 8,1
IX = IY = 8. Визначаємо величини моментів опору перерізів. Wx =
Wy = Xmax = 9. Визначаються величини головних радіусів інерції перерізу: τx = τy =
Задача №2 Розрахунок на міцність однопрольотної сталевої двотаврової балки на шарнірних опорах 1. Для заданої схеми балки визначаються реакції опор. Складаються рівняння рівноваги: ∑ MA = 0; - q * 10 * 5 + M – F * 7 + RB * 10 = 0 RB * 10 = 250 – 70 + 7 = 0 RB = ∑ MB= 0; F - 3 + M + q * 10 * 5 – RA * 10 = 0 – RA * 10 = - 30 + 70 * 250 = 0 RA = Перевірка ∑Y = 0 RA – F – q * 10 + RB = 25 – 10 – 50 + 35 = 0 2. Складаються рівняння Q(z) і M(z). Ділянка 1 0 ≤ z1 ≤ 5 Q(z1) = RA – q*z1 Q(0) = 36кН Q(5) = 35-5*5=10кН M(z1) = RA * z1 – q*z1* M(0) = 35 * 0 – 5*0 M(5) = 35 * 5*5
Ділянка 2 5 ≤ z2 ≤ 7 Q(z2) = RA – q * Z2 Q(5) = 35 – 5 * 5 =10 кН Q(7) = 35 - 5 * 7 = 0 кН M(z2) = RA * Z2 – M – q* Z2 M(5) = 35 * 5 – 70 – 5 * 5 M(7) = 35 * 7 – 70 – 5 * 7
Ділянка 3 0 ≤ z3 ≤ 3 Q(z3) = - RB +q * z3 Q(0) = - 25 + 5 * 0 = - 25 кН Q(3) = - 25+5 * 3 = - 10 кН M(z3) = RB * z3 – q * z3 * M(0) = 25 * 0 = 0 кН/м M(3) = 25 * 3-5*3 = 52,5 кН/м За даними підрахунків будуються епюри Q(z) і M(z). 3. Підбирається необхідний номер двотавра з умови міцності. Небезпечним є переріз, де виникає найбільший за величиною момент Mmax = 160кН/м. ϭmax = Wx = За таблицями сортаменту обираэмо двотавр: № 36; Wx = 743см3 № 40; Wx = 953см3 Визначаємо нормальні напруження для двотавра № 36: ϭmax = Міцність балки забезпечена.
Задача №3 Розрахунок на міцність дерев’яної консольної балки 1. Складаємо рівняння Q(z) і M(z). При цьому початок координат обирається у вільному кінці консолі, що позбавляє від необхідності визначення реакцій опори. Переріз (1-1) 0 ≤ z1 ≤ 2 Q(z1) = F Q(0) =10кН Q(2) = 10кН M(z1) = F * z1 M(0) = 10 * 0 = 0кН/м M(2) = 10 * 2 = 20кН/м
Переріз (2-2) 2 ≤ z2 ≤ 6 Q(z2) = F – q *(z2 – 2) Q(2) = 10 - 4 * (2 - 2) = 10 кН Q(6) = 10 - 4 * (6 – 2) = - 6кН M(z2) = F * z2 – q * (z2 - 2)* M(2) = 10 * 2 – 4 * (2 - 2)* M(6) = F * 6 – 4 * (6 - 2)* M(4,5) = 10 * 4,5 – 4 * (4,5 - 2)* F - q * (Z0 - 2) 10 =4 * (Z0 - 2) Z0 – 2 = 10/4 = 2,5 Z0 = 2 + 2,5 = 4,5
Переріз (3-3) 6 ≤ z3 ≤ 8 Q(z3) = F – q *4 Q(6) = 10 - 4 * 4 = - 6кН Q(8) = 10 - 4 * 4 = - 6кН M(z3) = F * z3 – M * q * 4 * (z3 - 4 ) M(7) = 10 * 6 – 25 * 4 * 4 * (6 - 4 ) = 3кН/м M(8) = F * 8 – 25 * 4 * 4 * (8 - 4 ) = - 9кН/м
2. Підбирається необхідний з умови міцності прямокутний переріз. Небезпечним є переріз, де виникає найбільший за величиною згинальний момент Mmax = 12кН/м. Wx = Визначаємо геометричні розміри прямокутного дерев’яного перерізу балки. Wx = при
h3 = 7,2 * 1333,3 h = Приймаємо h = 21см b = Приймаємо b = 18см Визначаємо дійсний момент опору: Wx = Перевіряється виконання умови міцності: ϭmax = ∆δ = Міцність балки за нормальними напруженнями забезпечена. Отже приймаємо остаточно: h = 21см, b = 18см 3. Перевірка на міцність за дотичними напруженнями. Небезпечним є переріз, де виникає найбільша за величиною поперечна сила Qmax = 10кН. τmax = Міцність за дотичними напруженнями забезпечена.
Поиск по сайту: |
 =
=  = 63,6см4
= 63,6см4
 =
=  = 58,6см4
= 58,6см4
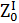 = 1,8см
= 1,8см
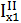 = 49,1см4
= 49,1см4
 =
=  = 873см4
= 873см4
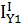 =
=  = 747см4
= 747см4
 = 45,4см4
= 45,4см4
 =
=  = 7,18см
= 7,18см =
=  * A1 =486+(-6,68)2 *18=1289,2см4
* A1 =486+(-6,68)2 *18=1289,2см4 =
= 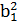 * A1 = 1,5 + 12 * 18 = 19,5см4
* A1 = 1,5 + 12 * 18 = 19,5см4 =
=  +
+  * A2 = 491 + (-2)2 *16,6 = 557,4см4
* A2 = 491 + (-2)2 *16,6 = 557,4см4 =
=  * A2 = 45,4 + 5,82 * 16,6 = 603,8см4
* A2 = 45,4 + 5,82 * 16,6 = 603,8см4 =
=  +
+ 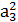 * A3 =5,86 + 7,622 * 20,2 = 1231,5см4
* A3 =5,86 + 7,622 * 20,2 = 1231,5см4 =
=  +
+ 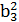 * A3 = 873 + 8,1 * 20,2 = 2198,3см4
* A3 = 873 + 8,1 * 20,2 = 2198,3см4 +
+  = 19,5 + 603,8 + 2198,3 = 2821,6см4
= 19,5 + 603,8 + 2198,3 = 2821,6см4 =
= 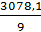 = 342см3
= 342см3 = Yc = 18,13см
= Yc = 18,13см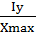 =
= 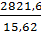 = 180,6см3
= 180,6см3 h2 = 10см
h2 = 10см =
= 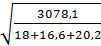 =
=  = 7,49см
= 7,49см =
=  =
=  = 7,17см
= 7,17см = 25кН
= 25кН = 35кН
= 35кН
 = 0 кН/м
= 0 кН/м = 112,5 кН/м
= 112,5 кН/м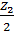
 = 42,5 кН/м
= 42,5 кН/м = 52,5 кН/м
= 52,5 кН/м
 = [ ϭ ]
= [ ϭ ] =
= 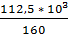 = 765,6см3
= 765,6см3 = 151,4МПа < [ ϭ ] = 160МПа
= 151,4МПа < [ ϭ ] = 160МПа - M
- M - 25 = - 5кН/м
- 25 = - 5кН/м - 25 = 3кН/м
- 25 = 3кН/м - 25 = 3кН/м
- 25 = 3кН/м = 1333,3см3
= 1333,3см3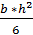 =
=  =
= 
 = 1,2 => b =
= 1,2 => b = 
 = (9599,8)0,3333333 = 21,3см
= (9599,8)0,3333333 = 21,3см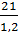 = 17,8см
= 17,8см = 1323см3
= 1323см3 = 15,1МПа > [ ϭ ] = 15МПа
= 15,1МПа > [ ϭ ] = 15МПа * 100 =
* 100 =  * 100 = 0,6 % <[ 5 %]
* 100 = 0,6 % <[ 5 %] *
*  =
=  = 0,48МПа ≤ [ τ ] = 2МПа
= 0,48МПа ≤ [ τ ] = 2МПа