 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства средней арифметической
Тема 6: Средние величины В зависимости от особенностей распределения рассчитывают показатели, которые возможно разделить на три основные группы: 1) уровень изучаемого признака; 2) вариация изучаемого признака; 3) форма распределения. Важнейшей характеристикой уровня изучаемого признака является средняя величина. Взаимодействие элементов совокупности приводит к ограничению вариации хотя бы части их свойств
Средняя величина-
Средние величины бывают:
Пример: средняя величина надоя молока от коров черно-пестрой породы на первом году лактации при норме кормления 12,5 кормовой единицы в сутки.
Пример: средняя скорость гоночных автомобилей
Общая и групповые средние Средняя величина, рассчитанная по совокупности в целом, называется общей средней.Она дополняется средними, если совокупность разделить на отдельные группы. Такие средние величины называются групповыми средними. Виды средних величин
Если совокупность разбита на несколько групп и в каждой группе рассчитана своя средняя арифметическая величина
Степенные средние величины:
Многие виды средних могут быть получены из формулы степенной средней. Подставив в её формулу значение Z (показатель степени), определяемое объектом и задачами исследования, возможно получить тот или иной вид средней: арифметическую, гармоническую, геометрическую, квадратическую и т.д. Виды степенных средних величин
Здесь
Свойства средней арифметической 1) сумма отклонений отдельных значений признака от средней арифметической равна нулю; 2) если от каждого значения признака вычесть или к каждому его значению прибавить одно и то же число, то средняя соответственно уменьшится или увеличится на то же самое число; 3) если каждое значение признака разделить или умножить на одно и то же число, то средняя соответственно уменьшится или увеличится во столько же раз; 4) если значения признака-веса разделить или умножить на одно и то же число, то величина средней не изменится; 5) сумма квадратов отклонений значений признака от средней меньше суммы квадратов отклонений от любой произвольной величины; 6) произведение средней на сумму частот всегда равно сумме произведений вариантов на частоты.
Поиск по сайту: |
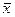 - обобщающая величина изучаемого признака в совокупности, которая характеризует либо типичный уровень по качественно однородной совокупности, либо совокупность в целом.
- обобщающая величина изучаемого признака в совокупности, которая характеризует либо типичный уровень по качественно однородной совокупности, либо совокупность в целом.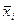 , общая средняя для всей совокупности составит:
, общая средняя для всей совокупности составит: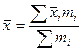
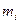 - объем i-й группы.
- объем i-й группы.
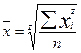


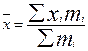

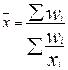




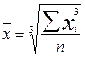

 - значения изучаемого признака, n - объем совокупности,
- значения изучаемого признака, n - объем совокупности, 