 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Показатели концентрации
Показатели дифференциации Порядковые (ранговые) характеристики распределения: Квартили – значения признака, которые делят ранжированный ряд на четыре равные по численности части. Квартильное отклонение: где Децили D – это значения вариантов, которые делят упорядоченный ряд по объему на 10 равных частей. Следовательно, в ряду распределения выделяют 9 децилей.
Группировка банков по величине полученной прибыли
Знак (-) означает, что значение признака, совпадающее с верхней границей интервала в этот интервал не включается, а попадает в следующий. Квартили: - определение места квартилей:
- расчет квартилей:
- расчет квартильного отклонения:
- расчет коэффициента квартильной вариации:
1. Децили: – определение места децилей:
- расчет децилей:
- расчет коэффициента децильной дифференциации: КD = D9 – девятая дециль D1 - первая дециль Он показывает, во сколько раз прибыль 10% банков с самыми высокими значениями прибыли превышают прибыль 10% банков с самыми низкими значениями прибыли. Коэффициент фондовой дифференциации: Кф = где
Показатели концентрации - коэффициент концентрации Джини (от 0 до 1): G = где !!!
Вспомогательная таблица для расчета к-та Джини
G = В статистической практике к-т Джини используется для характеристики степени неравномерности распределения населения по уровню доходов. - коэффициент Герфиндаляиспользуют для оценки концентрации производства. Он вычисляется на основе данных о доле производства или доходов отдельных групп в совокупном объеме производства или доходов: H = где !!!
Значение к-та Герфиндаля (Н) определяется влиянием лишь доминирующих групп и зависит от числа единиц совокупности в группах. - коэффициент Лоренца (L) характеризует концентрацию, степень неравномерности распределения доходов путем сравнения долей численности единиц в группах ( L = yi
100 pi Кривые распределения Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения. Особенности кривой нормального распределения таковы: 1. Кривая симметрична и имеет максимум в точке, соответствующей значению
2. Кривая имеет две точки перегиба, находящиеся на расстоянии ± σ от 3. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности; чем больше значения отклонений от 4. При 5.Коэффициенты асимметрии и эксцесса равны нулю. 6. Площадь между ординатами, проведенными на расстоянии: ü ü ü ± 3 σ составляет 99,7% всех значений признака. Как определить соответствие полученного распределения признака в исследуемой совокупности нормальному распределению? Для решения этого вопроса следует рассчитать теоретические частоты нормального распределения, т.е. те частоты, которые имели бы место, если бы данное распределение в точности следовало закону нормального распределения. Для расчета теоретических частот применяется формула:
Величина
Порядок расчета теоретических частот кривой нормального распределения: 1. По эмпирическим данным рассчитываются 2. Находят нормированное отклонение каждого варианта от t = 3. По таблице распределения функции 4. Вычисляют теоретические частоты для каждого интервала по формуле:
Пример: Рассчитать теоретические частоты ряда распределения на основе данных об объемах выданных кредитов КБ региона:
1.
2. t =
Поиск по сайту: |

 и
и  – соответственно третья и первая квартили распределения.
– соответственно третья и первая квартили распределения. ;
;
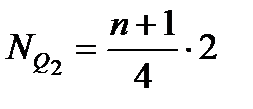 ;
;


 - нижняя граница интервала, в котором находится квартиль;
- нижняя граница интервала, в котором находится квартиль;
 - накопленная частота интервала, предшествующая тому, в которой находится квартиль;
- накопленная частота интервала, предшествующая тому, в которой находится квартиль;
 частота интервала, в котором находится квартиль.
частота интервала, в котором находится квартиль.
 ND2 =
ND2 =  ND9 =
ND9 = 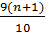
 +
+ 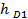 *
* 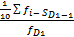 D9 = X
D9 = X  +
+ 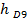 *
*  XDi - нижняя граница интервала, в котором находится дециль;
XDi - нижняя граница интервала, в котором находится дециль;
 - накопленная частота интервала, предшествующая тому, в которой находится дециль;
- накопленная частота интервала, предшествующая тому, в которой находится дециль;
 -частота интервала, в котором находится дециль.
-частота интервала, в котором находится дециль.
 = ; → интервал
= ; → интервал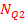 =
= 

 = ; → интервал
= ; → интервал = млрд.руб.
= млрд.руб. = млрд. руб.
= млрд. руб. млрд. руб.
млрд. руб. =
= =
=



 =
=
 . – средний уровень признака из 10% наибольших значений признака;
. – средний уровень признака из 10% наибольших значений признака; . - средний уровень признака из 10% наименьших значений признака.
. - средний уровень признака из 10% наименьших значений признака. наим. =
наим. = 

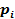 - накопленная доля (частость) численности единиц совокупности
- накопленная доля (частость) численности единиц совокупности – накопленная доля прибыли, приходящаяся на все единицы совокупности, с прибылью не более
– накопленная доля прибыли, приходящаяся на все единицы совокупности, с прибылью не более  .
.






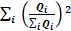
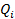 – объем производства в i- ой группе.
– объем производства в i- ой группе. ) и долей значений признака в общем объеме:
) и долей значений признака в общем объеме:

 = Mo = Me;
= Mo = Me; =
=  *
* 
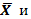

 :
: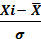
 (приложение № 1в практикуме и учебнике) определяют ее значения.
(приложение № 1в практикуме и учебнике) определяют ее значения.


 )²
)² 

 =
=  млн. руб.
млн. руб. =
=