 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Разработка методики расчета ветровых воздействий на высотные здания-комплексы, основанной на численном моделировании уравнений гидрогазодинамикиСтр 1 из 2Следующая ⇒
Численное моделирование ветровых воздействий на высотные здания и комплексы Студент 2019/1 Мусорина Т.А. Научный руководитель Петроченко О.В. Ключевые слова: комплекс зданий, ветровые нагрузки, пульсации, расчеты, обтекание, аэродинамическая труба, сила ветра, средняя и пульсационная составляющая.
За минувшие полвека изменилась не только этажность, но и внешний облик небоскребов. Так в 60-х годах широкое распространение получили высотные здания в виде гладкой стеклянной призмы, без каких-то усложнений. Постепенная застройка крупных городов небоскребами-призмами, а также прогресс в материаловедении, стимулировали поиск более сложных и неординарных архитектурных решений. В настоящее внешний облик проектируемых зданий отличают сложные геометрические формы, для которых, как правило, неизвестны значения аэродинамических коэффициентов, необходимых для определения ветровых нагрузок на несущие конструкции. [1] Сокращение свободных территорий в крупных городах приводит к необходимости строить высотные здания (по действующим нормам высотными считаются сооружение выше 75м). В связи с недавней историей высотного строительства в России и в Санкт-Петербурге многие характеристики по-прежнему не учитываются при проектировании и строительстве таких зданий. К таким характеристикам относятся ветровые нагрузки на высотные здания. Ветровые нагрузки являются одним из основных видов воздействий на конструкции зданий. Если для малоэтажных зданий ветровое давление принято считать равномерно действующим на все здание по высоте, то для высотного здания при расчете ветровых нагрузок и тепловых потерь необходимо учитывать рост скорости ветра по высоте. Повышенная высота здания определяет процесс обтекания его ветром. Режим обтекания здания воздушным потоком, помимо формы самого здания, существенно зависит от расположенных рядом других зданий и сооружений, особенностей рельефа местности. Это влияние особенно заметно, если окружающие объекты расположены на расстоянии, менее чем в пять раз превышающем высоту здания. Расчет обтекания ветровым потоком высотных зданий необходим как для определения ветровых нагрузок на конструкции здания, так и для учета влияния ветра на воздухообмен помещений. Находясь в ветровом потоке, высотное здание испытывает аэродинамические нагрузки. Существует два главных фактора, влияющих на характер аэродинамических нагрузок. Это собственная пространственно-временная структура ветра и вторичные струйно-вихревые течения.[2] Следует, по возможности, избегать сооружения однотипных высотных зданий в непосредственной близости друг от друга. При сильных ветрах и неблагоприятных направлениях воздушного потока, когда вихревые структуры, формирующиеся в следе одного здания, попадают на другое и могут возникнуть значительные аэродинамические нагрузки, приводящие к разрушению конструкций, расположенных с подветренной стороны. Основные трудности при проектировании высотных зданий состоят в том, что используемые до настоящего времени СНиП 2.01.07-85. Нагрузки и воздействия. не содержат рекомендаций по назначению аэродинамических коэффициентов для сложных по форме и крупногабаритных сооружений, в том числе для высотных зданий. [3] Для решения проблем, необходимо решить следующие задачи. Задача исследования 1. воздействия ветра на высотные зданий 2. Разработка методики расчета ветровых воздействий на высотные здания-комплексы, основанной на численном моделировании уравнений гидрогазодинамики 3. Применение данной методики на модели сооружения в аэродинамической трубе. Разработка методики расчета ветровых воздействий на высотные здания-комплексы, основанной на численном моделировании уравнений гидрогазодинамики 1. Ветровую нагрузку следует определять как сумму средней и пульсационной составляющих. Нормативное значение средней составляющей ветровой нагрузки
где k - коэффициент, учитывающий изменение ветрового давления по высоте (см. п. 6.5); с - аэродинамический коэффициент (см. п. 6.6) Нормативное значение пульсационной составляющей ветровой нагрузки
где
2. Численное моделирование ветровых воздействий на высотные здания и комплексы 1)Математическая формулировка задачи гидрогазодинамики Уравнения Навье Стокса Навье‐Стокса:
1 слагаемое- нестационарность 2 слагаемое – конвекция 3 слагаемое – градиент давлений 4 слагаемое - диффузия i, j =1, 2, 3 –оси x,y,z соответственно; p–давление; ρ–плотность (для воздуха1.18-1.40 кг/м3) μ= const –динамический коэффициент вязкости (для воздуха 1.83 10*5 м*2/c) 2) Инженерная методика оценки пиковых значений давления Разработана практическая методика оценки пиковых расчетных нагрузок на фасадные конструкции (P*max и P*min) по результатам стационарных расчетов средних давлений P, энергии турбулентных пульсаций TKE и с учетом осредненных коэффициентов обеспеченности θmax и θmin:
Где V- ”локальная” скорость, соответствующая давлению P на поверхности На предварительном этапе принимаем θmax=3.5, θmin=7 Уточнение значений:
3 Тестирование макета 3.1. Область расчета имеет следующие размеры: до входной границы расстояние 500м, до выходной границы 1200м, до боковых границ 500м. Общее число расчетных точек в сетках 1250000
Рис .1. Геометрия комплекса зданий .
Расчетные сетки используются при численном решении Уравнения Навье Стокса Навье‐Стокса. С помощью сетки можно определить координаты точек в пространстве Рис.2.схема расчетной области с многоблочной сеткой для комплекса зданий.
Рассмотрим обтекание комплекса зданий, например, при направлении ветра с севера на юг Рис. 3 направление ветра с севера на юг
Траектории меченных частиц при обтекании комплекса в направлении север-юг. Рис. 4 Траектории меченных частиц во внутреннем пространстве комплекса при направлении ветра север-юг.
Поиск по сайту: |
 на высоте z над поверхностью земли следует определять по формуле
на высоте z над поверхностью земли следует определять по формуле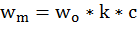
 на высоте z следует определять по формуле
на высоте z следует определять по формуле
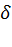 - коэффициент пульсаций давления ветра на уровне z, принимаемый по табл. 7;
- коэффициент пульсаций давления ветра на уровне z, принимаемый по табл. 7; - коэффициент пространственной корреляции пульсаций давления ветра (см. п. 6.9);[4]
- коэффициент пространственной корреляции пульсаций давления ветра (см. п. 6.9);[4] - уравнение гидрогазрдинамики
- уравнение гидрогазрдинамики


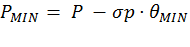
 ,
,  –стандарт давлений
–стандарт давлений
 , [2]
, [2]