 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
THE ROLE OF INFORMATION TECHNOLOGY AT THE DECISION MATRIX GAMES WITH MS EXCEL
УДК 004.8:6813.06(075.8) Лукьянова Галина Викторовна/ Lukyanova V. Galina Кандидат технических наук, доцент/ PhD in technics, associate professor Довлатян Галина Петровна/ Dovlatian P. Galina Кандидат экономических наук, доцент/ PhD in economics, associate professor Лебедева Ольга Евгеньевна/ Lebedeva E. Olga Российская Федерация, г. Шахты/ Russian Federation, Shakhty РОЛЬ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ПРИ РЕШЕНИИ МАТРИЧНЫХ ИГР C MS EXCEL THE ROLE OF INFORMATION TECHNOLOGY AT THE DECISION MATRIX GAMES WITH MS EXCEL В статье авторы применяют интерактивный метод Брауна-Робинсона для решения матричных задач с помощью информационных технологий The authors used an interactive method of Brown-Robinson for the solution of matrix problems using information technology Ключевые слова: информационные технологии, матричные игры, интерактивный метод Keywords: information technology, matrix games, interactive method В современном информационном обществе все большую роль играют информационные технологии и их управление для решения задач любой сложности. Целесообразно рассмотреть стратегически-необходимую теорию матричных игр, которая способна не только указать оптимальный путь к решению некоторых проблем, но и прогнозировать их исход. Матричные игры довольно просты, к ним могут быть сведены игры общего вида. Однако, в большинстве случаев решение представляет собой трудный и громоздкий процесс, выигрыши игроков в каждой ситуации не всегда определяются точными измерениями. В процессе сбора и анализа данных и введения при построении модели различных предположений накапливаются ошибки, точность в определении значения игры и оптимальных стратегий игроков не всегда оправдана. Погрешность в оценке игроком своего выигрыша не может привести к практически серьёзным последствиям и небольшое отклонение игрока от оптимальной стратегии не влечёт за собой существенного изменения в его выигрыше. В теории игр известны несколько способов приближенного решения матричных игр, на таких языках как: Turbo Pascal, Visual Basic, С + +. Итеративный метод Брауна-Робинсона - метод приближённого решения матричных игр реализуется в MS Excel. Идея метода – многократное фиктивное разыгрывание игры ГА с матрицей А={aij} размера (m´n). Одно разыгрывание игры - партия, число партий не ограниченно. В 1-ой партии оба игрока выбирают произвольные чистые стратегии. Игрок 1 выбрал i-ю стратегию, а игрок 2 – j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия. С ростом числа шагов смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Процесс приближённого нахождения оптимальных стратегий игроков называется итеративным, а его шаги – итерациями. За первые k разыгрываний игрок 1 использовал i-ю чистую стратегию Игрок 1 следит за действиями игрока 2 и с каждым своим ходом желает получить как можно больший выигрыш. В ответ на применение игроком 2 своей смешанной стратегии yk, он будет использовать чистую стратегию ik+1 , которая обеспечит ему лучший результат при разыгрывании (k+1)-ой партии. Игрок 2 поступает аналогично. В худшем случае каждый из них может получить:
где Соотношения, определяющие средние значения проигрыша игрока 2 и выигрыша игрока 1:
Если ν - цена матричной игры ГА. Её значение будет больше выигрыша игрока 1, но меньше проигрыша игрока 2, т. е.
Таким образом, получен итеративный процесс, позволяющий находить приближённое решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала
Сходимость алгоритма гарантируется теоремой: Лемма. Для всякой матрицы А и "e>0 существует такое k0, что При предельном переходе в неравенстве (1) при k®¥ имеем: Из леммы следует, что На основании неравенства (1) имеем: оценка для разности пределов: Итак, Приближённое решение игры с матрицей А= Шаг 1. На листе 1 создается матрица размерностью [3х3], игру начинает первый игрок (А1). Шаги в программе MS Excel выполняются автоматически согласно методу Брауна-Робинсона.
Рис.1 Шаг 2. Первый игрок произвольно выбирает одну из своих чистых стратегий. Предположим, что он выбрал свою 1-ю стратегию, а игрок 2 (В1), в результате расчетов стратегий, отвечает своей 1-й стратегией и Расчет показателей первого игрока (А1), при n=1
Рис.2 Расчет показателей второго игрока (В1), при n=1
Рис.3 Замечание: В зависимости от того, какой из игроков начнет игру первым (игрок 1- А1 или игрок 2-В1), зависит расчет показателей на Рис.3: Если игру начнет игрок А1, тогда накопленный выигрыш, противника, за первые n-шагов будет отображен в ячейках: AL14; AN14; AP14; AR14; AT14. Если игру начнет игрок В1, тогда накопленный выигрыш, противника, за первые n-шагов будет отображен в ячейках: AM14; AO14; AQ14; AS14;AU14. В столбце Шаг 3. Из Рис. 3 следует: так как максимальное значение равное 60 соответствует 3-й стратегии игрока 2, значит, новая стратегия игрока 1 – 3-я стратегия и накопленный выигрыш первого игрока составит: 0+40=40 при его 1-й стратегии; 20+30=50 при его 2-й стратегии; 60+0=60 при его 3-й стратегии. Из всех суммарных выигрышей наименьшим является 40, который получается при 3-й стратегии, следовательно, второй игрок должен взять именно эту стратегию для получения суммарного выигрыша в этой партии. 0+40=40 при его 1-й стратегии; 20+30=50 при его 2-й стратегии; 60+0=60 при его 3-й стратегии. Из всех суммарных выигрышей второго игрока наибольшим является 60, который получается при 3-й стратегии, следовательно, первым игроком должна быть взята именно эта стратегия. Расчет показателей первого игрока (А1), при n=2
Рис.4 Расчет показателей второго игрока (В1), при n=2
Рис.5 Все полученные данные занесены в таблицу ( Рис.4, Рис.5). В столбце Продолжая процесс далее, возможно получить ряд разыгрываний игры за 100 итераций (партий), и приближённое решение игры: x100=(0,6; 0,01; 0,39), y100=(0,21; 0,3; 0,49), n=24. Оптимальные стратегии для первого и второго игроков
Рис.6 Представленная программа рассчитана на 16 матричных комбинаций: ( i х j) , i = 2,..,5; j = 2,..,5. Вручную вводится матрица, ее размерность и MS Excel автоматически выдает ответ. Сходимость итераций, даже при небольшом расчете, дает возможность ориентировочного нахождения цены игры и доли частных стратегий, при увеличении же числа итераций решения значительно уточняются.
Поиск по сайту: |
 ik раз (i=1,…,m), а игрок 2 j-ю чистую стратегию
ik раз (i=1,…,m), а игрок 2 j-ю чистую стратегию 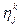 раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы
раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы  .
.
 - наибольшее значение проигрыша игрока 2 и
- наибольшее значение проигрыша игрока 2 и  - наименьшее значение выигрыша игрока 1.
- наименьшее значение выигрыша игрока 1.
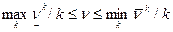 . (1)
. (1) .
. .
. .
.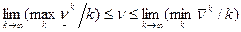 . (2)
. (2)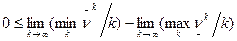 .
. .
. . Следовательно, в силу ограниченности пределов
. Следовательно, в силу ограниченности пределов  .
. для "e>0.
для "e>0. . Из неравенства (2) следует, что равенство пределов = n.
. Из неравенства (2) следует, что равенство пределов = n. .
. , и пошаговая демонстрация решения в MS Excel
, и пошаговая демонстрация решения в MS Excel


 находится наименьший средний выигрыш равный 0 игрока 1, полученный им в первой партии; в столбце
находится наименьший средний выигрыш равный 0 игрока 1, полученный им в первой партии; в столбце  стоит наибольший средний выигрыш равный 60, полученный игроком 2 в первой партии; в столбце n находится среднее арифметическое n=(
стоит наибольший средний выигрыш равный 60, полученный игроком 2 в первой партии; в столбце n находится среднее арифметическое n=( 

