|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЗВУКОВОЇ І ВІЗУАЛЬНОЇ ІНФОРМАЦІЇ ЦИВІЛЬНОГО ЛІТАКА
Горбунов А.В. ( ІАН НАУ, Україна)
Системи передачі даних (СПД) на даний час набули широкого розвитку і застосовуються у різних галузях науки, ЦА і виробництва (зв'язок, радіоелектроніка, енергетика, термоядерний синтез, медицина, космос, машинобудування, літальні апарати, обчислювальні комплекси і т.п.). Сучасні СПД представляють собою великі розгалужені мережеві системи, в яких носіями інформації є невеликі інформаційні блоки - ip-пакети. Ефективність роботи зазначених систем залежить від алгоритму за яким ip-пакети передаються в СПД, достовірності отриманої інформації та її якості тобто вибір оптимальної математичної моделі роботи системи зараз є досить актуальною проблемою Вступ. Характер і зміст задач дослідження в системах передачі даних (СПД) на борту цивільного літака визначається в кожному конкретному випадку конкретними умовами досліджень, а шлях їх розв’язку починається з ретельного вивчення об’єкту дослідження. Проведення класифікації та систематизації СПД на борту цивільного літака, яка підлягає дослідженню, дає змогу віднести її до систем деякого узагальненого типу, для яких вже є досить апробовані, а головне, існують ефективні методи їх моделювання та дослідження. Найбільш розповсюдженим типом таких систем є системи з використанням математичного апарату теорії масового обслуговування (СМО), фрактальні структури і ряди Фибоначчі з кроком золотого перетину, яки можна зустріти у різних технічних системах на борту цивільного літака та в інших сферах діяльності людини. В багатьох областях людської діяльності ми зустрічаємося з процесамироботи зазначених систем, яки залежать від алгоритму за яким ip-пакети передаються в СПД на борту цивільного літака, тому вони мають характер масового їх використання, особливо це відслідкується в цивільній авіації (ЦА). Найбільш простими і достатньо наочними прикладами таких процесів передачі даних є сліпи польоти, польоти у складних зовнішніх умовах, процеси посадки та зльоту літаків у великих аеропортах. Актуальність роботи полягає у наступному. Незважаючи на істотні відмінності у фізичному змісті різних прикладів використання СПД на борту цивільного літака , у них можна побачити багато спільного для різних типів літаків. Вважаємо, що у прикладах СМО для цивільних літаків поняття „обслуговування” необхідно сприймати і у прямому, і у переносному значенні цього слова. Таке сприйняття повинне виникати у зв’язку з тим, що усі операції, спрямовані на забезпечення безпеки польотів, тому можна їх розглядати як „обслуговування” цього кінцевого результату у ході реалізації технологічного процесу. Об’єкт, який надає будь-які „послуги” з обслуговування „клієнтів” , або літаків різного типу у масовому обсязі, можна назвати системою масового обслуговування. Під СМО на борту цивільного літака розуміють математичну динамічну систему, призначену для ефективного обслуговування деяких заявок (вимог), які потребують цього обслуговування в межах процесів експлуатації литака, або ремонту авіоніки. На практиці зустрічаються випадки, коли окремі споріднені СМО утворюють об’єднання, діяльність яких спрямована на досягнення тієї ж мети, що і кожної окремої СМО, але у більш широких масштабах, або у поглибленому виді. Сукупність таких взаємозалежних СМО називається мережею масового обслуговування на борту цивільного літака . Обмін інформацією в системах передачі даних також пропонується визначити як рух інформаційних пакетів від джерела до приймача в зазначених системах [1]. Основною математичною моделлю процесів, що описують трафік у телекомунікаційних мережах на борту цивільного літака , де проводились дослідження, є випадковий потік даних. Теорія масового обслуговування (ТМО), головною метою якої є розроблення математичних методів для пошуку основних характеристик масового обслуговування літаків, або авіоніки, оцінки якості функціонування обслуговуючої системи, у більшості випадків розглядає найпростіші потоки, коли імовірність надходження на обслуговування рівно “k” вимог в проміжок часу t задається формулою:
де l − щільність потоку вимог в одиницю часу. Формула (1) виражає закон розподілу Пуассона. Тому часто найпростіший потік називають пуассонівським. З (1) очевидно, що функція щільності f(z) випадкової величини xј при j>0 для найпростішого потоку має вигляд показового розподілу з параметром l.
де l − інтенсивність (щільність) потоку, яка для стаціонарних потоків з обмеженою післядією визначається виразом
де µ − середня довжина інтервалу між послідовними заявками. Як приклад стаціонарного потоку можна навести потік із рівномірним розподілом інтервалів часу між заявками. Функція щільності в цьому разі має вигляд:
Оскільки математичне очікування величини дорівнює b/2, то щільність потоку, що задається функцією (4.), дорівнює
Крім пуассонівських потоків розподілу в практиці дослідження систем масового обслуговування мають важливе значення потоки Ерланга. Потоком Ерланга порядку
де l*= lm. Легко показати, що інтервали xј при j > 1 потоку Ерланга порядку m представляються у вигляді суми m незалежних величин, що мають показовий розподіл із параметром l*. Вважаємо, що найпростіший потік задовольняє таким трьом основним вимогам. 1. Стаціонарність потоку, що означає, що для будь-якої групи з кінцевого числа відрізків часу , що не перетинаються, імовірність появи в них відповідно К1, ..., Кn вимог залежить тільки від цих чисел і довжин відрізків часу, але не залежить від їхнього розташування на осі часу, тобто імовірність появи К вимог в інтервалі часу (Т, Т+t) не залежить від Т і є функцією К і t. 2. Відсутність наслідку, яка полягає в тому, що імовірність надходження К вимог протягом (Т, Т+t) не залежить від того, скільки вимог і як вони надійшли до цього часу, тобто відсутність наслідку означає взаємну незалежність появи того або іншого числа вимог на пересічних відрізках часу. 3. Ординарність потоку вимог, що виражає практичну неможливість появи двох або декількох вимог у той самий момент часу,
де n − довжина інтервалу часу;
Слід зазначити, що найпростіші потоки в теорії масового обслуговування, яка використовується на борту цивільного літака і у практиці дослідження процесів функціонування складних систем наземного обладнання аеропортів грають дуже важливу роль і використовуються як математичні схеми для наближеного представлення реальних потоків звукової і візуальної інформації, що зустрічаються в практичних задачах дослідження систем. На практиці іноді зустрічаються і нестаціонарні потоки [2], що являють собою пуассонівський потік із змінними параметрами. Проте сутність використання того або іншого потоку не має якогось істотного впливу на процес створення математичних моделей систем масового обслуговування які використовуваються на борту цивільного літака . Алгоритм дослідження полягає у наступному. Після ознайомлення із методами математичного опису потоків однорідних подій, можна перейти до формального представлення процесів функціонування самих систем масового обслуговування які використовуваються на борту цивільного літака. Дамо стислу характеристику систем масового обслуговування які використовуваються на борту цивільного літака. У загальному випадку гіпотетична система масового обслуговування які використовуваються на борту цивільного літака може складатися з n - каналів, спроможних одночасно і незалежно друг від друга обслуговувати заявки (кожний інформаційний канал спроможний незалежно “обслуговувати” авіоніку літака. У будь-який момент часу канал знаходиться в одному із двох станів − вільний або зайнятий. Припустимо, що в деякий момент часу в систему (комплекс) надходить заявка. Якщо в цей момент є вільні канали, то заявка (або літак для диспетчера повітряного руху) приймається до обслуговування. У протилежному випадку заявка залишається в системі протягом деякого часу tn (час, скажімо, перебування літака в зоні обслуговування) як претендент на чергове обслуговування. За час tn заявка повинна бути прийнята до обслуговування, у протилежному випадку вона вважається загубленою (одержує відмову), а в нашому випадку не обслуговувается. Залежно від величини 1. Якщо tn = 0, то заявка, що надійшла, у даний момент часу або негайно приймається до обслуговування, якщо є вільні канали, або отримує відмову, якщо всі канали зайняті. Такі системи масового обслуговування які використовуваються на борту цивільного літака називаються системами з відмовою. Для цих систем показниками якості звичайно є імовірність відмови, середнє число відмов за даний інтервал часу тощо Середня частка відмов R(t0, t)визначається як
де
Для систем обслуговування з постійними параметрами і моментів часу достатньо віддалених від початку обслуговування, величина m(t0, t)також не залежить від t0 і може бути виражена співвідношенням
де lвідм − інтенсивність потоку відмов. Тоді середня частка відмов R дорівнює постійній величині
яка не залежить від тривалості інтервалу часу t. Величина (11) має сенс імовірності відмови для заявки, що надійшла в систему в довільний момент часу. 2. Якщо 3. Якщо 0< tn< ¥, заявка, що застала всі лінії зайнятими в момент надходження, очікує протягом tn у черзі, а після закінчення цього часу одержує відмову. Такі системи називаються змішаними. Ці системи одержали найбільше поширення, тому використовуваються на борту цивільного літака . Якість обслуговування в цьому випадку оцінюється імовірнісними характеристиками як кількості відмов, так і часу чекання, а в більшості випадків більш складними показниками − математичним очікуванням числа об’єктів які обслуговуються, що враховує обидва ці моменти якості обслуговування, або відверненого збитку, що враховує стратегічний виграш у конкретному обладнанні, яке використовуваються на борту цивільного літака Дуже важливо пам'ятати, що крім параметру tn для характеристики властивостей обслуговування необхідно задати також t3 − час обслуговування однієї заявки (час обслуговування літака з моменту його виявлення і як його називають інакше, час зайнятості каналу. Заявка, прийнята до обслуговування, займає один із каналів на час t3. Після закінчення цього часу канал звільняється і може приступити до обслуговування нової заявки. Як правило, tn і t3 вважаються випадковими величинами з заданими законами (або спільними законами) розподілу. Іноді припускають, що одна з них або обидві фіксовані. Дуже важливо знати при дослідженні систем які використовуваються на борту цивільного літака, як систем масового обслуговування, можливі найбільш поширені варіанти порядку зайняття каналів заявками, що надходять на обслуговування. Найбільш часто на практиці використовуються такі правила. 1. При відсутності черги заявок: - канали займаються в порядку їхніх номерів. Канал із колишнім номером не може бути притягнутий до обслуговування, якщо заявка не обслугована каналом із меншим номером; - канали займаються в порядку черги. Канал, що звільнився, надходить у чергу і не починає обслуговування заявок до використання всіх каналів, що звільнилися раніше (система контролю технічного стану авіоніки тощо); - канали займаються у випадковому порядку відповідно до заданих ймовірностей (наприклад, імовірність появи літака в зоні аеропорту). Якщо в момент надходження чергової заявки є nсв − вільних каналів, то в найпростішому випадку імовірність зайняти деякий вільний канал може бути прийнята рівною
У більш складних випадках імовірності Р1, ... ., Рn зайняти канал вважаються залежними від номерів каналів, моментів їхнього звільнення й інших параметрів (комплекси, групи комплексів, системи візуалізації польотної, або звукової інформації у цілому як системи масового обслуговування). 2. При наявності черги заявок (найбільш поширений випадок): - заявки приймаються до обслуговування в порядку черги. Канал, що звільнився, приступає до обслуговування тієї заявки, яка у найкоротший час може одержати відмову (літак знаходиться ближче інших); - заявки приймаються до обслуговування по мінімальному часі одержання відмови. Канал, що звільнився, приступає до обслуговування тієї заявки, яка у найкоротший час може одержати відмову (скажемо, літак, що може найближчим часом вийти з зони аеропорту); - заявки приймаються до обслуговування у випадковому порядку відповідно до заданих ймовірностей. Якщо в момент звільнення каналу у черзі є m заявок, то в найпростішому випадку імовірність вибрати для обслуговування деяку визначену заявку може дорівнювати q = 1m. У більш складних випадках імовірності q1, ... qm вважаються залежними від часу перебування заявки в системі, часу, що залишається до одержання відмови й інших параметрів. Встановлено, що дуже важливим і поширеним типом обслуговування авіоніки літака яка використовується на борту цивільного літака є обслуговування з перевагою (пріоритетом). Кожній заявці, що надходить у систему, приписується коефіцієнт переваги − пріоритет (наприклад, найбільш високий пріоритет постачальникам перешкод тощо). При цьому можуть бути різноманітні варіанти дисципліни черги. При одному із варіантів у момент звільнення каналу на обслуговування надходить заявка з черги, у якої пріоритет найбільший. При іншому варіанті можливо припинення обслуговування заявки, що займає канал, якщо в систему надійшла заявка з більшим пріоритетом, ніж у тієї, що була на обслуговуванні. Слід зазначити, що ми надалі будемо розглядати моделі систем масового обслуговування які використовуваються на борту цивільного літака для випадку, коли заявки утворюють найпростіший (пуассонівський) потік. Немає сумніву в тому, що для практики побудови складних систем масового обслуговування які використовуваються на борту цивільного літака становлять інтерес потоки заявок, які помітно відрізняються від найпростішого. Проте, з огляду на важливість методологічних аспектів, ми розглянемо найпростіші типи моделей і методику їхньої побудови. З історії питання.На початку XXI століття почалися радикальні зміни тих концептуальних положень, які визначають основні напрямки подальшого розвитку телекомунікаційної системи. Сформувалася ідея побудови мережі зв'язку наступного покоління, відома по абревіатурі NGN (Next Generation Network). Більшість фахівців уважає ідею NGN самою розумною концепцією подальшого розвитку инфокоммуникационной системи - симбіозу електрозв'язку й інформатики. У 2006 році в Санкт-Петербургскому НДІ була запропонована й обґрунтована математична модель тракту обміну ip-пакетамив NGN. Розроблено методику використання суб'єктивної оцінки якості зв'язку, сприйманої абонентом (R-фактора), як математично розрахункового критерію прийняття виклику на обслуговування. Проведено вимір і дослідження голосового трафіку на борту літака на пакетному ядрі GSM мережі, що використовує кодеки зі змінною інтенсивністю передачі інформації. Наскільки відомо [3], подібне дослідження трафіку в комерційної GSM мережі було проведено вперше в РФ. Сформульовано рекомендації із черговості зміни параметрів кодування бортової інформації викликів якщо буде потреба і зроблено скорочення займаної ними пропускної здатності на підставі проведеного дослідження впливу параметрів кодування голосових з'єднань на займану пропускну здатність й якість передачі мови на борту літака. Розроблено новий адаптивний алгоритм контролю доступу викликів у мережах зв'язку наступного покоління. Розроблено програмну реалізацію цього алгоритму мовою Java. Невизначеність попиту на нові види послуг визначена тими процесами, які почали міняти вигляд інфокомунікаційної системи на початку XXI століття. Ці зміни зазначені в останньому рядку таблиці 1. Вони входять до складу циклів, властиві історії розвитку телефонії. Таблиця 1 Циклічність у розвитку системи телефонного зв'язку
Розроблена імітаційна модель сегмента мережі зв'язку на борту літака наступного покоління. За допомогою цієї моделі проведене дослідження роботи запропонованого алгоритму у фіксованій і мобільній мережах зв'язку яка використовується на борту цивільного літака ; оцінене поліпшення кількісних й якісних показників роботи мережі при його впровадженні. Пропонується використання отриманих наукових і практичних результатів, але в новому аспекті з впровадженням сучасної теорії побудови фрактальної структури ip-пакетіві з кроком золотого перетину їх зміни в межах ряду Фибоначчі. Аналіз останніх досліджень в яких започатковано розв’язання даної проблеми, відділен-ня невирішених раніше частин загальної проблеми, як встановлене [4], показує, що вони не повною мірою забезпечують виконання очікуваних від них функцій. З технічних першоджерел [5] відомо, що потік як випадковий процес характеризується своїми статистичними власти-востями. Найчастіше використаються: щільність імовірності надходження даних за період, щільність імовірності інтервалів між надходженнями даних й в дослідженнях різних авторів по-перше всього розглядається автокореляційна функція даного процесу. Теоретично концепція NGN може бути реалізована в процесі розвитку будь-якої експлуатованої нині мережі електрозв'язку: телефонної, обміну даними яки використовуються на борту цивільного літака, кабельного телебачення. Гіпотетично можна розглядати ідею створення ще однієї - нової мережі, що повністю відповідає концепції NGN. Однак із практичної точки зору інтерес представляє тільки той спосіб побудови NGN, що заснований на цілеспрямованому розвитку телефонної мережі загального користування (ТФОП) для ЦА. При побудові NGN варто враховувати ряд специфічних властивостей системи телефонного зв'язку. Серед змін у ТФОП необхідно виділити перехід до пакетних технологій передачі й комутації, що стимулює розробку нових принципів побудови мережі. Одне з найважливіших завдань, що сприяє формуванню й реалізації цих принципів, - розробка методів розрахунку характеристик, які дозволяють аналізувати якість обслуговування трафика в NGN у цілому, а також у її окремих фрагментах. Дослідження принципів побудови телефонних мереж яки використовуються на борту цивільного літака пропонується розділити на два напрямки. Перший напрямок пов'язане з оптимізацією структури мережі в ЦА. Одне з основних завдань дослідження в даний роботи було сформульовано як пошук оптимального місця розміщення комутаційної станції. Другий напрямок стало актуальним при істотних якісних змінах в устаткуванні передачі й комутації, застосовуваному для розвитку ТФОП. Зокрема, з появою цифрових комутаційних станцій потрібна була розробка ряду нових принципів побудови телефонних мереж для ЦА. Постановка проблемиу загальному вигляді та її зв’язок із важливими науковими завданнями полягає в тому, щоб не тільки розібратися з явищем [6], але і запропонувати більш точні розрахунки окремих параметрів процесу для практичного використання на борту цивільного літака. Пошуки рішення проблем полягають в досліджені процесу руху ip-пакетів в інформаційних системах передачі даних яки використовуються на борту цивільного літака, але в складі CALS–технологій з математичними та практичними ототожненнями для отримання практичних результатів з метою вирішення проблемних питань в ЦА. Вирішення фундаментальної наукової проблеми - розробці нових принципів модернізації ТФОП, які спрямовані на формування мережі зв'язку на борту цивільного літака наступного покоління в NGN відповідно до вимог основних учасників інфокомуникаційного ринку: користувачів, операторів, виробників устаткування й постачаль-ників послуг. Для рішення поставлених у роботі завдань використалися методи теорії теле-трафика, оптимізації, керування розподілом ресурсів за допомогою Транспортної задачі (Тр._зад), системи підтримки та прийняття рішень (СППР) і експертних оцінок. Метою дослідженняє отримання кінцевого результату дослідження для визначення типу математичного розподілу трафіку в системах передачі даних на борту цивільного літака. Характеристики якості обслуговування трафика традиційно вважаються одним з найважливіших наукових напрямків у дослідженнях мереж телефонного зв'язку й обміну даними яки використовуються на борту цивільного літака. Отримані результати будуть корисні для дослідження характеристик якості обслуговування трафика в NGN. З іншого боку, принципи функціонування всіх пристроїв комутації в NGN мають специфіку, що обумовлена обраною технологією розподілу інформації. Із цієї причини необхідна розробка нових методів розрахунку ряду ймовірносно-тимчасових характеристик NGN, що адекватно відбиває процеси обміну інформацією між терміналами користувачів. Крім того, варто враховувати вплив якості обслуговування трафика в NGN на характеристики передачі інформації на борту цивільного літака. Зокрема, затримки пакетів приводять до зниження якості телефонного зв'язку. На етапі переходу до NGN міркування, викладені вище, визначають актуальність завдань вибору принципів модернізації ТФОП. До цих завдань ставляться також аналіз і розрахунок характеристик якості обслуговування трафика в NGN. Виклад основного матеріалу дослідженняз повним обґрунтуванням отриманих науко- вих результатів викладене в [5] почнемо з розгляду з пуассоновського потоку даних. Кла-сичною моделлю трафіку в інформаційних мережах на борту цивільного літака є Пуасоновський (найпростіший) потік. Він характеризується набором імовірностей P(k) надходження k повідомлень за часовий інтервал t
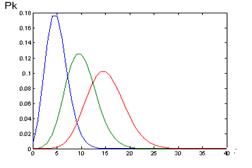
де k=0,1,... - число повідомлень; λ - інтенсивність потоку. Помітимо, що інтервал часу виміру кількості повідомлень t й інтенсивність потоку λ є постійними величинами. Сімейство Пуасоновських розподілів P(k) залежно від λ зображено на (рис.1). Більше значення λ відповідає більше широкому й симетричному графікові щільності ймовірності на (рис.2).
Рис.1. Пуасоновський розподіл. Рис.2. Графік випадкової функції, що приймає Щільності ймовірностей. дискретні цілі, тому має ненегативні значення. Математичне очікування (середнє) і дисперсія Пуасоновського потоку дорівнюють λt. Знаючи ймовірність надходження даних за період, можна одержати розподіл інтервалу τ між сусідніми подіями:
Звідси виcновок: пуасоновський потік характеризується експонентним розподілом інтервалів між подіями. Основною властивістю пуасоновського потоку, що обумовлює його широке застосування при моделюванні, є адитивність: результуючий потік суми пуасоновских потоків теж є пуасоновским із сумарною інтенсивністю:
При моделюванні пуасоновский потік можна одержати мультиплексуванням сукупності ON/OFF джерел, які називаються Марковскими процесами (рис.3.).
а) б) Рис.3 (а,б). Пуассоновський розподіл інформаційних ресурсів ip-пакетамив NGN. Вважається, що випадкова величина має розподіл з важким (вагомим) хвостом (РТХ або Heavy Tailed), якщо
Тобто хвіст розподілу загасає за статичним законом, на відміну від, наприклад, Гаусовського розподілу з експонентним убуванням хвоста. Результати експериментів у вигляді важкохвістного розподілу наведене на (рис.4).
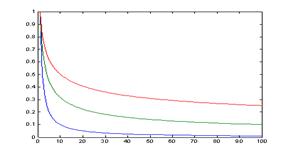
Рис. 4. Результати експериментів у Рис.5. АКФ ШУЗ (сині кольори) і АКФ ПУЗ вигляді важкохвістного розподілу. (зелений, червоний). Вважається, що мережний трафік у багатьох випадках найкраще описується саме важкохвістним розподілом, наприклад розподілом Парето [1]. Відомо [7], що автокореляція - кореляційний зв'язок між значеннями того самого випадкового процесу в рознесені моменти часу. Автокореляційна функція (АКФ) характеризує цей зв'язок. У загальному випадку АКФ характеризує внутрішню залежність між тимчасовим рядом і тим же поруч, але зрушеним на деякий проміжок (зрушення) часу, що називається лагом. Обчислення АКФ в експерименті здійснювалось по класичній формулі
де X з рисою - вибіркове середнє, k=0,1,2, ... Вважається [6], що процес має повільно убутну залежність (ПУЗ, long range dependence), якщо він характеризується АКФ, що убуває гіперболічно (за статичним законом) при збільшенні лага [1]. На противагу ПУЗ існує поняття швидко убутної залежності (ШУЗ). З поняттям ПУЗ зв'язана найважливіша прогнозуюча властивість - тривала пам'ять, що характеризується залежністю поточних параметрів процесу від попередніх. Численні сучасні дослідження трафіку свідчать про те, що він має властивість самоподоби [1]. Найпростішим самоподібними об'єктами є фрактали. Відповідно до визначення Мандельброта: "фрактал - структура, що складається із частин, які в якомусь змісті подібні до цілого" (Рис.5.). Тому самоподібні процеси часто називають фрактальними.
Рис.5. Схематичне формування фрактальної структури в межах ряду Фибоначчі. Неформально самоподібний процес визначається як випадковий процес, статистичні характеристики якого проявляють властивості масштабування. Строго самоподібний у широкому змісті процес (ССШП) характеризується інваріантістю АКФ при зміні рівня агрегування за умови МУЗ. На відміну від пуасоновських процесів самоподібні характеризуються наявністю післядії: імовірність надходження наступного (чергового) події залежить не тільки від часу, але й від попередніх подій (передісторії). Це означає, що число поточних подій може залежати від числа попередніх подій у віддалені проміжки часу. Тому одним з основних властивостей самоподібного процесу (self similar) є МУЗ (long range dependency). Найважливішим параметром, що характеризує ступінь самоподоби, є параметр Херста (Hurst) H, обумовлений для тимчасового ряду Xk,k=1,2,K N зі співвідношення
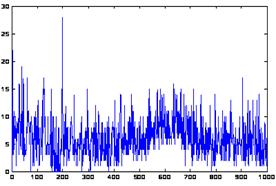
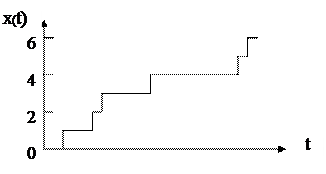
де R=max(Xk) - min(Xk) - розмах відхилення; α- стандартне відхилення, N - число членів тимчасового ряду, а - константа. Використовуючи значення показника Херста H, виділяють три типи випадкових процесів: 1. 0<=H<=0,5 - випадковим процес є антиперсистентним, або ергодичним, поруч, що не має самоподобу; 2. H = 0,5 - повністю випадковий ряд, аналогічний випадковим зсувам частки при класичному броунівскому русі; 3. H > 0,5 - персистентний (самопідтримуючий) процес, що має тривалу пам'ять й є самоподібним. Додатково слід зазначити, що самоподібний процес часто носить підривний (burst) характер, що виражається в можливості наявності викидів під час відносно низкою швидкості надходження подій. Стосовно до трафіку самоподоба виражається в незмінності поводження при зміні тимчасових масштабів спостереження й збереження схильності до сплесків при усередненні по шкалі часу. Аналіз отриманих експериментальних даних. З метою вивчення основних статистичних властивостей реального трафіку був проведений аналіз експериментальних даних. Об'єктом вивчення була магістраль 100 Мбит/с Інтернет провайдера на борту цивільного літака . Основною методикою одержання вихідних даних було перехоплення минаючих IP пакетів (за допомогою утиліти tcpdump) з подальшим перекладом в еквідистантну форму. 1) Відповідний часовий ряд залежності числа пакетів в одиницю часу (1 мс) на борту цивільного літака наведений на рис.6.
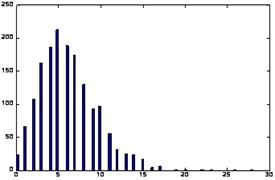
Рис. 6. Число пакетів в одиницю часу (1 мс). Рис. 7. Гістограма розподілу пакетів в одиницю часу (число пакетів/мс). 2) Гістограма для даного тимчасового ряду, що відбиває щільність розподілу числа пакетів в одиницю часу на борту цивільного літака , наведена на рис. 7. Візуально гістограма відповідає розподілу Пуасона, однак тест Колмогорова-Смирнова [2] спростовує цю гіпотезу, тобто потік даних все-таки не є найпростішим на борту цивільного літака. 3) АКФ даного тимчасового ряду наочно демонструє МУЗ (LRD), що характерно для фрактальних процесів.
4) Вимір параметра Херста підтверджують гіпотезу про самоподобу - H=0.8.
Рис. 8. АКФ тимчасового ряду числа пакетів в одиницю часу на борту цивільного літака . Висновкиі перспективи подальших досліджень в даному науковому напрямку полягають в тому, що вперше запропоновано нетрадиційній підхід до вирішення проблем на основі використання сучасної науки і математичного апарату. Встановлене фізичний зміст обміну ip-пакетамив NGN на борту цивільного літака, на якому базується розроблений метод. Визначене, що розподіл Інтернет трафіку на магістральному вузлі провайдера Інтернета близько до Пуасоновського, але їм не є. Потік даних є самоподібним. Близькість розподілу до Пуасоновського можна пояснити наявністю великого числа мультиплексування потоків, тому що об'єктом дослідження є магістральна лінія яка використовується на борту цивільного літака . Самоподоба можна розцінювати як фундаментальна статистична властивість мережного трафика, яких необхідно враховувати на практиці.
Література 1. Босікова І. І. Метод розв'язування систем лінійних алгебраїчних рівнянь з m-мірними матрицями // Кибернетика и системный анализ. — 2002. — № 1. — С. 37-47. 2. Кудрицький В. Д. Алгоритм нелінійної екстраполяції реалізацій скалярного випадкового процесу // Кибернетика и системный анализ. —2002. — № 1. — С. 47-53. 3. Хуанг Х., Пардалос П. M. Підхід до багатомірного розбиття для задач оптимізації // Кибернетика и системный анализ. — 2002. —№ 2. —С. 134-147. 4. Зайченко Ю. П., Заец И. 0., Камоцкий А. В., Павлюк Е. В. Исследование разных видов функций принадлежности параметров нечетких прогнозирующих моделей в нечетком методе группового учета аргументов / // УСиМ. — 2003. — № 2. — С. 56-67. 5. Sitnik А.G., Sitnianskikh L.M. Influential development principles and characteristics of the controllers on the information visualization systems in cockpit of the plane in order to increase the level of flight safety// The third world congress ” Aviation in the XX1 centuri“ “Safety in aviation and space technology”, September 22-24, 2008. 33.64- 33.69. 6. Михаль О.Ф., Руденко О.Г. Моделирование на сетях Петри виртуального вычислительного устройства для исследования эффективности локально-параллельных алгоритмов //УСиМ. — 2003. — № 3. —С. 18-28. 7. Молчанов И.Н., Чистякова Т.В. Интеллектуальное программное обеспечение для исследования и решения прикладных задач с приближенно заданными исходными данными // УСиМ. — 2003. — № 3. — С. 72-76.
Поиск по сайту: |
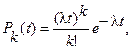
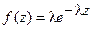 ,
,
 ,
,
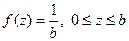 .
.
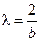 .
.
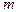 називається ординарний стаціонарний потік з обмеженим наслідком, для якого
називається ординарний стаціонарний потік з обмеженим наслідком, для якого ,
,

 − імовірність появи більш однієї вимоги.
− імовірність появи більш однієї вимоги. системи масового обслуговування які використовуваються на борту цивільного літака діляться на три істотно різних класи, які мають свою специфіку як у побудові процесу, так і в математичному формулюванні віднесених до них задач.
системи масового обслуговування які використовуваються на борту цивільного літака діляться на три істотно різних класи, які мають свою специфіку як у побудові процесу, так і в математичному формулюванні віднесених до них задач.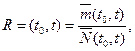
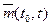 − середнє число відмов за інтервал часу (t0, t0+t);
− середнє число відмов за інтервал часу (t0, t0+t); − середнє число заявок, що надходять на обслуговування протягом інтервалу часу (t0, t0+t). У випадку стаціонарного вхідного потоку розмір
− середнє число заявок, що надходять на обслуговування протягом інтервалу часу (t0, t0+t). У випадку стаціонарного вхідного потоку розмір 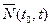 не залежить від t0 і дорівнює
не залежить від t0 і дорівнює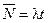
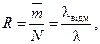
 = ¥, заявки, що надходять, відмов не одержують, а очікують (якщо всі канали зайняті) у черзі до того моменту, коли вони будуть прийняті до обслуговування. Ці системи називаються системами з чеканням. Показниками якості таких систем можуть бути середній час чекання заявки, середня довжина черги.
= ¥, заявки, що надходять, відмов не одержують, а очікують (якщо всі канали зайняті) у черзі до того моменту, коли вони будуть прийняті до обслуговування. Ці системи називаються системами з чеканням. Показниками якості таких систем можуть бути середній час чекання заявки, середня довжина черги. .
.
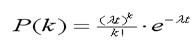 (13)
(13)




 λ
λ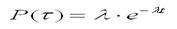 (14)
(14)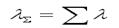 (15)
(15)
 (16)
(16)
 (17)
(17)
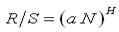 (18)
(18)