 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи по теме «Линейная алгебра»
Начальный уровень Второй семестр Задачи по теме «Функции двух переменных»
1. Найти частные производные первого порядка от функций:
2. Найти частные производные второго порядка от функций
3. Найти экстремумы функции двух переменных:
4. Найти частные производные от следующих функций и изобразить область определения:
1. Проинтегрировать дифференциальное уравнение, найти решение, удовлетворяющее данному условию, построить его график:
2. Проинтегрировать дифференциальное уравнение, построить интегральную кривую, проходящую через указанную точку
3. Найти решение задачи Коши для дифференциального уравнения с разделяющимися переменными:
4. Найти общее решение дифференциального уравнения с разделяющимися переменными:
5. Найти общее решение однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами:
6. Записать вид частного решения неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами по виду функции
7. Найти общее решение дифференциального уравнения:
Задачи по теме «Ряды»
1. Написать формулу п-го члена:
2. Исследовать сходимость ряда, используя следствие из необходимого условия сходимости:
3. Исследовать сходимость ряда с положительными членами с помощью признака Д/ Аламбера:
4. Исследовать сходимость ряда с положительными членами с помощью признака Коши:
5. При помощи сравнения с обобщённым гармоническим рядом или бесконечно убывающей геометрической прогрессией, исследовать сходимость ряда:
6. Исследовать знакопеременный ряд на абсолютную и условную сходимость:
7. Найти радиус и интервал сходимости степенного ряда:
8. Определить интервал сходимости степенного ряда и исследовать его сходимость на границах интервала:
Задачи по теме «Линейная алгебра»
1. Найти матрицу
2. Найти
3. Найти а) 4. Найти а) б) 5. Найти а) 6. Найти значение матричного многочлена а) б) в) г) д) e) 7. Вычислить определители:
8. Найти
9. Решить системы линейных алгебраических уравнений а) методом Крамера; б) методом обратной матрицы; в) методом Гаусса:
10. Найти решение системы а)
в) д) ж) и) 11. Даны точки: 12. Найти вектор 13. Заданы пары векторов: 1). 14. Даны два вектора 15. Даны точки 16. Даны векторы 17. Дано разложение вектора 18. Вычислить скалярное произведение
19. Найти косинус угла между векторами
20. Найти единичный вектор
21. Найти единичный вектор, направленный противоположно вектору 1) 22. На векторах 1) 23. Являются ли коллинеарными векторы
24. Являются ли ортогональными векторы
25. Даны точки 26. Даны векторы 27. Даны векторы: 28. Даны векторы: 29. 30. Даны точки 31. Даны векторы 32. Даны вершины четырехугольника A(1;-2;2), B(1;4;0), C(-4;1;1), D(-5;-5;3). Доказать, что диагонали взаимно перпендикулярны. 33. Даны точки А1(0;1;2), А2(1;2;4), B1(-1;-1;3), B2(1;0;0). Найти координаты вектора 34. Даны точки A(-1;2;3), B(-1;3;1), C(-1;7;3), D(-1;6;5). Доказать, что ABCD – прямоугольник. 35. Дан треугольник с вершинами 36. Проверить, будет ли треугольник с вершинами A(6;-4;2), B(3;2;3), C(3;-5;-1) прямоугольным? 37. Даны точки A(-3;-2;0), B(3;3;1), C(5;0;2). Во сколько раз 38. На векторах 39. При каком значении 40. Дан вектор 41. Даны векторы 42. Даны точки M(1;1;4), N(1;4;4), K(3;3;2). Доказать, что векторы 43. Найти угол между векторами 44. На векторах 45. Определить длины сторон параллелограмма, диагоналями которого служат векторы 46. Образует ли система векторов ортогональный базис? Если да, то постройте по этому ортонормированному, базису соответствующий ортогональный базис 47. Даны три вектора: 1) 48. Даны векторы
Поиск по сайту: |
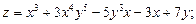



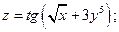
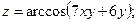

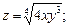

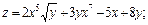

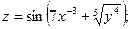






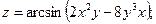

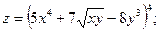







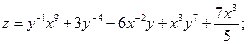




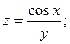

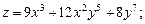

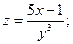
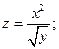


 ;
;

 3).
3). 
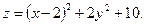 4).
4). 
 7).
7). 
 8).
8). 

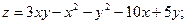






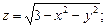

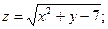












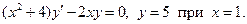










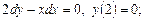 7).
7). 
 8).
8). 
 11).
11).  13).
13).  15).
15). 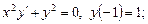 17).
17). 
 12).
12).  14).
14).  16).
16).  18).
18). 
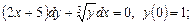 21)
21) 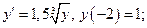 23).
23). 
 22).
22).  24).
24). 
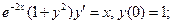









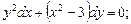







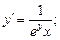













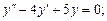

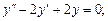

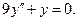

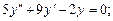






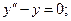



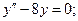

 :
:







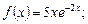


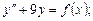








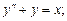





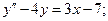
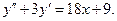







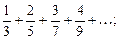



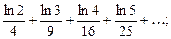














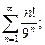








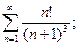







 ;
;



 .
.


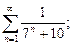
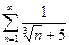
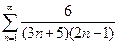





 16).
16). 
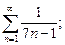 17).
17). 
 18).
18). 
 19).
19). 
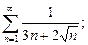 20).
20). 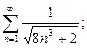

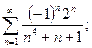
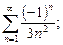


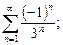


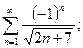
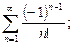


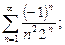




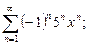





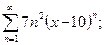


 ;
;
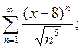
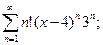








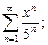



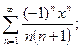

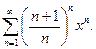
 , если
, если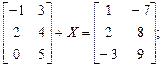


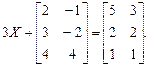
 и
и  , если эти произведения существуют:
, если эти произведения существуют:


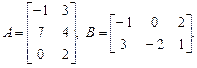


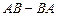
 б)
б) 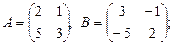
 и
и 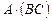
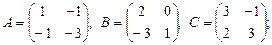
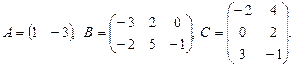
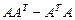
 б)
б) 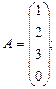 в)
в) 

 если
если ;
;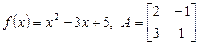
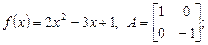
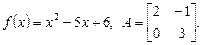
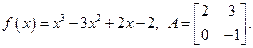
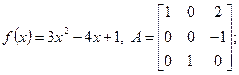
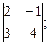

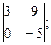

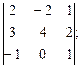
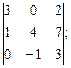



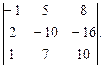


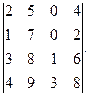





 и сделать проверку, если
и сделать проверку, если 

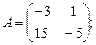



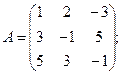
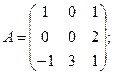
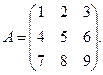




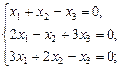

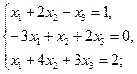


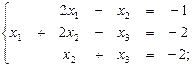 б)
б) 
 г)
г) 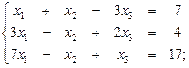
 е)
е) 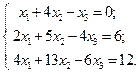
 з)
з) 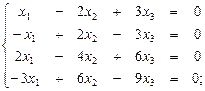
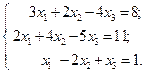 к)
к) 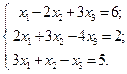
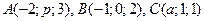 . При каких значениях
. При каких значениях  и
и  векторы
векторы  и
и  равны?
равны?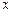 из уравнения
из уравнения  , если
, если  ,
,  ,
, 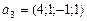 .
.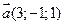 и
и  ; 2).
; 2).  и
и 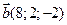 ; 3).
; 3).  и
и  ; 4).
; 4). 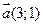 и
и  ; 5).
; 5).  и
и  ; 6).
; 6).  и
и  ; 7).
; 7).  и
и  . Среди этих пар укажите те, которые удовлетворяют следующим условиям: а)
. Среди этих пар укажите те, которые удовлетворяют следующим условиям: а)  и
и  коллинеарные; б) длина вектора
коллинеарные; б) длина вектора  , длина вектора
, длина вектора  ; в) скалярное произведение векторов
; в) скалярное произведение векторов 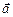 и
и 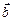 равен
равен  ; д) угол между векторами
; д) угол между векторами  ; е) векторы
; е) векторы  . Проверить, что векторы
. Проверить, что векторы  ,
,  ,
,  и
и  . Проверить, что векторы
. Проверить, что векторы 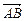 и
и  коллинеарные. Установить, во сколько раз один длиннее второго.
коллинеарные. Установить, во сколько раз один длиннее второго. и
и 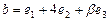 , где
, где  ,
,  ,
,  — базис. При каких значениях
— базис. При каких значениях  и
и  векторы
векторы  и
и  коллинеарные?
коллинеарные? по базису
по базису  . Разложить вектор
. Разложить вектор  по этому базису, если эти векторы коллинеарные и противоположно направлены, а
по этому базису, если эти векторы коллинеарные и противоположно направлены, а 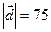 .
. :
:








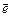 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 


 2)
2) 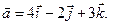
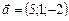 и
и  2)
2) 




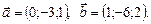




 . Определить длину вектора
. Определить длину вектора  .
. и
и  . Найти
. Найти  и
и  .
.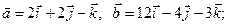 б)
б) 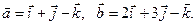 Определить длины векторов и косинус угла между ними.
Определить длины векторов и косинус угла между ними. При каком значении
При каком значении  косинус угла между ними будет равен 5/12?
косинус угла между ними будет равен 5/12? . Найти скалярное произведение
. Найти скалярное произведение  .
.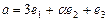 и
и  в базисе
в базисе 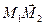 и
и  , если точки M1 и M2 –середины отрезков A1 B1 A2 B2 соответственно.
, если точки M1 и M2 –середины отрезков A1 B1 A2 B2 соответственно. . Найти векторы, совпадающие с его сторонами и вычислить его периметр.
. Найти векторы, совпадающие с его сторонами и вычислить его периметр. больше (меньше)
больше (меньше) 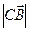 ?
? и
и  построен треугольник. Доказать, что треугольник прямоугольный и найти его площадь.
построен треугольник. Доказать, что треугольник прямоугольный и найти его площадь.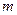 векторы
векторы 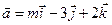 и
и  взаимно перпендикулярны?
взаимно перпендикулярны? . Найти координаты вектора
. Найти координаты вектора  , лежащего в плоскости Oxy , если
, лежащего в плоскости Oxy , если 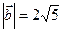 и векторы
и векторы  и
и 
 . При каких значениях
. При каких значениях 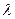 векторы
векторы  и
и  перпендикулярны, если точка O – середина отрезка MK.
перпендикулярны, если точка O – середина отрезка MK. и
и  , если A(3;3;-2), B(0;-3;4), C(0;-3;0), D(0;2;-4).
, если A(3;3;-2), B(0;-3;4), C(0;-3;0), D(0;2;-4). и
и  построен параллелограмм. Вычислить длины его диагоналей.
построен параллелограмм. Вычислить длины его диагоналей. и
и  .
. (1;1;0;-1;-1), (1;0;-1;0;1), (1;-1;2;-1;1), (1;-1;0;1;-1).
(1;1;0;-1;-1), (1;0;-1;0;1), (1;-1;2;-1;1), (1;-1;0;1;-1).
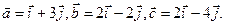
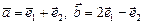 , где
, где 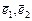 - базис,
- базис,  ,
,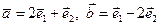 , где
, где