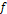|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ИССЛЕДОВАНИЕ ВЛИЯНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ЭЛЕМЕНТОВ МАЯТНИКА НА ПОКАЗАТЕЛИ ДИНАМИКИ КОЛЕБАТЕЛЬНОГО ПРОЦЕССА
Рассмотрены математические преобразования (с использованием уравнения Лагранжа) для получения уравнений фазовой траектории и первообразной для расчёта времени движения маятника. Получены графики фазовой траектории и кривая времени колебания маятника. Установлено, что колебания маятника (при определенных геометрических параметрах) могут не существовать в природе и их отображение на графике возможно только в мнимой плоскости. Проведен анализ влияния геометрических параметров на показатели динамики колебательного процесса.
Как правило, моделирование объектов, помимо чисто научных целей может иметь и прикладное значение. Для проектирования и анализа механических систем (например, математического маятника) нужно разработать специальный физико-математический аппарат. Любой механизм можно представить в виде совокупности звеньев и сопряжений. Например, маятник с зазором (рис. 1) представляет собой последовательное соединение звеньев [1].
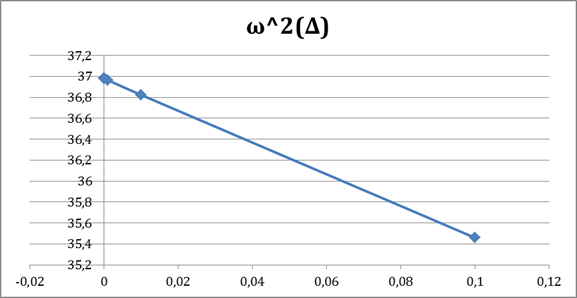
Рис. 1. Модель математического маятника с зазором и опорой Целью данной публикации является разработка математического аппарата, который позволит исследовать влияние геометрических параметров маятника (величины зазора и длины планки) на значение фазовой траектории и времени движения маятника. Математический маятник представляет собой идеальную модель, в которой материальная точка массой m подвешена на невесомой и нерастяжимой планке длиной l0. В такой системе происходят периодические колебания, которые можно рассматривать как вращение маятника вокруг оси. 1. Неподвижной оси, на которой закреплён маятник. 2. Зазор 3. Планка подвеса маятника l0. 4. Материальная точка m (подвес). Примем Запишем уравнение Лагранжа 2 рода [2]:
T – кинематическая энергия ( где J – момент инерции (
где П – потенциальная энергия ( Выразим уравнение Лагранжа с помощью введенных обозначений:
Вычислим производные:
Подставим Т,П и их производные в уравнение Лагранжа:
Понизим порядок уравнения:
Решим уравнение подстановкой
Уравнение с разделяющимися переменными:
Подставим v:
Интегрируем обе части:
Учитывая, что:
Получим:
Из начальных условий:
Найдём:
Тогда:
Физический смысл Найдём из соотношения (1):
Т.к.
Проинтегрируем обе части:
Из начальных условий, видно, что:
Исследуем соотношение (1) при:
l = 300 мм (0.3 м) g = 10 Рассчитаем значение фазовой траектории маятника для
Таблица 1 – Значения фазовой траектории маятника
Из расчитанных значений видно, что для (
Рис. 2. Фазовая траектория маятника в полярных координатах Для определения зависимости величины зазора на значение фазовой траектории маятника зафиксируем значение
Таблица 2 – Зависимость фазовой траектории от величины зазора
Построим график зависимости фазовой траектории от величины зазора (рис. 3).
Рис. 3. Зависимость фазовой траектории от величины зазора Из графика зависимости фазовой траектории от величины зазора видно, что при увеличении величины зазора прямо пропорционально увеличивается значение фазовой траектории маятника. Для определения зависимости величины длины планки маятника на значение фазовой траектории маятника зафиксируем значение
Таблица 3 – Зависимость фазовой траектории от длины планки маятника
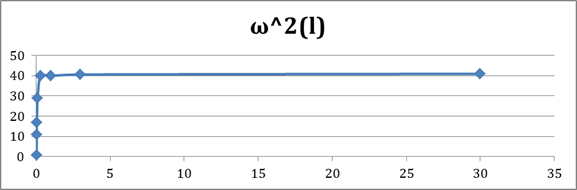
Построим график зависимости фазовой траектории от длины планки маятника (рис. 4). Рис. 4. Зависимость фазовой траектории от длины планки маятника
Из графика зависимости фазовой траектории от длины планки маятника видно, что при увеличении длины планки маятника до 1 м, происходит резкое увеличение значения фазовой траектории, а на интервале от 3 до 30 м, значение фазовой траектории практически неизменно. Исследуем соотношение (2) при:
l = 300 мм (0.3 м) g = 10 Рассчитаем значение времени движения маятника для
Таблица 4 – Значения времени движения маятника
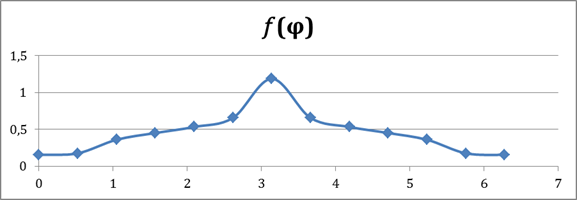
Из расчитанных значений видно, что значения времени колебания для диапазона
Рис. 5. Кривая времени движения маятника Для определения зависимости величины зазора на значение времени движения маятника зафиксируем значение
Таблица 5 – Зависимость времени движения маятника от величины зазора
Построим график зависимости времени движения маятника от величины зазора (рис. 6) Рис. 6. Зависимость времени движения маятника от величины зазора Из графика зависимости времени движения маятника от величины зазора видно, что при увеличении величины зазора происходит экспоненциальной увеличение времени движения маятника.
Для определения зависимости величины длины планки маятника на значение времени движения маятника зафиксируем значение
Таблица 6 – Зависимость времени движения маятника от длины планки
Построим график зависимости времени движения маятника от длины планки (рис. 7) Рис. 7. Зависимость времени движения маятника от длины планки Из графика зависимости времени движения маятника от длины планки видно, что при незначительном увеличении длины планки (до 1 м) происходит экспоненциальное уменьшение времени движения маятника. Увеличение длины планки маятника выше 1 м не влияет на изменение времени движения маятника.
ВЫВОДЫ
1. Разработана математическая модель маятника с зазором. 2. Получены формулы для расчёта фазовой траектории и времени движения маятника. 3. Анализ влияния геометрических параметров маятника на показатели динамики колебательного процесса показал: – при увеличении величины зазора прямо пропорционально увеличивается значение фазовой траектории маятника; – при увеличении длины планки маятника до 1 м, происходит резкое увеличение значения фазовой траектории, а на интервале от 3 м и выше, значение фазовой траектории практически неизменно; – при увеличении величины зазора происходит экспоненциальное увеличение времени движения маятника; – при увеличении длины планки до 1 м происходит экспоненциальное уменьшение времени движения маятника. Увеличение длины планки маятника выше 1 м не влияет на изменение времени движения маятника.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Поиск по сайту: |

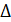 между осью и планкой на которой закреплен маятник.
между осью и планкой на которой закреплен маятник.
 – обобщённая сила
– обобщённая сила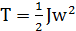 ),
), ), тогда:
), тогда: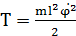 ,
, 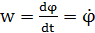
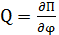 ,
,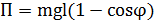 )
)
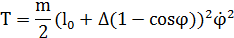
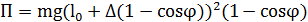
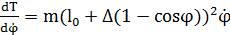 ;
;
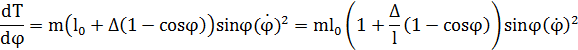
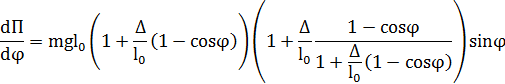
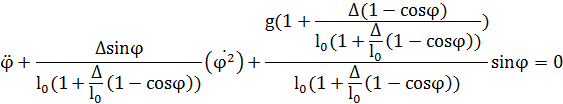
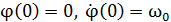 – начальные условия
– начальные условия
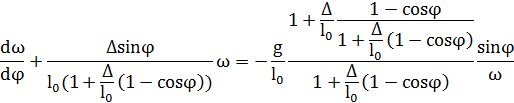
 [3]:
[3]: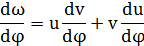


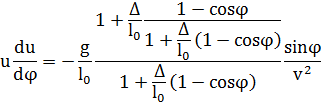
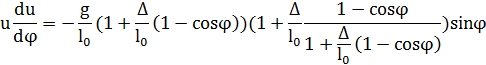
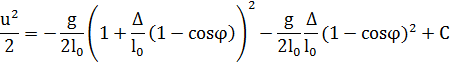

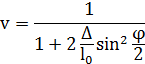
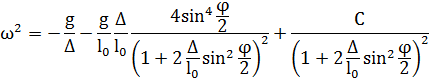

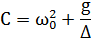
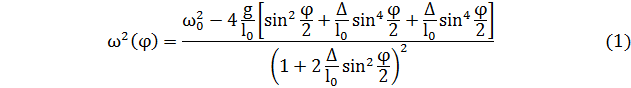
 – фазовая траектория маятника [4].
– фазовая траектория маятника [4].
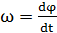 , то
, то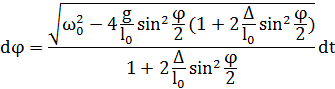

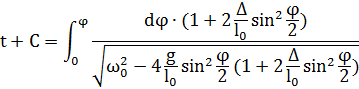
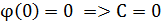

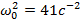
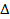 = 0.01 мм (0.0001 м)
= 0.01 мм (0.0001 м)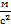
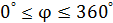 (табл. 1)
(табл. 1)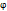

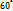

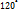
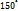
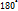
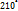

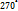
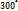
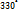
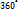
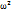

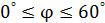 ) и, следовательно, для (
) и, следовательно, для ( 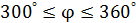 ) – имеем реальные колебания маятника (возможно отображение колебаний в реальной плоскости), остальные же диапазоны угла
) – имеем реальные колебания маятника (возможно отображение колебаний в реальной плоскости), остальные же диапазоны угла 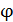 находятся в мнимой плоскости (в природе не существуют). Построим график фазовой траектории маятника в полярных координатах (рис.2)
находятся в мнимой плоскости (в природе не существуют). Построим график фазовой траектории маятника в полярных координатах (рис.2)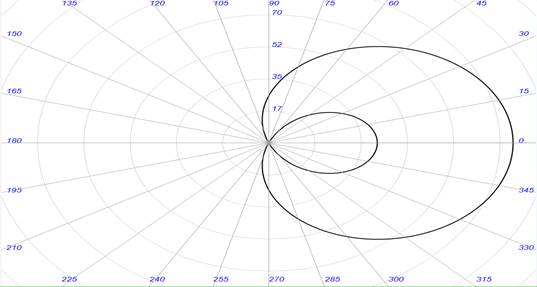
 иl = 0.3 м и составим таблицу расcчитанных значений (табл. 2).
иl = 0.3 м и составим таблицу расcчитанных значений (табл. 2).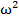
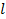
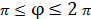 (табл. 4)
(табл. 4)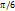
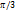


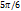
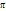
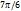
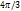

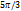
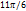

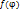
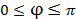 равны значения для
равны значения для 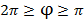 . Экстремум функции в точке
. Экстремум функции в точке  . Построим график времени движения маятника (рис.5)
. Построим график времени движения маятника (рис.5)