 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Момент импульса. Тензор инерции
Момент импульса тела относительно неподвижной точки - важнейшее понятие в динамике вращательного движения твердого тела. Он определяется так же, как и для системы материальных точек:
Здесь С учетом постоянства расстояний между точками абсолютно твердого тела вектор момента импульса L удается связать с вектором угловой скорости Рассмотрим, к примеру, две одинаковые точечные массы
Здесь учтено, что
Существенно, что в этом примере вектор L, направлен так же, как и
Получим выражение для L в случае твердого тела произвольной формы, закрепленного в некоторой точке О. Пусть
Векторы Итак, в системе xyz
Тогда, продолжая (2.3), можно записать:
Выражения для проекций момента импульса на оси системы xyz запишем в следующем виде:
или
где
Диагональные элементы тензора Если координатам x, y и z присвоить номера 1, 2 и 3 соответственно, то (2.9-2.11) можно представить в виде
В символическом виде можно записать так:
Самое главное, что стоит за приведенными выше формулами, заключается в следующем. Девять величин
Итак, мы столкнулись с новым типом величин, имеющим важное значение в физике - тензором. Если для задания скалярной величины необходимо одно число (значение скалярной величины), векторной - три числа (три проекции вектора на оси декартовой системы координат), то для задания тензора необходимы в общем случае 9 чисел. На языке математики тензор - это многокомпонентная величина, характеризующаяся определенным поведением при преобразованиях системы координат (в данном случае компоненты тензора инерции преобразуются как произведения соответствующих координат).
Поиск по сайту: |

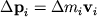 - импульс элементарной
- импульс элементарной  в лабораторной системе XYZ, а
в лабораторной системе XYZ, а  - радиус-вектор массы
- радиус-вектор массы 
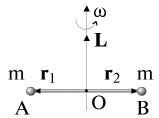
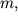 укрепленные на концах невесомого стержня АВ (рис. 2.В). Стержень с массами вращается с угловой скоростью
укрепленные на концах невесомого стержня АВ (рис. 2.В). Стержень с массами вращается с угловой скоростью 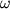 вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае
вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае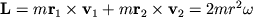
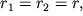 а
а 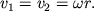
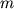 на концах жестко закреплен на вертикальной оси (в точке О) под некоторым углом
на концах жестко закреплен на вертикальной оси (в точке О) под некоторым углом  к ней и лежит в плоскости Oyz. При вращении стержня вокруг вертикальной оси с угловой скоростью
к ней и лежит в плоскости Oyz. При вращении стержня вокруг вертикальной оси с угловой скоростью 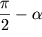 с осью z. Система xyz, введенная в начале лекции 1, жестко связана со стержнем и поворачивается вместе с ним. При этом вектор L остается в плоскости Oyz, а в лабораторной системе движется по конической поверхности с углом полураствора
с осью z. Система xyz, введенная в начале лекции 1, жестко связана со стержнем и поворачивается вместе с ним. При этом вектор L остается в плоскости Oyz, а в лабораторной системе движется по конической поверхности с углом полураствора 
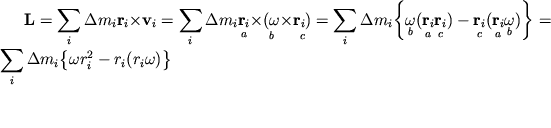
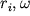 и L можно проектировать как на оси лабораторной системы XYZ, так и на оси системы xyz, жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы xyz заключается в том, что в ней проекции
и L можно проектировать как на оси лабораторной системы XYZ, так и на оси системы xyz, жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы xyz заключается в том, что в ней проекции 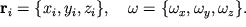

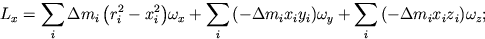
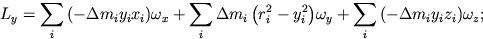
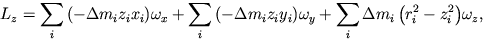
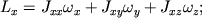


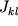 - 9 компонент так называемого тензора инерции
- 9 компонент так называемого тензора инерции 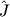 твердого тела относительно точки О:
твердого тела относительно точки О:
 называются осевыми моментами инерции, недиагональные элементы
называются осевыми моментами инерции, недиагональные элементы 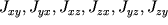 называются центробежными моментами инерции. Обратим внимание, что
называются центробежными моментами инерции. Обратим внимание, что 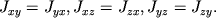 Такой тензор называют симметричным.
Такой тензор называют симметричным.
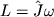
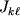 (из них шесть независимых) определяют однозначную связь между L и
(из них шесть независимых) определяют однозначную связь между L и  причем оказывается, что L, вообще говоря, не совпадает по направлению с
причем оказывается, что L, вообще говоря, не совпадает по направлению с 