 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Политропический процесс
В параграфе 2.4 отмечалось, что важным классом термодинамических процессов являются процессы, происходящие при постоянной теплоемкости, то есть политропические процессы. К таким процессам, в частности, относятся адиабатический, изотермический, изобарический и изохорический процессы. Для идеального газа нетрудно получить уравнение политропического процесса тем же способом, которым ранее было выведено уравнение Пуассона. Пусть молярная теплоёмкость идеального газа в политропическом процессе равна
из которого следует:
Подставляя это выражение в формулу (2.76) получим
или с учетом соотношения Майера (2.70)
Сравнение формул (2.100) и (2.102) при условии, что
аналогичное уравнению (2.79). Здесь введен параметр
который называется показателем политропы. Из этой формулы можно также получить зависимость молярной теплоемкости
Преобразование формулы (2.103) к виду:
и интегрирование полученного уравнения дает
Уравнение (2.107) называется уравнением политропического процесса или политропы – кривой, описываемой таким уравнением в переменных Аналогично уравнениям адиабаты (2.86) и (2.87) уравнение политропы может быть переписано в других термодинамических координатах:
При адиабатическом процессе Если процесс изотермический, то Для изобарического процесса при При изохорическом процессе Если умножить уравнение (2.100) на величину
При
Отсюда имеем Для политропических процессов значение теплоёмкости и, соответственно, показателя политропы могут принимать любые величины. Отрицательные значения теплоёмкости, когда показатель политропы В соответствии с формулой (2.100) при Рассуждая аналогичным образом, можно на основании формулы (2.102) установить связь между приращениями давления и температуры. При Работа газа в политропическом процессе может быть определена с помощью интеграла (1.13) при подстановке в него уравнения политропы(2.107), аналогично тому, как это сделано в формуле (2.97):
Интегрирование в выражении (2.112) дает формулу для определения работы в политропическом процессе
где: Из этой формулы, в частности, следует, что работа при расширении газа всегда остаётся положительной, независимо от того, какое значение принимает показатель политропы, больше или меньше единицы. Нетрудно видеть, что для адиабатического процесса при
где учтено, что при этом процессе Формула (2.113) неприменима для описания изохорического процесса, так как при выводе уравнения политропы (2.103) исключался случай Другим процессом, не описывающимся соотношением (2.113), является изотермический процесс. Как было сказано выше, он является предельным случаем политропического процесса при
или
где учтено постоянство температуры в этом процессе: Поскольку внутренняя энергия идеального газа не изменяется в изотермическом процессе, количество теплоты, полученное газом, также может быть рассчитано по этой формуле, то есть в этом процессе В заключение параграфа запишем все полученные формулы в единую таблицу 2.1.
Задача 2.4. Какова молярная теплоёмкость Решение: Так как по условию задачи
или
Тогда, с учетом одноатомности газа (число степеней свободы
а показатель политропы соответственно будет равен:
Задача 2.5. Какая работа совершается одним молем идеального газа в политропическом процессе с показателем политропы Решение: Используя уравнение политропы (2.108):
Отсюда имеем:
Следовательно, работа, совершаемая одном молем идеального газа в процессе с постоянной теплоёмкостью, определяется только разностью температур конечного и начального состояний газа. Таким образом, для идеального газа работа, а, следовательно, и количество теплоты, в политропических процессах определяются только конечным и начальным состояниями системы, так как путь перехода из одного состояния в другое определён теплоёмкостью газа (показателем политропы). Однако даже при рассмотрении только политропических процессов, работу и количество теплоты нельзя считать функцией состояния системы, так как переход из одного состояния в другое может быть осуществлен последовательностью различных политропических процессов. Задача 2.6. Какое количество теплоты передано одноатомному газу в процессе, описанному в условии задачи 2.5? Решение: В соответствии с формулой (2.105) имеем:
Тогда количество теплоты будет равно:
Отсюда, в частности, следует, что при равенстве показателя политропы показателю адиабаты для одноатомного газа:
Поиск по сайту: |
 . Тогда в соответствии с первым началом термодинамики (1.5) имеем выражение:
. Тогда в соответствии с первым началом термодинамики (1.5) имеем выражение: ,
,
 .
.

 .
.
 , позволяет записать уравнение
, позволяет записать уравнение ,
,
 ,
,
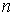 :
: .
.

 .
.
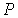 и
и  .
. ,
,
 .
.
 , что соответствует нулевой теплоемкости. Подставив
, что соответствует нулевой теплоемкости. Подставив  в формулу (2.104) и сравнив получившееся выражение с (2.80), имеем
в формулу (2.104) и сравнив получившееся выражение с (2.80), имеем  , и уравнение политропы (2.107) становится уравнением адиабаты:
, и уравнение политропы (2.107) становится уравнением адиабаты:  .
. , так как при этом
, так как при этом  . В этом случае показатель политропы
. В этом случае показатель политропы  . Обратим внимание на то, что поскольку при выводе уравнения политропы мы исключали величину
. Обратим внимание на то, что поскольку при выводе уравнения политропы мы исключали величину  , то этот вывод не может считаться полностью корректным для изотермического процесса.
, то этот вывод не может считаться полностью корректным для изотермического процесса.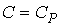 показатель политропы
показатель политропы  , и уравнение (2.107) принимает форму:
, и уравнение (2.107) принимает форму:  .
. , что соответствует случаю, когда показатель
, что соответствует случаю, когда показатель  . Очевидно, переход в формуле (2.107) к указанному пределу некорректен. Это связано с тем, что при выводе уравнения политропы предполагалось, что
. Очевидно, переход в формуле (2.107) к указанному пределу некорректен. Это связано с тем, что при выводе уравнения политропы предполагалось, что  (см. переход к формуле (2.103)).
(см. переход к формуле (2.103)). и сложить его с уравнением (2.102), предварительно умноженным на величину
и сложить его с уравнением (2.102), предварительно умноженным на величину  , то получим уравнение политропы в дифференциальном виде
, то получим уравнение политропы в дифференциальном виде .
.
 это уравнение приобретает форме:
это уравнение приобретает форме:
 или
или  . Из уравнения (2.110) также следует, что в процессе, при котором
. Из уравнения (2.110) также следует, что в процессе, при котором  .
. величины
величины  и
и  с ростом объёма газа его температура растёт. В соответствии с первым началом термодинамики этот рост должен быть обеспечен подводом к системе дополнительного количества теплоты.
с ростом объёма газа его температура растёт. В соответствии с первым началом термодинамики этот рост должен быть обеспечен подводом к системе дополнительного количества теплоты. с ростом давления температура газа будет возрастать, а при
с ростом давления температура газа будет возрастать, а при  - уменьшаться.
- уменьшаться. .
.
 ,
,
 и
и  - начальные давление и объём газа,
- начальные давление и объём газа,  - его конечный объём.
- его конечный объём. выражение (2.113) переходит в формулу (2.95). Для изобарического процесса, при
выражение (2.113) переходит в формулу (2.95). Для изобарического процесса, при  ,
,
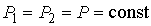 .
. , а затем выполнить интегрирование. Тогда имеем
, а затем выполнить интегрирование. Тогда имеем
 ,
,
 .
. . При изотермическом расширении идеального газа работа совершается только за счёт теплоты, подведённой из окружающей среды.
. При изотермическом расширении идеального газа работа совершается только за счёт теплоты, подведённой из окружающей среды.

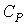





 , то в соответствии с первым началом термодинамики имеем:
, то в соответствии с первым началом термодинамики имеем:
 .
. ), молярную теплоемкость можно определить по формуле:
), молярную теплоемкость можно определить по формуле: ,
,
 ?
? и уравнение Клапейрона-Менделеева для одного моля
и уравнение Клапейрона-Менделеева для одного моля  , перепишем (2.113) в виде:
, перепишем (2.113) в виде: .
. .
. .
. .
. , количество теплоты
, количество теплоты  .
.