 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ТЕМА 2. Векторная алгебра
1. Линейные действия над векторами (сложение, вычитание, умножение на число). 2. Нелинейные действия с векторами (скалярное произведение, векторное произведение, смешанное произведение). 3. Решение задач с помощью векторной алгебры. Условие коллинеарности, условие перпендикулярности, условие компланарности векторов.
Решение типового варианта контрольной работы. Задание 1: Коллинеарны ли векторы Решение: 1. Вычислим проекции векторов
2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:
Задание 2: Перпендикулярны ли векторы Решение:Два вектора перпендикулярны , если их скалярное произведение равно 0,скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле:
Задание 3: Компланарны ли векторы Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле:
Задание 4: При каком значении Решение: 1) Для определения
Задание 5: Даны точки: Найти: 1. пр 2. 3. 4. орт вектора 5. 6. 7. Решение: 1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: пр
на основании формулы, выше написанной, получим :
2. Для нахождения длины вектора воспользуемся формулой:
Итак: 3. Угол между векторами можно найти из определения скалярного произведения:
4. Направление вектора Итак: орт вектора 5. Скалярное произведение векторов вычисляем по формуле:
Итак: 6. Векторное произведение векторов вычисляется по формуле:
Находим проекции векторов на оси координат:
Итак: 7. Смешанное произведение векторов вычисляется по формуле:
Задание 6:Даны координаты вершин пирамиды:
Вычислить: 1. объем пирамиды; 2. длину ребра 3. площадь грани Решение: 1. Объем пирамиды равен параллелипипеда, построенного на векторах как на ребрах равен:
Найдем проекции соответствующих векторов на оси координат:
Тогда объем пирамиды равен:
Вычислим объем по указанной формуле:
2. Длина ребра
3. Площадь грани
Контрольная работа
Поиск по сайту: |
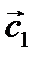 и
и  , разложенные по векторам
, разложенные по векторам  и
и  , где
, где 
 на оси координат:
на оси координат:

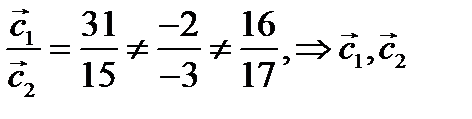 не коллинеарны.
не коллинеарны. ?
? , где
, где 
 вычислим скалярное произведение:
вычислим скалярное произведение: векторы не перпендикулярны.
векторы не перпендикулярны. ?
? , где
, где  вычислим смешанное произведение векторов:
вычислим смешанное произведение векторов: векторы не компланарны.
векторы не компланарны. векторы
векторы  где
где  , перпендикулярны?
, перпендикулярны? , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2)
, при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) 
 мы сможем найти из условия:
мы сможем найти из условия: 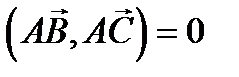 , для этого найдем проекции векторов
, для этого найдем проекции векторов  и
и  на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора
на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора 
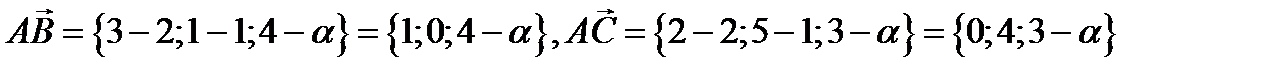

 Итак: векторы
Итак: векторы  и
и  перпендикулярны при
перпендикулярны при  и при
и при 

 ;
; ;
; ;
; ;
; ;
; ;
;
 где скалярное произведение векторов вычисляется по формуле:
где скалярное произведение векторов вычисляется по формуле:  где
где  и длина вектора:
и длина вектора:  итак ,в нашем случае, формула принимает вид:
итак ,в нашем случае, формула принимает вид: 
 для нахождения
для нахождения  необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:
необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:

 пр
пр  ;
; , для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:
, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:

 ;
;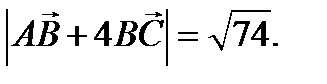
 в нашем случае формула принимает вид:
в нашем случае формула принимает вид: 
 находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:
находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:

 Итак
Итак 
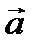 определяется углами
определяется углами  , образованными им с осями координат
, образованными им с осями координат  Косинусы этих углов (направляющие косинусы вектора) определяются по формулам:
Косинусы этих углов (направляющие косинусы вектора) определяются по формулам:  Направляющие косинусы вектора связаны соотношением
Направляющие косинусы вектора связаны соотношением  мы имеем вектор единичной длины, такой вектор называется ортом
мы имеем вектор единичной длины, такой вектор называется ортом  для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину
для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину 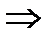

 орт вектора
орт вектора  .
.
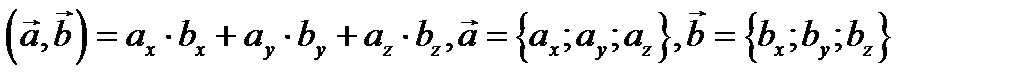 (см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :
(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :

 , где
, где 


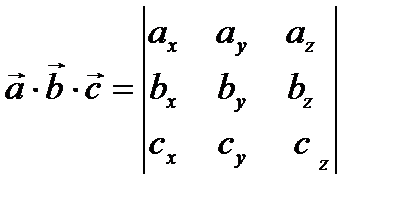 , где
, где 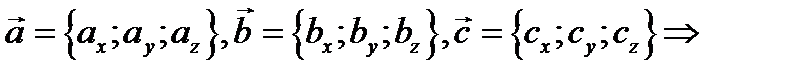
 Итак:
Итак: 
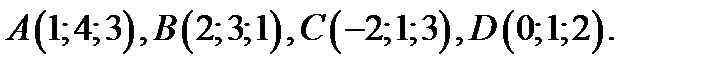
 ;
; ;
; объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения
объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения  объем
объем

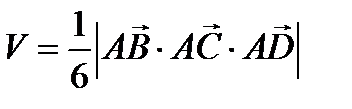
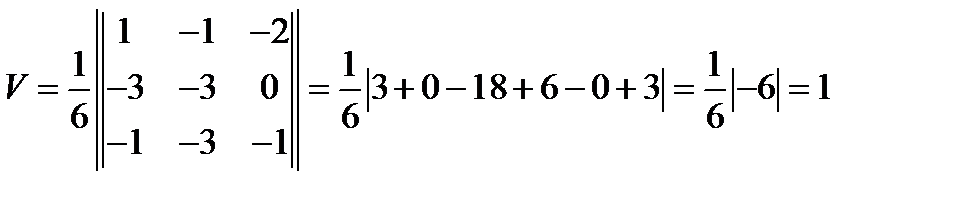 ;
;
 ; (смотри пункт 5,3)
; (смотри пункт 5,3) вычисляется по формуле:
вычисляется по формуле: так как грань
так как грань 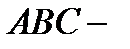 треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения
треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения  найдем проекции векторов на оси координат:
найдем проекции векторов на оси координат:



 ;
;