III Расчет процентилей и доверительных границ к ним

При анализе распределений случайных величин также можно обращать внимание на величины x, при которых функция распределения F_x(x) принимает определенные значения.

Наиболее «популярна» из этих значений медиана Me, для которой F_x(Me)=1/2. То есть можно сказать, что в половине случаев случайная величина принимает значения, большие медианы, а в половине случаев – меньше медианы.

Медиана является частным случаем процентиля случайной величины. Если p – некоторая вероятность, то есть число в пределах от 0 до 1, то процентиль Pr_x(p)=x должен обладать свойством F_x(x)=p.

Частным случаем процентилей являются децили (9 чисел, делящих наблюдения на равные по встречаемости части, то есть процентили при p=0,1, 0,2, … 0,9) и квартили (3 числа, делящие наблюдения на равные по встречаемости части, то есть процентили с р=0,25, 0,5 и 0,75). Соответственно пятый дециль и второй квартиль являются медианой.

Рассчитать величину медианы и других процентилей можно из таблицы частот, ориентируясь на частоту нарастающим итогом.

Выполним команду Analyze / Descriptive statistics / Frequencies и выберем переменную vozrast:

VOZRAST

Видно, что 48,1% имеют возраст 46 лет или менее, а 50,5% - возраст 47 или менее. Следовательно, значение медианы должно быть где-то между 46 и 47, примерно равное 46,8 лет.

При этом первый квартиль – примерно 37 лет, а третий – примерно 59 лет.

Однако при сравнении медиан и других процентилей нужно также помнить, что они, как и все другое, определяются со статистическими погрешностями.

Эта задача близка к задаче определения доверительных границ к биномиальному распределению, но не совпадает с ней, так как там мы определяли, какая вероятность может быть у случайной величины, у которой мы знаем частоту. Здесь же мы знаем вероятность (по которой определяется процентиль), и наша задача – определить, в каких пределах может колебаться частота.

Этот расчет затабулирован в Excel, для него имеется функция КРИТБИНОМ (критические точки биномиального распределения).

Определим 95%-ные доверительные границы для 25%-ной квартили возраста. Внесем исходные данные в таблицу Excel:

Рассчитаем ранг процентиля, то есть номер этой величины в порядке нумерации значений по возрастанию:

Рассчитаем нижнюю доверительную границу для ранга. Для этого вызовем мастера функций и в груме «Статистические» найдем функцию КРИТБИНОМ:

В качестве числа испытаний берется число наблюдений. В качестве вероятности успеха – вероятность, для которой рассчитывается процентиль.

Функция КРИТБИНОМ рассчитывает величину x, при которой для случайной величины x, распределенной биномиально с указанными числом испытаний и вероятностью успеха, выполняется условие P(x£x)=a. Ну, или если точнее, что при уменьшении x на единицу уменьшается до значения, меньших a, так как биномиальное распределение – дискретное, и для нее функция распределения – кусочно-постоянная с шагом единица, «рваная», так что для произвольной вероятности a найти x, такое, что для него в точности выполнялось бы равенство P(x£x)=a, нельзя.

Однако мы строим доверительный интервал с указанным р, поэтому нам надо «отщипнуть» с обоих сторон по р/2. Поэтому для расчета нижней границы берем a=р/2.

Аналогично для расчета верхней доверительной границы возьмем a=1-р/2.

Таким образом, ранг первого квартиля равен 145,5 (то есть квартиль - полусумма 145-го и 146-го значения в порядке возрастания), но квартиль с р=0,05 может принимать значения в пределах от величины с 125-ым рангом до величины со 166-ым рангом.

По приведенной выше таблице нам удобнее работать не с рангами, а с частотами, поэтому пересчитаем доверительные границы рангов в частоты:

Итак, для квартиля 0,25 соответствующие частоты – от 0,215 до 0,285.

По приведенной выше таблице частот переведем их в возраста. Скопирую таблицу частот еще раз, удалив неактуальные куски:

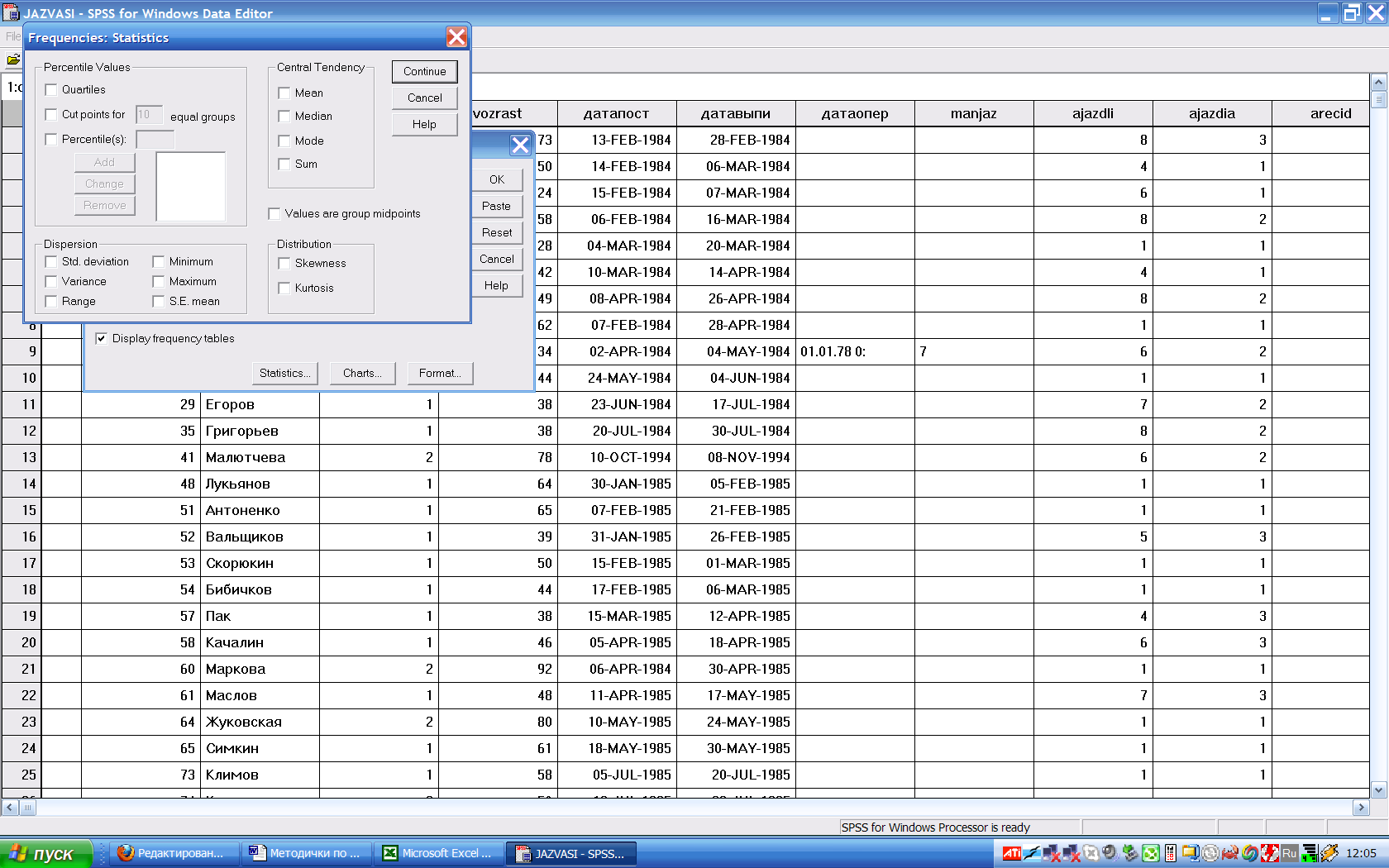
Частоте 21,5% соответствует возраст 35,2 года, частоте 25% - возраст 36,9 года, и частоте 28,5% - возраст 38,3 года. Следовательно, квартиль равна 36,9, а ее доверительные границы – от 35,2 до 38,3.

Если использовать полученные величины для построения графика с «полосами погрешность», то «погрешность -» будет равна 1,7, а «погрешность +» будет равна 2,1.

Рассчитывать процентили можно также и в самом SPSS. для этого нужно после выполнения команды Analize / Descriptive Statistics / Frequencies и выбора переменной нужно нажать на кнопку «Statistics»:

Выбор вариантов расчета процентилей – в верхнем левом углу, хотя расчет медианы можно отметить и в группе «Общая тенденция».

Вариант «Cut points for…» позволяет «разрезать» случаи на указанное количество групп одинаковой численности. Например, при выборе 10 групп будут рассчитаны децили.

Если нужно вводить какие-то конкретные значения, то надо поставить «галочку» на «Percentile(s)», после чего активизируется окошко для ввода числа и кнопка «Add» для его добавления.

Числа надо вводить через точку и как проценты. Для рассмотренного выше случая отметить расчет квартилей и добавим 0,21477663 и 0,285223368 как ее доверительные границы:

В результате получим следующую таблицу:

Statistics

VOZRAST

Видно, что SPSS не интерполирует значения процентилей, выдавая наиболее подходящую величину, а не промежуточное значение. Для рассмотренного случая, когда статистические погрешности близки к единице, такое округление слишком грубо, поэтому лучше пользоваться значениями, проинтерполированными самостоятельно.

Рассмотрим еще два технических приема, полезных при анализе рангов.

· Во-первых, значение ранга можно вычислить и сохранить в качестве новой переменной. Это делается командой Transform / Rank cases, после чего надо выбрать нужную переменную. В результате будет добавлена новая переменная, имя которое получается прибавлением буквы r к имени исходной переменной, а в этикетке будет написано, что это – ранг соответствующей переменной.

· Вторым техническим приемом, ускоряющим работу с рангами, является возможность сортировать случаи в порядке возрастания или убывания переменной. Для этого нужно выполнить команду Data / Sort cases, выбрать нужную переменную и порядок сортировки.

После выполнения этой команды строки будут переставлены местами. Для тех, кто привык к определенному порядку, это может быть неудобно – трудно находить случаи. Поэтому желательно иметь переменную, в которой будет сохранен исходный номер по порядку, а по окончанию работы можно будет отсортировать случаи по этой переменной, вернув исходный порядок.

Поиск по сайту: