|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПОЛИТИЧЕСКОГО ПОВЕДЕНИЯ
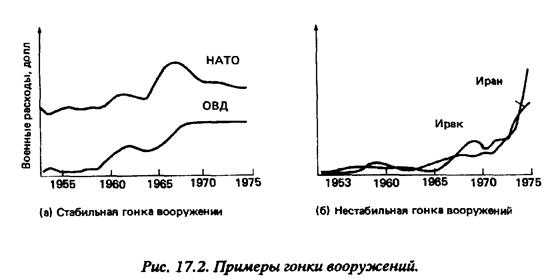
Нижеприведенные примеры отбирались нами так, чтобы лучше очертить границы применения математических моделей политического поведения, а также чтобы познакомить читателя с наиболее распространенными моделями. В каждом из этих примеров обсуждается только часть возможных следствий модели, поскольку каждой модели посвящены без преувеличения сотни исследований. Пример 1. Гонка вооружений (модель Ричардсона) В 1918 г. английский метеоролог Льюис Ф. Ричардсон, служивший на фронте санитаром, вернулся с первой мировой войны потрясенный размерами виденных им разрушений и насилия. Он был преисполнен решимости применить свои недюжинные математические способности и новейшие научные знания к изучению феномена войны. Поскольку первой мировой войне предшествовала гонка вооружений, Ричардсон обратился к рассмотрению этого явления. Благодаря своим занятиям физикой он был хорошо знаком с дифференциальным исчислением, используемым при моделировании динамических процессов. Гонка вооружений, рассуждал он, тоже является [c.481]динамическим процессом и может быть приблизительно описана с помощью математической модели.[c.482] Испробовав десятки сложных математических формул, Ричардсон, в конце концов, остановился на относительно простой модели, учитывающей действие всего лишь трех факторов. Первый из них состоит в том, что государство Х ощущает наличие военной угрозы со стороны противника – государства Y. Чем большим количеством вооружений располагает Y, тем больше вооружений захочет приобрести X в ответ на воспринимаемую им угрозу. Однако в то же самое время государство Х вынуждено решать и насущные социальные задачи, и не может перевести всю свою экономику на рельсы военного производства. Следовательно, чем большим количеством вооружений располагает X, тем меньше дополнительных вооружений оно сможет приобрести из-за существующего бремени расходов. И, наконец, по рассуждению Ричардсона, существуют и прошлые обиды, влияющие на общий уровень вооружений. Та же самая логика, которая применима к государству X, действует и в отношении государства Y, для которого составляется сходное уравнение. С математической точки зрения все это рассуждение сводится к двум уравнениям: Xt+1 = kYt – aXt + g, Члены уравнений Xt и Yt обозначают величины уровней вооружений в момент времени t, Xt+1 и Yt+1 – в момент времени t+1. Коэффициенты k, т, а и b все являются положительными величинами, a g и h – положительными или отрицательными в зависимости от того, насколько в целом враждебно или дружественно настроены государства X и Y по отношению друг к другу. Величина угрозы отражена в членах kYt и mXt, поскольку, чем больше эти числа, тем больше количество вооружений у противной стороны. Величина расходов отражена в членах – aXt и bYt, поскольку за счет этих членов снижается уровень вооружений в следующем году. Наконец, константы g и h отражают величину прошлой обиды, которая в рамках данной модели считается неизменной. Красота модели Ричардсона заключается в ее автономности: если вам известны значения коэффициентов и уровни вооружений государств Х и Y в одном каком-то [c.482]году, вы можете с помощью этой модели предсказать величину уровня вооружений в любом последующем году. Это придает модели способность – во всяком случае, в теории – прогнозировать будущее, и Ричардсон надеялся, что если политики смогут предсказывать приближение войны, то они смогут научиться и предотвращать ее. На удивление оригинальная работа Ричардсона пребывала в безвестности в течение ряда десятилетий. Он продолжал свои исследования в области математизации международных отношений вплоть до самой пенсии, но работа его не получила признания ни в научных, ни в политических кругах. Ричардсон умер в 1953 г., будучи хорошо известен своими работами по математической метеорологии, но совершенно неизвестен в области политической науки. Второе рождение работы Ричардсона наступило после того, как в конце 50-х годов ее обнаружила и стала всячески рекламировать группа социологов из Чикагского и Мичиганского университетов. Журнал “Journal of Conflict Resolution” посвятил Ричардсону целый выпуск. Были опубликованы две рукописи Ричардсона – “Статистика непримиримых распрей” и “Вооружение и отсутствие безопасности”, – и его модель стала краеугольным камнем новой области знаний – математической теории международных отношений. К началу 70-х годов модель была испробована уже сотни раз на самых разных вариантах гонки вооружений. Модель работала! Не идеально, конечно: ведь любая гонка вооружений имеет сложный комплекс причин, совокупность которых не в состоянии охватить ни одна искусственная модель. Однако модель Ричардсона в целом эффективна в случаях краткосрочных прогнозов, и – что существенно – лучше нее не работает никакая другая автономная модель. Касается ли это противостояния между НАТО и Организацией Варшавского Договора, ближневосточного конфликта или трагической 30-летней войны в Юго-Восточной Азии, модель Ричардсона гонки вооружений всякий раз адекватно отражает основные особенности конкретного варианта гонки вооружений. При этом эмпирически обнаружилась еще одна область применения данной модели. Одной из важнейших характеристик модели Ричардсона является стабильность. В простейшей форме стабильность [c.483]определяется тем, какими – ускоренными или замедленными – темпами развивается гонка вооружений3. На рис. 17.2. показаны два примера гонки вооружений: стабильной гонки вооружений между странами НАТО и ОВД и нестабильной между Ираном и Ираком; на обеих схемах размеры военных расходов приведены согласно данным ежегодников Международного института мирных исследований в Стокгольме (SIPRI). В случае нестабильной гонки вооружений, проблема предотвращения войны была, конечно, тем главным стимулом, который с самого начала подтолкнул Ричардсона к его разработкам. Оказалось, что его модель умеет очень хорошо предсказывать войну, поскольку почти всем современным войнам предшествует нестабильная гонка вооружений. Ричардсон постулировал это в своей основополагающей работе, а впоследствии это было подтверждено другими, более систематическими исследованиями.
В конце 70-х годов Майкл Уоллес обнаружил, что нестабильность гонки вооружений тесно коррелирует с войной. Используя несколько более сложное, однако, основанное на Ричардсоновой модели определение гонки вооружений, Уоллес обнаружил, что из 28 серьезных международных конфликтов, сопровождавшихся гонкой вооружений [c.484]в период с 1816 по 1965 г., целых 23 завершились войной. А из 71 конфликта, не вовлекавшего гонки вооружений, только три перешли в войну. Другой иллюстрацией того же положения может служить следующий пример. В 1976 г. У. Лэдд Холлист, опираясь на модель Ричардсона и данные SIPRI о военных расходах, изучал четыре случая гонки вооружений: между СССР и США, между Индией и Пакистаном, между Ираном и Ираком и между Израилем и Египтом в период с 1948 по 1973 г. Из всех четырех случаев стабильной была только гонка СССР – США, что представляло своего рода проблему, и вот почему. Ведь гонки Индия – Пакистан и Израиль – Египет, будучи нестабильными, закончились войной, как и предсказывала модель; гонка СССР – США, будучи стабильной, не перешла в войну опять же в соответствии с предсказанием модели. Однако между Ираном и Ираком велась нестабильная гонка вооружений, а войны не было. Эта неувязка разрешилась в 1980 г., четыре года спустя после публикации статьи Холлиста, когда долго тлевший конфликт между Ираном и Ираком, наконец, разразился войной. Ирано-иракская гонка вооружений была стабильной до конца 60-х годов и лишь в 70-х годах превратилась в нестабильную, что дополнительно сужает тот период времени, когда, согласно предсказанию, могла случиться война. Модель Ричардсона – это только один из представителей очень большого классадинамических моделей, т.е. таких, которые моделируют развитие некоторого процесса во времени. Многие из этих моделей реализуются в виде дифференциальных уравнений, а многие заимствуют математический аппарат из моделей демографического роста и других биологических процессов. Еще более сложными являются динамическиекомпьютерные имитационные модели, которые моделируют сложные процессы с помощью больших систем уравнений, не поддающихся решению алгебраическими средствами. Объектами компьютерных имитационных моделей зачастую являются целые государства или глобальные политические и экономические системы, и эти модели все чаще используются для проигрывания сценариев типа “что будет, если…”, затрагивающих различные сюжеты внутренней и международной политики. [c.485] До недавнего времени большинство динамических моделей, изучавшихся в политологии, отражали систематические, “правильные” процессы. В последнее десятилетие значительная работа проделана по“хаотическим моделям”, которые являются более сложными, чем модель Ричардсона и не имеют случайных компонентов, но во временном отношении генерируют поведение, которое кажется случайным. Динамический хаос может служить объяснением того, как постоянный политический процесс порождает в высшей степени нестандартное, “неправильное” поведение, например, гражданскую войну или парламентскую нестабильность. Пример 2. Игра “дилемма заключенного” Одна из наиболее развитых областей математического моделирования социального поведения называется теорией игр. “Игры” в рамках данной теории – это ситуации, в которых два (или более) участника делают выбор в отношении своих действий и выигрыш каждого участника зависит от совместного выбора обоих (всех). Примерами этого типа ситуаций могут служить такие традиционные игры, как шахматы, покер и футбол, поскольку исход их зависит от совокупных действий игроков. Игры, изучаемые теорией игр, обычно более формализованы, чем традиционные, и вознаграждения в них представляют собой не просто выигрыш или проигрыш, а нечто более сложное, но принцип соревнования и здесь и там один и тот же. Теория игр была разработана во время второй мировой войны и изначально рассматривалась как секретное оружие, однако с той поры она давно превратилась в самостоятельную отрасль математики. Теория игр первоначально разрабатывалась на материале одного из типов соревнования, который носит название игры с нулевой суммой и заключается в том, что, сколько один игрок выигрывает, столько же другой проигрывает. К этой категории принадлежит большинство обычных игр, а также некоторые из “игр”, с которыми мы встречаемся в области политики, например выборы. Однако большая часть политических ситуаций являются играми с ненулевой суммой, или кооперативными, когда оба игрока при определенных условиях могут [c.486]оказаться в выигрыше (т.е. тот факт, что один из игроков выиграл, вовсе не означает, что другой столько же проиграл). Из кооперативных игр лучше всего изучена игра “дилемма заключенного”, вариант которой разбирается ниже. Представим себе ситуацию позиционной войны во время первой мировой войны. Солдаты британских и германских войск сидят в окопах друг против друга, разделенные только нейтральной полосой, а снайперы на брустверах выжидают, когда какой-нибудь неосторожный солдат встанет на секунду во весь рост в обстреливаемом месте, чтобы убить его. В самом начале подобного патового положения потери обеих сторон от снайперских выстрелов велики, и обе стороны чувствуют себя скованно и неуютно, будучи полностью привязанными к окопам. Но со временем, когда одни и те же подразделения неделю за неделей привыкают друг к другу, урон от снайперских атак начинает сходить на нет, постепенно приобретая характер просто несчастного случая. Посторонние наблюдатели, посещающие линию фронта, бывают удивлены, видя, как с обеих сторон солдаты расхаживают не таясь, совершенно без всякого прикрытия и никто никого не пытается при этом убить. Это совсем непохоже на то, как изображают войну в кино, и такое положение бесит некоторых офицеров, но “сотрудничество” становится правилом, и те неопытные офицеры, которые стараются заставить солдат нарушить это правило, имеют скверное свойство погибать от несчастного случая. Надо заметить, что подобное неформальное перемирие происходит без каких-либо открытых договоренностей между враждующими сторонами. Вышеописанное представляет собой вовсе не плод выдумки пацифиста, а реальную ситуацию. Роберт Аксельрод приводит такую цитату из мемуаров британского офицера, участвовавшего в первой мировой войне: “Я пил чай в компании, когда мы услышали крики и вышли наружу узнать, в чем дело. Мы увидели, как германские и наши солдаты стоят друг против друга на своих брустверах. Внезапно рядом разорвался снаряд, но не причинил никому вреда. Естественно, обе стороны поспрыгивали в окопы, и наши стали ругать немцев, и вдруг один смелый немец вскочил на бруствер и крикнул: "Нам очень жаль, мы надеемся, никто не пострадал. Это не наша вина, это проклятая прусская артиллерия!"”4. Это явление может быть объяснено с помощью очень широко применяемой модели под названием игра [c.487]“дилемма заключенного”. В “дилемме заключенного” обе стороны стоят перед выбором: либо сотрудничать друг с другом, либо друг друга обманывать. В том примере, который мы привели, платежная матрица (в терминах количества человек, убиваемых ежедневно) могла бы выглядеть так, как это показано в табл. 17.1. В этой матрице выплаты приводятся в таком порядке: британская сторона, германская сторона – и обозначают среднее число солдат, убиваемых за день. Таблица 17.1
Стратегия сотрудничества означает отсутствие намеренных попыток убить солдата противной стороны; стратегия обмана означает наличие таких попыток. Если обе стороны сотрудничают (клетка 1), то мы принимаем потери за величину случайную, что в среднем может выражаться в гибели одного солдата в день с каждой стороны. Если обе стороны намеренно ведут снайперский отстрел (клетка 4), то смертей будет больше, но ненамного, потому что обе стороны будут укрываться в окопах и не станут выставляться в качестве мишеней. И, наконец, если одна сторона начинает вести снайперский отстрел, в то время как другая занимается сотрудничеством (клетки 2 и 3), то та сторона, которая пытается сотрудничать, понесет значительные потери, а другая предположительно будет готова к отпору и вообще не понесет потерь в этот день. В “дилемме заключенного” интересно то, что, чем хуже каждая из сторон думает о другой, тем скорее обе они примут стратегию обмана. Если одна из сторон выбирает сотрудничество, то наихудший исход (10 смертей) может ожидаться тогда, когда другая сторона в ответ выберет обман. Если одна из сторон выбирает обман, то неблагоприятный исход ожидается и тогда, когда другая сторона так же выберет обман, но это приведет всего лишь к трем смертям. Поэтому если выбирать из худших исходов [c.488]наилучший (это называется минимаксным решением), то надо обманывать. Но при этом следует учитывать, что если бы обе стороны сотрудничали, то обе они были бы в большем выигрыше, нежели в случае взаимного обмана (то есть теряли бы каждая по одному солдату в день). В этом заключается дилемма выбора. Приведенный пример – это всего лишь один случай из очень большого числа ситуаций, к которым применима игра “дилемма заключенного”5. Другие стандартные примеры – это: обоюдный контроль над вооружениями, контроль за выполнением деловых контрактов, взаимный контроль государства и фермеров за ценами на продовольствие, соблюдение картельных соглашений, принятие решения о начале войны обычного типа и даже совместное решение студентов не готовиться особенно усердно к экзамену (поскольку требования, предъявляемые к отдельному ответу, обычно зависят от общего уровня ответов). В отношении “дилеммы заключенного” наиболее интригующим представляется то обстоятельство, что в реальной действительности игроки чаще выбирают сотрудничество, несмотря на все факторы, подталкивающие их к обману. Для специалиста по теории игр вопрос заключается в том, почему так происходит. Вопрос этот становится особенно интересным, если учесть, что, согласно существующим исследованиям по играм с ненулевой суммой, наиболее соблазнительными для игроков свойствами обладает минимаксное решение (предполагающее обоюдный обман). В этой связи до недавнего времени оставалось неясным, каков, собственно, механизм сотрудничества (кооперации) в “дилемме заключенного”. Ключ к решению этой проблемы лежит, по-видимому, в том, что игра носит итеративный характер – т.е. повторяется много раз, – что позволяет каждой из сторон многократно наказывать другую за обман. В серии весьма искусных опытов, проведенных в начале 80-х годов, Роберт Аксельрод показал, что простая стратегия игры “зуб за зуб” – т.е. причинение противнику всего того, что он причинил вам в предыдущем туре игры, – оказывается предпочтительной в ситуации, когда большое число игроков занято в играх типа “дилеммы заключенного”. В частности, если из двух игроков оба руководствуются стратегией “зуб за зуб”, то, начав игру с сотрудничества, они и далее [c.489]будут продолжать в том же духе. Если игрок, следующий стратегии “зуб за зуб”, встречается с игроком, склонным к обману, то это, скорее всего, приведет ких взаимному уничтожению. Следовательно, в реальной действительности, где распространены ситуации типа “дилемма заключенного”, наиболее удачливыми окажутся, скорее всего, те игроки, которые согласны сотрудничать по принципу “зуб за зуб”. В тех ситуациях, в которых не умеющие или не желающие сотрудничать игроки имеют мало шансов на выживание (как в описанной выше позиционной войне или в выполнении условий деловых контрактов), успех будет, в конечном счете, на стороне того игрока, действующего по принципу “зуб за зуб”, с которым сотрудничать вполне безопасно. Это во многом объясняет, почему сотрудничество реально существует в мире, где нет ни принуждения к выполнению контрактов, ни договоренностей между игроками и где противника, пытающегося сотрудничать, выгодно обмануть. Приведенный пример всего лишь в общих чертах дает представление об исследованиях Аксельрода и др. и о той обширной литературе, которая посвящена игре “дилемма заключенного”. Небольшие видоизменения в этой игре позволяют, кроме всего прочего, исследовать такие проблемы, как вопрос об осмысленности применения угроз, о преимуществах, которые можно получить от прерывания сделки или переговоров (стратегия “сжигания мостов”), о важности блефования и отвлекающих маневров, о значимости случайного поведения, а также целый ряд других характерных особенностей ситуаций состязания. Пример 3. Модель Даунса В начале работы сессии конгресса 99-го созыва в январе 1985 г. к присяге при вступлении в должность были приведены только 434 члена палаты представителей вместо обычных 435. Одно место по 8-му избирательному округу штата Индиана оставалось незанятым ввиду того, что ситуация, сложившаяся в предвыборной борьбе между кандидатом от демократов преподобным Фрэнсисом Макклоски и его соперником-республиканцем Ричардом Ф. Макинтайром, была близка к патовой. Согласно первоначальному подсчету, Макклоски обошел соперника только на 72 голоса (из 233 тыс. поданных бюллетеней), т.е. на [c.490]0,03%. Окончательный подсчет, предпринятый палатой и послуживший причиной демонстративного ухода с заседания одного из депутатов-республиканцев, показал отрыв в пользу Макклоски уже только в четыре голоса, т.е. 0,0017% всех поданных голосов. Чтобы представить этот случай в истинном свете, зададимся вопросом, какова вероятность того, что 233 тыс. избирателей, каждый из которых должен опустить в избирательную урну зеленый или красный бюллетень, сделают свой выбор так, что окончательное соотношение бюллетеней разного цвета в урне лишь на 0,03% отклонится от идеального разбиения 50:50? Даже если допустить, что всем избирателям одинаково безразлично, какого цвета бюллетень опустить в урну, – эта вероятность не превышает 0,0005 (огрубленно 1 шанс из 2000). Поэтому выборы, приближающиеся по результатам к игре вничью, следовало бы расценивать как крайне маловероятное событие. И, однако, в американской избирательной системе они совсем не так уж редки. Например, из семи президентских выборов три закончились с перевесом одного претендента над другим менее чем в 2% общего числа поданных голосов.
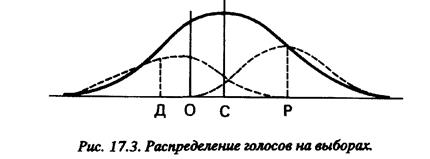
К этому можно было бы добавить много других примеров, относящихся к выборам в конгресс, в органы власти штатов и округов. С точки зрения разработчика математических моделей, это довольно загадочное явление: почему столько результатов выборов оказываются между собой намного ближе, чем ожидалось бы даже при случайном распределении? В одной из своих работ по формальному моделированию в политологии Энтони Даунс предложил простой механизм объяснения этого феномена. [c.491] Даунс использовал модель, впервые предложенную Хэролдом Хотеллингом в 1929 г. для объяснения того, почему бакалейные лавки в провинциальных городках, как правило, располагаются вблизи друг от друга. В качестве примера в рамках базовой модели Хотеллинга возьмем следующий. Допустим, что городок представляет собой шахтерский поселок в глубокой провинции, а ближайший магазин расположен от него в 50 милях. В поселок приезжают, чтобы открыть в нем магазины, два торговца-конкурента. Из опыта торговли в шахтерских поселках оба они одинаково хорошо знают, какие товары будут здесь пользоваться спросом, поэтому единственное, чем их магазины могут различаться, – это месторасположение, потому что клиенты-шахтеры, очевидно, предпочтут посещать тот магазин, который находится ближе. В подобном случае существует только одно место, идеально подходящее для расположения магазина, – это точка, в которой среднее расстояние от дома каждого шахтера до магазина является минимальным. Если оба владельца магазинов это осознают, то они расположат свои лавки в одном и том же месте, несмотря на то, что они окажутся впритык друг к другу, и, добавим мы, несмотря на то, что расположение лавок вдали друг от друга сократило бы время, необходимое части клиентов, чтобы дойти от дома до лавки, и притом сохранило бы возможность для владельцев лавок поровну поделить между собой объем коммерции (кстати сказать, это последнее соображение являет собой еще один пример “дилеммы заключенного”). Логику модели Хотеллинга Даунс применил к ситуации выборов. В простейшей модели Даунса предполагается, что избиратели упорядочены соответственно своим политическим мнениям – от либералов до консерваторов (как показано на рис. 17.3). Предполагается также, что каждый избиратель будет голосовать за того кандидата, который идеологически ему ближе. В подобной ситуации кандидаты будут стремиться быть идеологически как можно ближе к “золотой середине” (точка, помеченная на рисунке буквой С). Если один кандидат займет центристскую позицию (точка С), а другой кандидат займет позицию, отличную от центристской (скажем, соответствующую точке О), то последний проиграет на выборах: ведь за кандидата, занимающего точку С, проголосует более 50% [c.492]избирателей, расположенных вправо от С, затем голоса распределятся в промежутке от С до О и, таким образом, это будет означать победу данного кандидата на выборах. Это саморегулирующийся процесс: кандидат может его проигнорировать, но только ценой своего провала на выборах. Поэтому следует думать, что опытные политики – те, которые уже неоднократно одерживали победу на выборах, – обладают способностью вычислять или угадывать, где расположена политическая “золотая середина”.
Эта модель объясняет то важное наблюдение, что на многих выборах голоса разбиваются почти пополам: ведь опытные кандидаты будут стараться быть как можно ближе к центру голосования. Однако модель Даунса предсказывает, что у кандидатов при этом будут почти одинаковые позиции, а это вовсе не обязательно так. Кандидаты на выборах в США по большей части очень близки идеологически, но все же редко настолько близки, насколько это предполагается данной моделью. Поэтому надо посмотреть, не нуждается ли модель в каких-то дополнительных допущениях. К этой проблеме можно подходить с разных сторон, но простое наблюдение свидетельствует о том, что в большинстве округов каждый кандидат должен пройти два тура выборов – первичный и всеобщий. На первичных выборах распределение идеологических акцентов отклоняется от точки центра. Пунктирные линии на рис. 17.3 показывают гипотетическое распределение голосов в первичных турах отдельно республиканской и отдельно демократической партии: голоса на республиканских первичных выборах обычно сдвинуты сильно вправо, а на демократических – сильно влево, притом, что многие центристски настроенные избиратели в первичных турах вообще не участвуют. Применяя к первичному туру модель [c.493]Даунса – Хотеллинга, мы видим, что для того, чтобы победить, каждый кандидат будет стремиться занять позицию в центре голосов, отданных его партии (на рисунке – точки Д и Р), и тем самым удалится от точки С. Если бы избиратели не придавали значения постоянству позиции кандидата, то самым логичным для каждого кандидата было бы во время первичных выборов занимать позицию партийного центра, а затем немедленно переориентироваться, заняв точку общеэлекторатного центра С. Однако избиратели не столь забывчивы, поэтому кандидатам приходится, двигаясь в сторону центра, не отрываться и от своей первоначальной позиции, чтобы их не обвинили в неустойчивости взглядов. Более того, в том случае, если позиция партийного центра и позиция общеэлекторатного центра разделены значительным расстоянием, кандидат, избранный на первичных выборах, может оказаться просто не в состоянии занять выигрышную позицию на всеобщих выборах и проиграет с большим отрывом от соперника (как это случилось, например, с Барри Голдуотером в 1964 г. и с Джорджем Макговерном в 1972 г.). Но в ситуации, когда оба кандидата изначально сильно удалены от центра, они вполне могут расщепить итоги голосования почти точно надвое, выбрав соответствующие симметрично расположенные относительно точки С, но при этом несовпадающие позиции. Как на то указывает частота выборов с исходом голосования 50:50, американские политики, по-видимому, очень хорошо умеют выбирать именно такие позиции. Представленная здесь модель являет собой всего лишь простейший вариант модели Даунса; и сам Даунс, и другие исследователи занимались разработкой более сложных вариантов, чем этот. В реальной жизни мнения избирателей не поддаются строгому упорядочению в виде колоколообразной кривой, проходящей вдоль единой фиксированной идеологической оси; вместо этого они занимают меняющиеся позиции на целом ряде осей, а по некоторым вопросам занимают сильно отличные друг от друга позиции. Однако даже столь простая модель позволяет объяснить, почему некоторые, но не все выборы кончаются с исходом голосования почти 50:50, почему кандидаты не занимают на всеобщих выборах совпадающих позиций и почему кандидаты часто меняют свои [c.494]идеологические позиции в промежутке между первичными и всеобщими выборами. [c.495] ДРУГИЕ ТИПЫ МОДЕЛЕЙ Приведенные в этой главе примеры могут дать лишь очень поверхностное представление о математических моделях политического поведения. Необходимо также упомянуть, по крайней мере, некоторые другие типы моделей. Существует обширная литература по принятию решений относительно ожидаемой полезности той или иной меры; такое принятие решений является способом моделирования соответствующих ситуаций, сопряженных с риском или неопределенностью. Эти модели очень широко используются в анализе, проводимом в целях выбора той или иной государственной политики. Типичные проблемы, связанные с определением ожидаемой полезности, – это, например, такие: “следует ли строить атомную электростанцию в районе с повышенной сейсмической активностью?”; “сколько песка и соли должно запасти на зиму управление строительства и эксплуатации дорог?”; “следует ли расходовать 1 млн. долларов на спрямление потенциально опасного участка автострады?”. Такие модели часто применяются в политической практике в качестве прескриптивных моделей (помогающих решить, какие меры следует предпринять), но в дескриптивном моделировании (предсказывающем, что люди будут делать на самом деле), они оказываются фактически бесполезными, поскольку большинство индивидов, принимая свои решения, этим моделям не следуют. К моделям ожидаемой полезности близки модели оптимизации, которые по большей части были заимствованы политологией из экономической науки и инженерного дела. Почти всякое рациональное поведение включает в себя процессы своего рода минимизации и максимизации. Для определения оптимального поведения существует целый набор сложных математических приемов, которые показали свою полезность как в случаях “борьбы с природой”, когда в качестве “соперника” выступает непредсказуемое будущее, так и в ситуациях конкуренции с малым числом участников, а кроме того, в условиях рынка, когда обстановка определяется очень большим [c.495]числом участников. Ввиду того, что эти модели детально разработаны и носят весьма общий характер, они представляют собой потенциально мощные средства изучения проблем, связанных с политическим поведением. Совсем новая область математического моделирования имеет дело с компьютерными моделями, связанными с более широкой областью компьютерного моделирования искусственного интеллекта. В то время как большая часть существующих моделей базируется на классических разделах математики – логике, геометрии, алгебре и дифференциальном исчислении, – компьютерные модели основываются на программировании с использованием не уравнений, а алгоритмов (строго сформулированных последовательностей инструкций). Компьютерные модели бывают особенно эффективны при изучении ситуаций, сопряженных с обработкой большого количества информации, например процессов поиска в памяти, обучения, нечисловых процессов. Наиболее употребительной формой компьютерной модели является экспертная система, в которой используется большое количество установок типа “если ... то”. Экспертные системы проявили свои возможности в точном воспроизведении поступков людей в самых разнообразных областях и особенно привлекательны тем, что позволяют моделировать политическое поведение. Компьютерное моделирование является также основным моментом в изучении особо сложных систем, являющихся относительно новой областью. В этих моделях не только уровни переменных изменяются во времени, но также меняются и лежащие в основе математические процессы. [c.496]
Поиск по сайту: |