 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Многокритериальная оптимизация - оптимальный выбор ПО по нескольким критериямСтр 1 из 2Следующая ⇒
Во многих задачах выбора, представляющий практический интерес, бывает трудно, а порой и невозможно свести поиск наилучшего варианта к нахождению оптимума только какого-то единственного критерия качества решения (целевой функции, показателя эффективности, критерия оптимальности). Множественность критериев выбора обусловлена необходимостью учета разнородных характеристик сравниваемых вариантов, разнообразием достигаемых целей. Одним из основных видов дополнительной информации, часто используемым при решении различных многокритериальных задач, является информация о сравнительной важности частных критериев для ЛПР. Обычно такая информация задается в виде числовых коэффициентов важности критериев wk Наиболее известный способ вычисления коэффициента важности критериев это последовательное сравнение критериев по важности. ЛПР упорядочивает все критерии по предпочтительности и каждому критерию приписывает некоторую числовую значимость sk>0. Например, самому важному критерию дается 100 балов, а остальным меньшие баллы в зависимости от их предпочтительности. Важность k-го критерия fk определяется среднеарифметическим значением
wk = sk /
Простейшим способом устранения многокритериальности целей является перевод задачи выбора в русло однокритериальности, например, путем объединения всех частных (локальных) показателей эффективности
f(x) = F(f1(x), f2(x), … , fh(x)) (2)
Подобный прием носит название свертки критериев. Каждый частный критерий отражает какое-то отдельное качество варианта решения. Наилучший варианта должен характеризоваться наиболее удачным сочетанием всех этих отдельных качеств. Таким образом, поиск лучшего варианта решения сводится к отысканию экстремума единственной функции f(x)
X* Î arg
Достаточно популярным способом служит запись глобального критерия в виде суммы локальных критериев (так называемая аддитивная свертка).
f(x) =
или в виде их произведения (мультипликативная свертка)
f(x) =
Существенным недостатком указанных способов свертки критериев является равная важность или значимость критериев для ЛПР, при которой низкие оценки по одним критериям можно компенсировать только за счет высоких оценок по другим критериям. В следствие этого лучшим может оказаться вариант решения, сочетающий не самые лучшие критериальные оценки. Чтобы избежать такого несоответствия, часто используют взвешенные свертки частных критериев эффективности вида
f(x) = или f(x) =
где Способ свертки частных критериев и значения их весов задаются ЛПР, то есть представителем команды разработки ООО «БухгалтерФон Сервис» и отражают потребности компании и рынка.
Поиск по сайту: |
 0, характеризующих весомость, значимость частных критериев fk. Коэффициенты важности составляют в совокупности весовой вектор w = (w1, … , wh), компоненты которого принято нормировать условием
0, характеризующих весомость, значимость частных критериев fk. Коэффициенты важности составляют в совокупности весовой вектор w = (w1, … , wh), компоненты которого принято нормировать условием  = 1.
= 1. (1)
(1)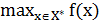 f(x) (3)
f(x) (3) (4)
(4)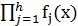 (5)
(5) (6)
(6) , (7)
, (7) - вес частного критерия
- вес частного критерия  .
.