 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Виды и значение показателей вариации
Вариация признака у отдельных единиц изучаемой совокупности различается по размеру. Поэтому важным этапом изучения вариации является её измерение. При характеристике колеблемости признака применяют систему абсолютных и относительных показателей. К абсолютным показателям относятся: 1). Размах вариации (R); 2). Среднее линейное отклонение (d); 3). Дисперсия ( 4). Среднеквадратическое отклонение Эти показатели (кроме дисперсии) измеряются в тех же единицах, что и сам признак: в тоннах, метрах, секундах, рублях. К относительным показателям относятся: 1). Коэффициент осцилляции 2). Линейный коэффициент вариации 3). Простой коэффициент вариации Эти показатели выражаются в процентах или относительных величинах. Размах вариации (R), или размах колебаний, представляет собой разность между максимальным R = Размах вариации измеряется в тех же единицах, что и варианты ряда. На простоту расчёта, этот показатель имеет недостаток – он зависит от двух крайних значений признака, не принимая во внимания вариацию остальных его значений. Среднее линейное отклонение представляет собой среднюю величину из абсолютных отклонений (модулей) значений признака каждой единицы совокупности от средней арифметической. Для несгруппированной совокупности среднелинейное отклонение рассчитывают по формуле средней арифметической простой:
Для сгруппированных данных (вариационного ряда) среднелинейное отклонение определяется по формуле средней арифметической взвешенной:
Дисперсия. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия обозначается буквой ∑ (сигма) в квадрате и равна:
При равенстве весов или когда они равны 1:
Дисперсия является неименованной величиной и обладает рядом математических свойств, некоторые из которых заключаются в следующем: 1) Дисперсия постоянной величины равна нулю; 2) Уменьшение всех значений изучаемого признака 3) Уменьшение всех значений изучаемого признака Дисперсия имеет большое значение в статистическом анализе. Однако её применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. В таких случаях для измерения вариации признака вычисляют среднее квадратическое отклонение. Среднее квадратическое отклонение равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. дисперсии:
А при равенстве весов или когда они равны 1:
Как отмечалось выше, все рассмотрены показатели, за исключением дисперсии, выражаются в единицах измерения варьирующегося признака. Однако это является неудобным при сопоставлении вариации различных признаков. Например, вариация выработки продукции на одного работающего и вариация средней заработной платы будут выражаться, соответственно, в единицах продукции и денежных единицах. Это делает возможным сравнение вариации этих двух показателей. Поэтому для сравнения вариации разных признаков используют относительные показатели вариации. Наиболее распространённым относительным показателем вариации признака выступает коэффициент вариации (V). Он рассчитывается отношением среднего квадратического отклонения в средней арифметической: V= Величина этого коэффициента позволяет оценить интенсивность вариации признака и, следовательно, однородность изучаемой совокупности. Так, при отсутствии вариации, данный показатель равен нулю, а при её увеличении растёт и значение коэффициента вариации. Чем выше его величина, тем больше разброс значений признака вокруг средней и, следовательно, более неоднородна исследуемая совокупность. Если взять отношение среднего линейного отклонения к средней арифметической в процентах, то получим линейный коэффициент вариации.
Отношение размаха вариации к средней арифметической в процентах называется коэффициентом осцилляции:
Поиск по сайту: |
 );
); .
. ;
; ;
; .
. и минимальным
и минимальным  значениями признака в изучаемой совокупности:
значениями признака в изучаемой совокупности:
 =
= 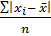 .
. .
. .
. =
=  .
. на одну и ту же величину не изменяет величины дисперсии.
на одну и ту же величину не изменяет величины дисперсии. в одно и то же число раз (k раз) уменьшает величину дисперсии в
в одно и то же число раз (k раз) уменьшает величину дисперсии в  раз.
раз. .
. .
. .
. .
.