 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства неопределенных интеграловСтр 1 из 3Следующая ⇒
Глава 4. Основы интегрального исчисления
Рис.55.
Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования "восстанавливает" функцию, дифференцированием которой получена подынтегральная функция.) Возможно происхождение слова интеграл иное: слово integer означает целый. В ходе переписки Бернулли и Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696г., появилось и название новой ветви математики - интегральное исчисление (calculus integralis), которое ввел И. Бернулли.
Понятие первообразной и неопределенного Интеграла При изучении дифференцирования функций, ставилась задача - по данной функции найти ее производную или дифференциал. Например, если закон движения какого-либо тела задан уравнением вида
где t — время, а S — пройденный телом путь, то дифференцированием функции
этого движения в данный момент времени. Однако в механике гораздо чаще приходится встречаться с обратной задачей: для любого момента времени t дана скорость тела
►Функция F(x) называется первообразнойпо отношению к функции f(x) на некотором множестве X, если на этом множестве функция F(x) дифференцируема и удовлетворяет уравнению F¢(x) = f(x) или, dF(x) = f(x)dx.
Так, например, функция Таким образом, основываясь на знании таблицы производных основных элементарных функций можно составить таблицу.
Таблица базовых первообразных. Таблица№3
Легко проверить, используя правила дифференцирования, что наличие одной первообразной обеспечивает наличие таких функций в бесконечном множестве. Теорема 1.Если данном множестве, то они могут отличаться лишь на посто- янную, т.е. Доказательство: Положим
Действительно На вопрос, как найти все первообразные данной функции, если известна одна из них, дает ответ следующая теорема.
Теорема 2 (о первообразных). Если F(x) - одна из первообразных функции f(x) на заданном множестве, то все ее первообразные имеют вид F(x) + С, где С– произвольная постоянная. Геометрически y = F(x) + C означает, что график любой первообразной функции получается из графика функции y = F(x) простым сдвигом его параллельно оси ОУ на величину С (см. рисунок 56). График первообразной от функции f (x) называется интегральной кривой этой функции, поэтому неопределенный интеграл геометрически представляется множеством всех интегральных кривых, получаемых при непрерывном параллельном движении одной из них по вертикали.
Рис.56.
В связи с тем, что одна и та же функция f(x) имеет бесконечно много первообразных, возникает проблема выбора первообразной, которая решает ту или иную практическую задачу.
Пример 1. Найти первообразные для функции Решение. Множество всех первообразных функции есть 4=2+6+С Искомой первообразной является функция Аналогично через точку М(0; 3) проходит парабола Графически это изображено на рисунке 57.
Рис. 57.
► Совокупность всех первообразных для функции f(x), то есть выраже- ние F(x) + C, где С – произвольная постоянная, называется неопреде- ленным интегралом и обозначается
Теорема 3 (о существовании неопределенного интеграла) Если функция существует первообразная, а значит,иинтеграл · Знак · Функция f(x) называется подынтегральной; · Произведение f(x)dx называется подынтегральным выражением; · F(x) – одна из первообразных; · х – переменная интегрирования; · Процесс нахождения первообразной называется интегрированием. ! Помни: Правильность интегрирования всегда можно проверить дифференцированием результата.
Пример 2. Найти неопределенные интегралы: а) Решение. а) б) Свойства неопределенных интегралов
Свойство 1. интеграла равна подынтегральной функции. Пример: Свойство 2. интеграла равен подынтегральному выражению. Пример:
Свойство 3. Пример: Свойство 4. Пример:
Свойство 5. (аддитивности) Пример:
Свойство 6. (линейности) Пример: Свойство 7.Если Первые три свойства вытекают из определения неопределенного интеграла. Для доказательства свойств 6 и 7 можно продифференцировать левые и правые части по х и использовать свойство 1 неопределенных интегралов и свойства производных. Доказательство свойства 6.
Доказательство свойства 7.
Пример 3. Найти неопределенные интегралы:
а)
Решение. Используя свойства 5, 6 и 7, находим:
а)
б)
Таблица основных неопределенных интегралов Используя таблицу базовых первообразных и на основании второго свойства неопределенного интеграла получим: если dF (x) = f (x)dx , то ∫ f (x)dx = F (x) + C . Например, поскольку d (sin x) = cos xdx , то ∫cos xdx = sin x + C . Применяя аналогичное рассуждение к каждой из формул таблицы дифференциалов, получаем следующую таблицу простейших неопределенных интегралов, которая в высшей математике играет такую же роль, как таблица умножения в арифметике. Таблица основных неопределенных интегралов Таблица №4
Замечание.В таблице основных интегралов предполагалось, что x является независимой переменной. Однако формулы этой таблицы остаются справедливыми и в случае, когда дифференцируемая функция новой переменной t.
Теорема 4. (Об инвариантности формул интегрирования.) Пусть интегрирования и рывную производную. Тогда Доказательство: Из того, что следует Возьмем теперь функцию F (u) = в силу теоремы об инвариантности вида первого дифференциала функции, имеем
Итак, в силу доказанной теоремы, из справедливости формулы ∫ f (x)dx = F (x) + C, следует справедливость формулы ∫ f (u)du = F (u) + C , которая получается из первой формальной заменой x на u . Таким образом, получаем обобщенную таблицу интегралов. Например, будут справедливы формулы: 1. 2. 3.
Многие интегралы, предварительно преобразовав подынтегральное выражение, удается привести именно к такому табличному виду. Так, например,
Поиск по сайту: |
 Интегральное исчисление возникло из потребности создать общий метод разыскания площадей, объемов и центров тяжести. В зародышевой форме такой метод применялся еще Архимедом. Систематическое развитие интегрального исчисления было получено в 17-м веке, в тесной связи с возникшим тогда же дифференциальным исчислением. Символ интеграла (рис.55) введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма).
Интегральное исчисление возникло из потребности создать общий метод разыскания площадей, объемов и центров тяжести. В зародышевой форме такой метод применялся еще Архимедом. Систематическое развитие интегрального исчисления было получено в 17-м веке, в тесной связи с возникшим тогда же дифференциальным исчислением. Символ интеграла (рис.55) введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма).
 ,
,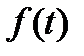 мы находим мгновенную скорость
мы находим мгновенную скорость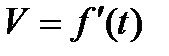
 ; требуется найти закон движения тела, т. е. зависимость пройденного им пути от времени. Как мы можем подойти к решению этой задачи и многих других, которые приводят к постановке обратной задачи - для данной функции f(x) найти такую функцию F(x), производная или дифференциал которой равны соответственно f(x) или f(x)dx? Дадим определение функции F(x).
; требуется найти закон движения тела, т. е. зависимость пройденного им пути от времени. Как мы можем подойти к решению этой задачи и многих других, которые приводят к постановке обратной задачи - для данной функции f(x) найти такую функцию F(x), производная или дифференциал которой равны соответственно f(x) или f(x)dx? Дадим определение функции F(x). – первообразная на любом промежутке по отношению к функции
– первообразная на любом промежутке по отношению к функции  , так как
, так как  . Аналогично из тождества
. Аналогично из тождества  следует, что функция
следует, что функция  является первообразной по отношению к функции
является первообразной по отношению к функции 
 .
.


 , кроме
, кроме 





 , при
, при 







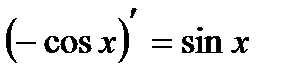









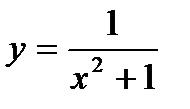





 и
и  – две первообразные для функции
– две первообразные для функции  на
на , где C – постоянная.
, где C – постоянная. .
. , следовательно
, следовательно  .
. .
.
 , проходящие через точки М(2;4) и М(0;3). Сделать рисунок.
, проходящие через точки М(2;4) и М(0;3). Сделать рисунок. , зная, что первообразная проходит через точку М(2;4), подставим ее координаты в предыдущее выражение и найдем С.
, зная, что первообразная проходит через точку М(2;4), подставим ее координаты в предыдущее выражение и найдем С.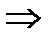 С
С  .
. , геометрически она собой представляет параболу
, геометрически она собой представляет параболу  .
. .
. ,
, непрерывна на данном множестве,то
непрерывна на данном множестве,то .
. называется знаком неопределенного интеграла;
называется знаком неопределенного интеграла; ; б)
; б)  .
. 
 , так как
, так как  ;
;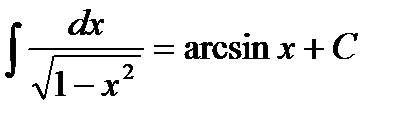 , так как
, так как  .
. , т. е. производная от неопределенного
, т. е. производная от неопределенного
 , т. е. дифференциал от неопределенного
, т. е. дифференциал от неопределенного
 .
.
 .
.
 .
.
 .
.
 , то
, то  .
. .
.

 .
. .
.
 .
. б)
б) 




 (при
(при 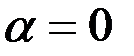 - формула 1 настоящей таблицы);
- формула 1 настоящей таблицы);




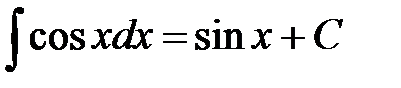

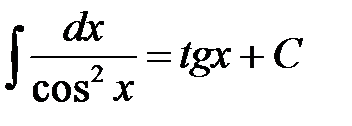


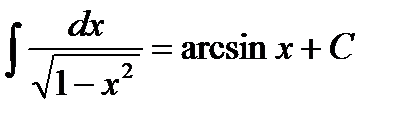



 , где
, где  – любая
– любая – какая-либо известная формула
– какая-либо известная формула – любая функция, имеющая непре-
– любая функция, имеющая непре- .
. , следует
, следует  .
. ; для ее дифференциала,
; для ее дифференциала, отсюда
отсюда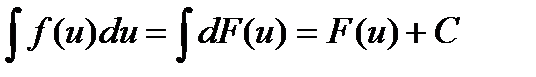
 ;
; ;
; и т.д.
и т.д. , согласно третьей формулы.
, согласно третьей формулы.