 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Векторы в трёхмерной декартовой системе координат
Векторы на координатной плоскости. Принадлежность какой-либо величины к векторным устанавливается опытным путём по тому, подчиняется ли эта величина правилу сложения векторов. Правила сложения и вычитания векторов вы должны были изучать в восьмом классе по геометрии. Освежим в памяти эти правила.
При сложении векторов выполняется переместительное свойство сложения: Правило многоугольника для сложения векторов. При сложении нескольких векторов, их следует расположить так, чтобы начало каждого следующего слагаемого вектора совпадало с концом предыдущего. Суммой векторов будет вектор, проведённый из начала первого к концу последнего из них.
Разность векторов
Исходящая из общего начала векторов Умножение вектора на скаляр. Векторы можно не только складывать и вычитать между собой, но и умножать на скаляр, то есть на величину, характеризующуюся только числовым значением. Умножив вектор Модуль (или длину) вектора обозначают той же буквой, что и сам вектор, но без стрелки. Векторы в трёхмерной декартовой системе координат. Вектор может располагаться не только на плоскости, но и в пространстве. Тогда у точек его начала и конца будет по три координаты, в соответствии с названиями координатных осей: Векторы единичной длины, задающие направления осей Пользуясь правилом сложения векторов и умножения вектора на скаляр, любой вектор
Длина вектора Если два вектора равны между собой, то их проекции также равны между собой. Если все соответствующие проекции векторов равны, то эти вектора равны между собой. Если Проекция геометрической суммы нескольких векторов равна алгебраической сумме проекций слагаемых векторов, то есть, если
Поиск по сайту: |
 Правило сложения векторов.
Правило сложения векторов.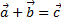
 Чтобы получить сумму векторов
Чтобы получить сумму векторов 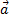 и
и  , нужно совместить начало вектора
, нужно совместить начало вектора  , который и будет равен геометрической сумме векторов
, который и будет равен геометрической сумме векторов 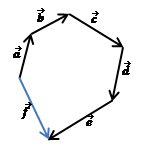 Векторы
Векторы  .
. Разность векторов.
Разность векторов. .
.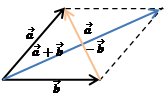 Правило параллелограмма.
Правило параллелограмма.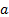 на величину
на величину  , получим вектор
, получим вектор  .
.
 .
. декартовой системы координат называются орты и обозначаются соответственно
декартовой системы координат называются орты и обозначаются соответственно  .
. , где
, где – проекции вектора
– проекции вектора  .
.
 , то
, то  ,
,  и
и 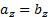 .
. ,
,  и
и 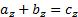 .
.