 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Что такое информация и энтропия?
Как указывалось в § 1.3, главное в порядке – закономерность, предсказуемость физических явлений и процессов. Отсюда очевидно, что количественная оценка порядка должна быть связана с числами, позволяющими установить степень такой предсказуемости. В математике такие числа именуются вероятностью. Ясно, что чем больше вероятность того или иного события, тем больше порядка. И наоборот. Однако непосредственной мерой порядка вероятность в том виде, в котором они введена в соответствующем разделе математики [8, 9, 10], быть не может. Дело в том, что она неточно учитывает динамику изменения порядка в процессах, в которых порядок не постоянен. Приведем такой простой пример. Студент, вернувшись после занятий домой, обнаруживает, что в его комнате беспорядок: не убрана постель. Он убирает постель и устанавливает порядок. Вернувшись на следующий день, обнаруживает вновь беспорядок в своей комнате. Однако на сей раз не только не убрана постель, но и не помыта посуда. Он затрачивает те же усилия, что и накануне, – убирает постель, но порядок не восстанавливает. Мы столкнулись с ситуацией, когда одно и то же изменение беспорядка привело к различному результату. Переводя на язык математики – язык количественных характеристик, – следует признать, что повышая вероятность какого-либо события на одну и ту же величину, мы получаем разный итоговый порядок в зависимости от исходной вероятности этого события. Следовательно, мера порядка I должна определяться не непосредственно, а через свое изменение Δ I :
где р – исходная вероятность указанного события. Получается – мерой порядка является такая величина, изменение которой равно отношению изменения вероятности к исходной вероятности. Из формулы (1.8) следует (после интегрирования): I = lnp. (1.8,а) Иногда удобства ради перед знаком натурального логарифма ставят пересчетный коэффициент: I = a lnp. (1.8,б) Ясно, что качественно появление такого коэффициента ничего не меняет, однако процесс расчета становится более удобным. Тем более, что его можно выбрать самым разнообразным [9] : а=1; тогда единица измерения[нат]; а=1/ln2⇒[бит]; а=1/ln8⇒[байт]; а=2-10/ln8=1/1024•ln8⇒[килобайт]; а=2-20/ln8⇒[мегабайт]; а=2-30/ln8⇒[гигабайт]; а=КБ=1,38∙10-23⇒[Дж/0К]. Коэффициент КБ именуется постоянной Больцмана и чаще всего вводится в формулу (1.8,б) в термодинамике. Величина I именуется информацией [14, 15, 16, 52]. Следует отметить, что поскольку вероятность 0<р≤1, то информация согласно (1.8,б) есть величина отрицательная. Её можно заменить на противоположную по знаку величину S: S = -I = a ln где Р в теории вероятности именуется статистическим весом события (числом возможных вариантов его завершения). Величина S именуется энтропией [1, 6, 8, 14, 16, 44]. Появление двух терминов, характеризующих по сути дела, одно и то же физическое понятие, носит чисто исторический характер. Иногда считают, что энтропия – это мера хаоса, а информация – мера порядка. При этом принимается в расчет, что с ростом энтропии порядок уменьшается, а хаос увеличивается, а рост информации приводит к прямо противоположному результату. Однако ясно, что подобное различие легко снимается простыми приёмами алгебры вещественных чисел. Гораздо более существенным является отнесение термина “энтропия” только к одному разделу науки – термодинамике. Именно здесь этот термин и возник. Дело в том, что термодинамика изучает процессы, которые весьма близки к идеальной (или предельной) модели хаоса. Такой моделью является множество одинаковых хаотически двигающихся шариков (корпускул). Эти шарики в рамках этой модели взаимодействуют друг с другом только путем упругого соударения. Такая модель именуется “идеальный газ” [44]. Казалось бы, вероятность обнаружить в идеальном газе какую-то конкретную частицу практически равна нулю – трудно придумать какую-нибудь величину, с помощью которой их можно различать друг от друга. Однако более тщательный анализ показывает, что это не так. Дело в том, что процентное содержание частиц, обладающих конкретной кинетической энергией, определяется строго детерминированной зависимостью – распределением Больцмана-Максвелла [44]. Таким образом, если бы удалось придумать прибор, улавливающий частицы в миллиардные доли секунды, и задать величину её кинетической энергии, как характерный признак, то число частиц, из которых этот прибор будет её выбирать, значительно меньше общего количества частиц в заданном объёме. Главным параметром, позволяющим производить такой отбор, является температура. В модели “идеальный газ” под температурой подразумевается средняя кинетическая энергия хаотического движения корпускул. Чем выше температура, тем более равномерно распределяется между частицами кинетическая энергия и тем меньше вероятность обнаружения частицы по этому признаку. На рис. 1.2 дано семейство зависимостей вероятности обнаружения частиц с определённой кинетической энергией от самой этой энергии, рассчитанное по формуле Больцмана – Максвелла [44]. Эта зависимость имеет максимум при величине кинетической энергии, соответствующей температуре. Причем, чем выше температура, тем меньше этот максимум. Следовательно, вероятность обнаружения частиц с заданной средней кинетической энергией обратно пропорциональна температуре. Принимая эту вероятность за основу характеристики порядка, можно записать
где Т - температура идеального газа, А – коэффициент пропорциональности. Сопоставляя (1.9,а) с (1.8), получаем
wк.п.д.
Рисунок 1.2. Семейство зависимостей вероятности обнаружения частиц от кинетической энергии хаотического движения частиц:
Обычно коэффициент b принимают равным теплоемкости газа, т.е. коэффициенту пропорциональности между тепловой энергией (суммарной энергией хаотического движения частиц) и температурой. Тогда изменение энтропии записывается в виде
Именно в этом виде энтропия используется в термодинамике. Материал этого параграфа был бы неполным без того, чтобы в мерах энтропии определить понятие закономерности. Рассмотрим какое-нибудь явление природы, например, вращение Земли вокруг Солнца. Интуитивно, или точнее, на основании ранее приобретенных знаний, каждый из нас полагает, что это вращение происходит по замкнутой траектории, весьма близкой к окружности. Эта траектория ежегодно повторяется. Все это так, но с определенной степенью точности. Влияние других планет, метеоритов, космических лучей, процессов на Солнце приводит к тому, что эта траектория соблюдается каждый год с определенной погрешностью. Отклонение от этой средней траектории характеризует степень хаотичности (энтропию) движения Земли. Если расширить это рассмотрение, то нетрудно заметить, что в случае полного хаоса Земля вообще могла летать в космосе по многочисленному количеству самых разнообразных траекторий. В этом случае её энтропия была бы максимальной. Но на самом деле она выбрала лишь чрезвычайно узкую трубку в пространстве вокруг окружности радиусом Rз= 150 млн. км, центр которой совпадает с центром Солнца. Если отложить по оси абсцисс расстояние от центра Солнца, а по оси ординат - вероятность нахождения Земли
Рисунок 1.3. Вероятность удаления Земли от Солнца: а – иллюстративная зависимость; б- фактическая зависимость. рз, то, пренебрегая масштабами, получаем график, данный на рисунке 1.3,а. (Rз – средний радиус орбиты Земли). На самом деле точен рисунок 1.3,б, но неудобен, так как в пределах точности чертежа ничем не отличается от строго детерминированного. Вероятность этой траектории равна практически нулю. Следовательно, энтропия закономерности отрицательна и устремляется в бесконечность. Информация же, наоборот, положительна. Итак, закономерны те явления и объекты природы, энтропия которых стремиться к (-∞). В заключении параграфа следует снова вернуться к сказанному в введении о том, что принятое в информатике и смежных с нею науках понятие информации несколько отличается от начального значения этого слова, которое связано с формированием общественного интеллекта. Расширение области применения термина информация из области процессов интеллектуальной деятельности людей в область процессов природы служит косвенным доказательством того, что разум присущ и природе. Только носителем его служит не отдельный выделенный физический объект, а вся природа в целом. Все процессы в природе, связанные с изменением порядка, именуются информационными (энтропийными).
Поиск по сайту: |
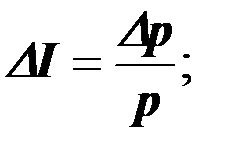 (1.8)
(1.8) = a lnР, (1.8,б)
= a lnР, (1.8,б) (1.9,а)
(1.9,а) (1.9,б)
(1.9,б) - средняя кинетическая энергия хаотического движения молекул.
- средняя кинетическая энергия хаотического движения молекул. (1.9,в)
(1.9,в)