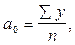|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методичні вказівки і розв’язки типових задачСтр 1 из 7Следующая ⇒
Для статистики характерним є велика кількість чисел, що описують розвиток явищ і процесів у часі. Для аналізу досліджуваних статистичних даних їх потрібно систематизувати, побудувавши хронологічні ряди, які називають рядами динаміки або часовими рядами. В статистиці це - ряди чисел, що характеризують закономірності зміни суспільних явищ і процесів у часі. Кожний ряд динаміки складається з періодів, або моментів часу “t”, до яких належать рівні ряду, та статистичних показників “у”, які характеризують рівні часу. · Залежно від характеру рівнів ряду розрізняють два види рядів динаміки: моментні та інтервальні (періодичні). Моментний ряд динаміки характеризує обсяг явищ на певні моменти часу. Інтервальний ряд динаміки -це числовий ряд, що характеризує розміри суспільних явищ за певні періоди часу. · За кількістю показників, що змінюються, ряди динаміки бувають одновимірні і багатовимірні. Одновимірні ряди динаміки характеризують зміну в часі одного показника. Багатовимірні ряди динаміки характеризують зміну в часі двох, трьох і більше показників. · За повнотою часу динамічні ряди поділяються на повні і неповні. У повних динамічних рядах дати або періоди ідуть один за одним з рівними інтервалами. У неповних динамічних рядах у послідовності показників спостерігають нерівні часові інтервали. · За способом вираження рівнів динамічні ряди поділяються на ряди абсолютних, відноснихісередніх величин. · У динамічних рядах потрібно дотримуватися порівняльності всіх рівнів ряду між собою за територією, колом охоплюваних об’єктів, методом обчислення показників за періодами часу, одиницями величин та іншими параметрами. Завдання статистики полягає в тому, щоб шляхом аналізу рядів динаміки розкрити і охарактеризувати закономірності, що проявляються на різних етапах розвитку того чи іншого явища, виявити тенденції розвитку та їх особливості. · Під час аналізу динаміки обчислюють і використовують такі аналітичні показники динаміки: абсолютний приріст, темп зростання, темп приросту і абсолютне значення одного процента приросту. Абсолютний приріст обчислюють як різниця між поточним і базисним або попереднім рівнем ряду.
де yi - поточний рівень ряду динаміки; y1 - початковий (перший) рівень ряду динаміки; yi-1 - попередній рівень ряду динаміки. Темп зростання обчислюється як відношення зіставлюваного рівня з рівнем, прийнятого за базу зіставлення.
Темп приросту визначають як відношення абсолютного приросту до абсолютного попереднього або початкового рівня, або як різниця між темпом зростання і 1 або 100.
Абсолютне значення одного процента приросту можна знайти шляхом ділення абсолютного приросту на темп приросту за один і той же період, або діленням початкового рівня на 100:
Таблиця 11.1 Розрахунок показників динаміки валового збору картоплі в області за 2000-2005 рр.
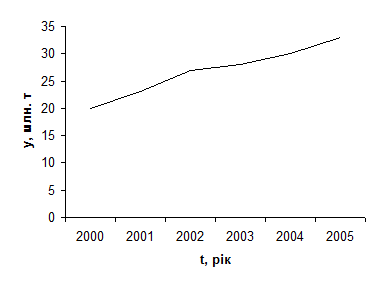
В якості ілюстрації покажемо динаміку валового збору картоплі в області на графіку (мал. 11.1).
Рис.10.1. Динаміка валового збору картоплі в області за 2000 - 2005 рр.
Динамічні ряди складаються з багатьох варіаційних рівнів, а тому вони потребують деяких узагальнювальних характеристик. Для цього обчислюють середні показники: середні рівні ряду, середні абсолютні прирости, середні темпи зростання і приросту. · В інтервальних рядах з рівними інтервалами середній рівень ряду обчислюють за формулою середньої арифметичної простої:
де
n - кількість рівнів. Обчислимо середньорічний рівень валового збору картоплі за шість років:
· Якщо окремі періоди інтервального ряду динаміки мають різну довжину, то для визначення середнього рівня використовують середню арифметичну зважену:
де y - рівні ряду; t - проміжки часу. Наприклад, на 1 січня поточного року на підприємстві за списком нараховували: 1210 працівників; 6 січня прийнято 33 ; 15 січня звільнилось 7 ; 21 січня - прийнято 12 ; 29 січня звільнилося 10 працівників. Середньоспискова чисельність працівників в січні:
· Для наближеної оцінки середнього рівня ряду інколи визначають напівсуму рівнів на початок і кінець періоду:
де уn - кінцевий рівень ряду динаміки. · Якщо моментний ряд динаміки з рівними інтервалами часу між сусідніми датами, то середній рівень визначають за формулою середньої хронологічної:
Розглянемо приклад. Нехай маємо дані про зміну складу тракторного парку в сільських спілках району за перше півріччя поточного року (табл. 11.2). Таблиця 11.2
Визначимо середнє число тракторів за кожний квартал і перше півріччя.
За півріччя середні рівні можна обчислювати за формулою середньої хронологічної або за середньою арифметичною простою із середньоквартальних рівнів.
· Середній абсолютний приріст за даними таблиці 11.1 визначають як середню арифметичну просту з ланцюгових абсолютних приростів:
· Середній темп зростання розраховується за формулою середньої геометричної простої:
де n - число темпів. Середній темп зростання можна обчислити і за іншою формулою:
де yn - кінцевий рівень ряду; y1 - початковий рівень ряду; n - кількість рівнів динамічного ряду. Підставивши значення ланцюгових темпів зростання (табл. 11.1) у формулу середньої геометричної, знайдемо середньорічний темп зростання за певний період часу:
· Середній темп приросту визначають як різницю між середнім темпом зростання і одиницею або 100:
Середньорічний темп приросту валового збору картоплі:
Виявлення основної тенденції (тренду) ряду є одним з головних методів аналізу та узагальнення динамічних рядів. · Одним з найпростіших способів обробки ряду для виявлення закономірності зміни його рівнів є збільшення інтервалів (періодів) часу. Суть цього методу полягає в тому, що дані динамічного ряду поєднують в групи за періодами, обчислюють середній показник за деякий період – три роки, п’ять років тощо. Збільшення інтервалів проілюструємо на прикладі врожайності озимої пшениці (табл. 11.3). Таблиця 11.3 Зведені дані динамічного ряду до середнього показника за методом збільшення інтервалів часу
В цьому разі збільшують інтервали, наприклад, від одного до трьох років, отримують новий ряд динаміки сумарної врожайності за три роки, який уже показує тенденцію – зростання досліджуваного показника. Тенденція середньої річної врожайності за три роки також відповідає зростанню. · Важливим способом виявлення загальної тенденції ряду динаміки є згладжування за допомогою рухомої середньої. Тут також вдаються до збільшення періодів, але шляхом послідовних зрушень на одну дату при збереженні постійного інтервалу періоду. Таблиця 11.4 Зведені дані динамічного ряду до рухомого середнього показника за методом збільшення інтервалів часу
Згладжений ряд, який складається з рухомих середніх, описує повільніше підвищення врожайності озимої пшениці. · Найефективнішим є складний спосіб виявлення основної тенденції - аналітичне згладжування. На практиці найпоширенішими формулами, які описують тенденцію розвитку (тренд) явищ, є: пряма, гіпербола, парабола другого і третього порядків, показникова функція, ряд Фур’є та деякі інші. · Згладжування за прямою використовують у тих випадках, коли абсолютні прирости більш-менш сталі, тобто коли рівні динамічного ряду змінюються в арифметичній прогресії. Рівняння згладженої прямої динамічного ряду має вигляд:
де а0 і а1 - параметри прямої (початковий рівень і щорічний приріст); t - умовне позначення часу. Для знаходження параметрів “а0” і “а1” потрібно розв’язати за способом найменших квадратів систему нормальних рівнянь:
де y - фактичні рівні динамічного ряду; n - число членів ряду динаміки. Дану систему нормальних рівнянь можна легко спростити, якщо відлік часу брати з середини ряду таким чином, щоб сума часу дорівнювала нулю: У разі відліку часу від середини ряду, коли
Методику згладжування урожайності озимої пшениці за рівнянням прямої покажемо на прикладі (табл. 11.5). Таблиця 10.15.
Поиск по сайту: |
 або
або 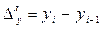
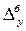 ,
, 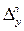 - базисний і ланцюговий абсолютний приріст;
- базисний і ланцюговий абсолютний приріст;


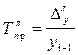 , або
, або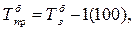
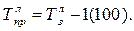
 або
або 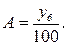
 )
)
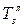 )
)
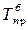 )
)
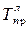 )
)
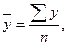
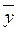 - середній рівень ряду;
- середній рівень ряду; - сума рівнів ряду;
- сума рівнів ряду; млн. т.
млн. т.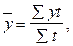
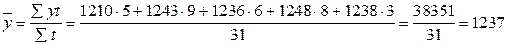 чол.
чол. чол.,
чол.,

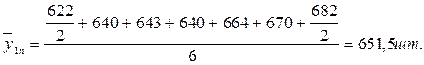 або
або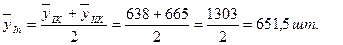
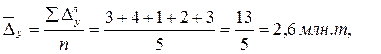 або
або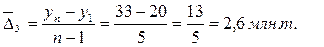
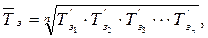
 - ланцюгові темпи зростання;
- ланцюгові темпи зростання;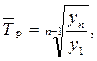
 або
або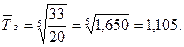
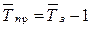 (у вигляді коефіцієнтів);
(у вигляді коефіцієнтів);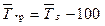 (у вигляді відсотків).
(у вигляді відсотків).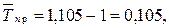 або
або 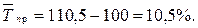
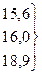
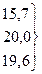
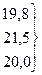

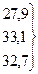
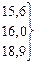 15,7
20,0
19,6
19,8
21,5
20,0
27,3
24,4
28,2
27,9
33,1
32,7
15,7
20,0
19,6
19,8
21,5
20,0
27,3
24,4
28,2
27,9
33,1
32,7
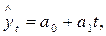
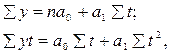
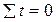 .
.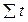 = 0, система рівнянь для знаходження параметрів “а0” і “а1” має такий вигляд:
= 0, система рівнянь для знаходження параметрів “а0” і “а1” має такий вигляд: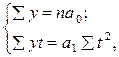 звідки:
звідки: