|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Показники для обчислення коефіцієнтів регресії
Застосувавши метод найменших квадратів, дістанемо систему нормальних рівнянь з трьома невідомими:
Якщо добитись, щоб
Розв’язавши цю систему рівнянь, дістанемо такі значення параметрів: а0 = 0,549; а1 = 0,393; а2 = 0,073. Лінійне рівняння зв’язку матиме вигляд:
Параметри рівняння регресії потрібно тлумачити так: якщо при інших рівних умовах глибина зрошення багаторічних трав з додаванням органічних компонентів збільшиться на 1см, то врожайність насіння цих трав зросте на 0,393 ц/га. За рахунок впливу інших чинників, які рівномірно змінюються протягом часу, врожайність насіння багаторічних трав щорічно зростатиме в середньому на 0,073 ц/га. Підставивши в отримане рівняння регресії значення “t” i “x”, визначимо теоретичні рівні врожайності багаторічних трав (остання колонка табл. 11.14).
і т.д. Наведене рівняння регресії має виключити авторегресію. Аби переконатися в цьому, знайдемо автокореляцію різниць між фактичними і згладженими рівняннями, тобто кореляцію величин Коефіцієнт автокореляції відхилень набирає значення в межах від -1 до +1 і визначається за формулою: Таблиця 11.15
У наведеному прикладі коефіцієнт автокореляції з часовим зсувом-лагом Р = 1 : Значення коефіцієнта додатне, ra = 0,381, свідчить про незначний ступінь кореляції залишкових величин. Висновок щодо наявності або відсутності автокореляції в залишкових величинах роблять, порівнюючи фактичне значення “ra” з табличним для даного числа спостережень “n” і прийнятого рівня значущості. Для наведеного прикладу: raф = 0,381, при n = 10 і 5 %-му рівні ймовірності raт= 0,360. Тобто raф > raТ на 0,021 пункта, що й засвідчує про незначну автокореляцію. У багатьох економіко-статистичних дослідженнях доводиться вивчати паралельно кілька динамічних рядів, в яких коливання рівнів взаємозумовлені. Для вимірювання залежності між такими рядами динаміки використовують методи кореляції, тобто розраховують різні коефіцієнти кореляції. Розглянемо приклад: потрібно виміряти силу зв’язку між рядами динаміки, застосувавши метод кореляції рівнів умовних даних про зміну вартості основних виробничих фондів і випуску продукції за деякі роки. З цією метою скористаємося лінійним коефіцієнтом кореляції, для розрахунку якого побудуємо табл. 11.16. Таблиця 11.16
Поиск по сайту: |



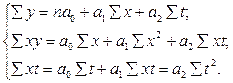
 , то за даними табл. 11.14, система нормальних рівнянь має такий вигляд:
, то за даними табл. 11.14, система нормальних рівнянь має такий вигляд: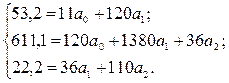


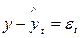 (табл. 11.15).
(табл. 11.15).