 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Центр мас ізольованої системи або нерухомий, або рухається рiвномiрно i прямолiнiйно
Якщо початок вiдлiку помістити в центр мас (система вiдлiку Центр мас є точка простору, відносно якої повний імпульс ізольованої системи дорівнює нулю. РЕАКТИВНИЙ РУХ.
Розглянемо рух тiла зі змінною масою. Мається на увазі не релятивістська залежність маси тiла від швидкостi, оскільки мова йтиме про відносно повільний рух тiл, а зміна маси тiла за рахунок втрати чи поповнення ним речовини. Один з прикладів такого руху - рух ракети. Ракета з великою швидкістю викидає речовину (гази), діючи на неї з великою силою. Речовина, що викидається, з такою ж, але протилежно направленою силою в свою чергу діє на ракету i надає їй прискорення в протилежному напрямі. Якщо зовнiшнiх сил немає, то імпульс системи "ракета - викинута речовина" не змінюється з часом. Розглянемо загальний випадок, коли на ракету діють зовнiшнi сили. Нехай m(t) - маса ракети в довільний момент часу t , а
Розкриємо дужки:
Різниця (Якщо ракету взяти за нерухому СВ то слід вважати що оточуюче середовище рухається зі швидкістю Отже:
Розділимо (2.16) на dt :
За формою (2.17) співпадає з рівнянням другого закону Ньютона. Однак маса тут не постійна, а змінюється з часом. До зовнішньої сили
Якщо маса вiддiляється, то Рiвняння (2.17) i еквівалентне йому рівняння (2.16) називають рівнянням руху точки iз змінною масою або рівнянням Мещерського ( Мещерський I.В. (1859 - 1935)). Якщо
Будемо вважати, що
Значення C визначимо з початкових умов (якщо
Таким чином:
(2.21) називають формулою Ціолковського (К.Е. Ціолковський (1857-1935)). (Застосування (2.21) до польотів космічних ракет дає наступні значення відношень
Поиск по сайту: |
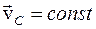 ), то
), то 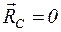 ,
, 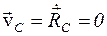 і
і  .
. − її швидкiсть. Імпульс ракети в цей момент часу дорівнює
− її швидкiсть. Імпульс ракети в цей момент часу дорівнює  . Через час dt маса i швидкiсть одержать прирости
. Через час dt маса i швидкiсть одержать прирости 
 i
i  . Імпульс ракети тепер дорівнює
. Імпульс ракети тепер дорівнює  . Імпульс газів, що утворилися за цей же час dt, дорівнює
. Імпульс газів, що утворилися за цей же час dt, дорівнює 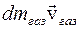 , де
, де  − маса газів,
− маса газів,  − їх швидкiсть. Приріст iмпульсу ракети дорівнює iмпульсу рiвнодiйної зовнiшнiх сил (див. (2.12)):
− їх швидкiсть. Приріст iмпульсу ракети дорівнює iмпульсу рiвнодiйної зовнiшнiх сил (див. (2.12)): .
.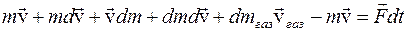 .
. Оскільки dt − нескінченно мала величина (dt
Оскільки dt − нескінченно мала величина (dt  0), то
0), то  − нескінченно мала величина вищого порядку i її можна відкинути;
− нескінченно мала величина вищого порядку i її можна відкинути; 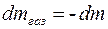 згідно закону збереження маси. Після перетворень одержимо:
згідно закону збереження маси. Після перетворень одержимо: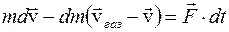
 − це швидкiсть витікання газів відносно ракети; її називають швидкістю газової струмини (див.рис.2.3).
− це швидкiсть витікання газів відносно ракети; її називають швидкістю газової струмини (див.рис.2.3).
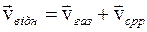 ;
; 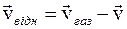 ).
).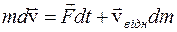
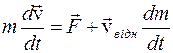
 додається член
додається член  , який носить назву реактивної сили:
, який носить назву реактивної сили:
 < 0 i вектор
< 0 i вектор  протилежний вектору
протилежний вектору  ; якщо маса приєднується, то
; якщо маса приєднується, то 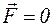 , то з (2.16) одержимо:
, то з (2.16) одержимо: .
. Нехай ракета рухається в напрямку, протилежному
Нехай ракета рухається в напрямку, протилежному  ;
;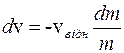
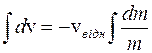
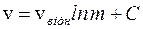
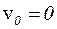 , то початкова маса дорівнює
, то початкова маса дорівнює  ), які підставимо в (2.20):
), які підставимо в (2.20): , звідки
, звідки 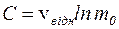 .
.
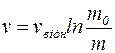 , або
, або  . Остаточно:
. Остаточно: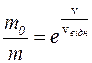
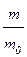 . При vвідн=1 км/c для v1=8 км/c матимемо
. При vвідн=1 км/c для v1=8 км/c матимемо  що нереально (потрібні кращі сорти палива). При vвідн=4 км/c
що нереально (потрібні кращі сорти палива). При vвідн=4 км/c  (політ в одну сторону)).
(політ в одну сторону)).